Efficient Deep Neural Receiver with Post-Training Quantization

Deep learning has recently garnered significant interest in wireless communications due to its superior performance compared to traditional model-based algorithms. Deep convolutional neural networks (CNNs) have demonstrated notable improvements in block error rate (BLER) under various channel models and mobility scenarios. However, the high computational complexity and resource demands of deep CNNs pose challenges for deployment in resource-constrained edge systems. The 3rd Generation Partnership Project (3GPP) Release 20 highlights the pivotal role of artificial intelligence (AI) integration in enabling advanced radio-access networks for 6G systems. The hard real-time processing demands of 5G and 6G require efficient techniques such as post-training quantization (PTQ), quantization-aware training (QAT), pruning, and hybrid approaches to meet latency requirements. In this paper, we focus on PTQ to reduce model complexity by lowering the bit-width of weights, thereby enhancing computational efficiency. Our analysis employs symmetric uniform quantization, applying both per-tensor and per-channel PTQ to a neural receiver achieving performance comparable to full-precision models. Specifically, 8-bit per-channel quantization maintains BLER performance with minimal degradation, while 4-bit quantization shows great promise but requires further optimization to achieve target BLER levels. These results highlight the potential of ultra-low bitwidth PTQ for efficient neural receiver deployment in 6G systems.

Robust Activity Detection for Massive Random Access

Massive machine-type communications (mMTC) are fundamental to the Internet of Things (IoT) framework in future wireless networks, involving the connection of a vast number of devices with sporadic transmission patterns. Traditional device activity detection (AD) methods are typically developed for Gaussian noise, but their performance may deteriorate when these conditions are not met, particularly in the presence of heavy-tailed impulsive noise. In this paper, we propose robust statistical techniques for AD that do not rely on the Gaussian assumption and replace the Gaussian loss function with robust loss functions that can effectively mitigate the impact of heavy-tailed noise and outliers. First, we prove that the coordinate-wise (conditional) objective function is geodesically convex and derive a fixed-point (FP) algorithm for minimizing it, along with convergence guarantees. Building on the FP algorithm, we propose two robust algorithms for solving the full (unconditional) objective function: a coordinate-wise optimization algorithm (RCWO) and a greedy covariance learning-based matching pursuit algorithm (RCL-MP). Numerical experiments demonstrate that the proposed methods significantly outperform existing algorithms in scenarios with non-Gaussian noise, achieving higher detection accuracy and robustness.

AI-Empowered Integrated Sensing and Communications

Integrating sensing and communication (ISAC) can help overcome the challenges of limited spectrum and expensive hardware, leading to improved energy and cost efficiency. While full cooperation between sensing and communication can result in significant performance gains, achieving optimal performance requires efficient designs of unified waveforms and beamformers for joint sensing and communication. Sophisticated statistical signal processing and multi-objective optimization techniques are necessary to balance the competing design requirements of joint sensing and communication tasks. Since model-based analytical approaches may be suboptimal or overly complex, deep learning emerges as a powerful tool for developing data-driven signal processing algorithms, particularly when optimal algorithms are unknown or when known algorithms are too complex for real-time implementation. Unified waveform and beamformer design problems for ISAC fall into this category, where fundamental design trade-offs exist between sensing and communication performance metrics, and the underlying models may be inadequate or incomplete. This article explores the application of artificial intelligence (AI) in ISAC designs to enhance efficiency and reduce complexity. We emphasize the integration benefits through AI-driven ISAC designs, prioritizing the development of unified waveforms, constellations, and beamforming strategies for both sensing and communication. To illustrate the practical potential of AI-driven ISAC, we present two case studies on waveform and beamforming design, demonstrating how unsupervised learning and neural network-based optimization can effectively balance performance, complexity, and implementation constraints.

Activity Detection for Massive Random Access using Covariance-based Matching Pursuit

The Internet of Things paradigm heavily relies on a network of a massive number of machine-type devices (MTDs) that monitor changes in various phenomena. Consequently, MTDs are randomly activated at different times whenever a change occurs. This essentially results in relatively few MTDs being active simultaneously compared to the entire network, resembling targeted sampling in compressed sensing. Therefore, signal recovery in machine-type communications is addressed through joint user activity detection and channel estimation algorithms built using compressed sensing theory. However, most of these algorithms follow a two-stage procedure in which a channel is first estimated and later mapped to find active users. This approach is inefficient because the estimated channel information is subsequently discarded. To overcome this limitation, we introduce a novel covariance-learning matching pursuit algorithm that bypasses explicit channel estimation. Instead, it focuses on estimating the indices of the active users greedily. Simulation results presented in terms of probability of miss detection, exact recovery rate, and computational complexity validate the proposed technique's superior performance and efficiency.

Regularized EM algorithm

Expectation-Maximization (EM) algorithm is a widely used iterative algorithm for computing (local) maximum likelihood estimate (MLE). It can be used in an extensive range of problems, including the clustering of data based on the Gaussian mixture model (GMM). Numerical instability and convergence problems may arise in situations where the sample size is not much larger than the data dimensionality. In such low sample support (LSS) settings, the covariance matrix update in the EM-GMM algorithm may become singular or poorly conditioned, causing the algorithm to crash. On the other hand, in many signal processing problems, a priori information can be available indicating certain structures for different cluster covariance matrices. In this paper, we present a regularized EM algorithm for GMM-s that can make efficient use of such prior knowledge as well as cope with LSS situations. The method aims to maximize a penalized GMM likelihood where regularized estimation may be used to ensure positive definiteness of covariance matrix updates and shrink the estimators towards some structured target covariance matrices. We show that the theoretical guarantees of convergence hold, leading to better performing EM algorithm for structured covariance matrix models or with low sample settings.

Graph Neural Network Sensitivity Under Probabilistic Error Model

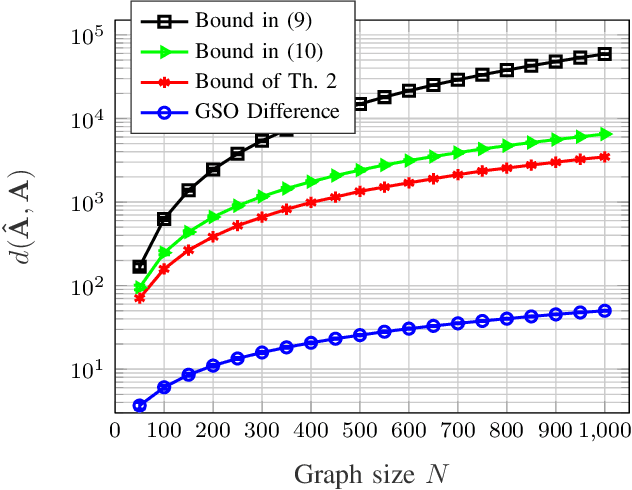
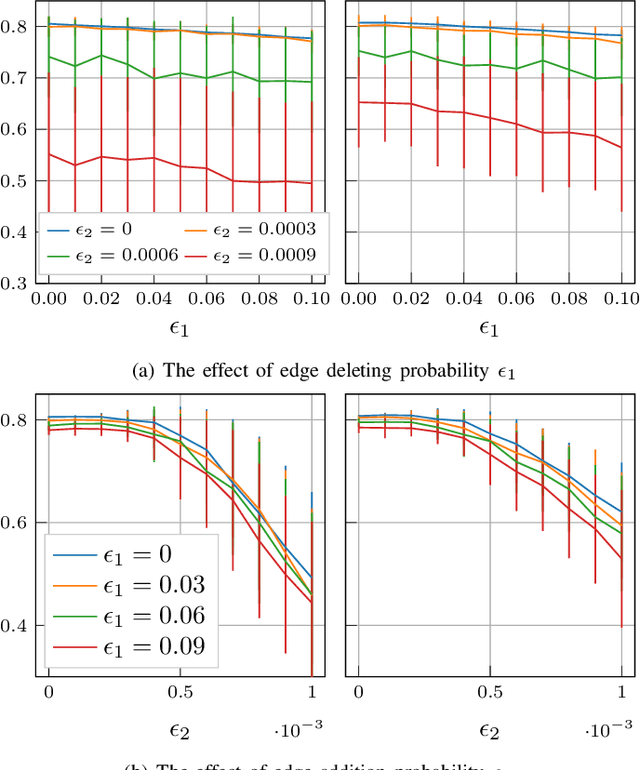
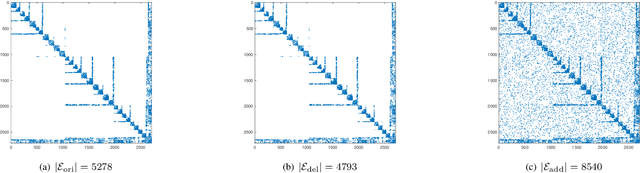
Graph convolutional networks (GCNs) can successfully learn the graph signal representation by graph convolution. The graph convolution depends on the graph filter, which contains the topological dependency of data and propagates data features. However, the estimation errors in the propagation matrix (e.g., the adjacency matrix) can have a significant impact on graph filters and GCNs. In this paper, we study the effect of a probabilistic graph error model on the performance of the GCNs. We prove that the adjacency matrix under the error model is bounded by a function of graph size and error probability. We further analytically specify the upper bound of a normalized adjacency matrix with self-loop added. Finally, we illustrate the error bounds by running experiments on a synthetic dataset and study the sensitivity of a simple GCN under this probabilistic error model on accuracy.

Coupled Feature Learning for Multimodal Medical Image Fusion

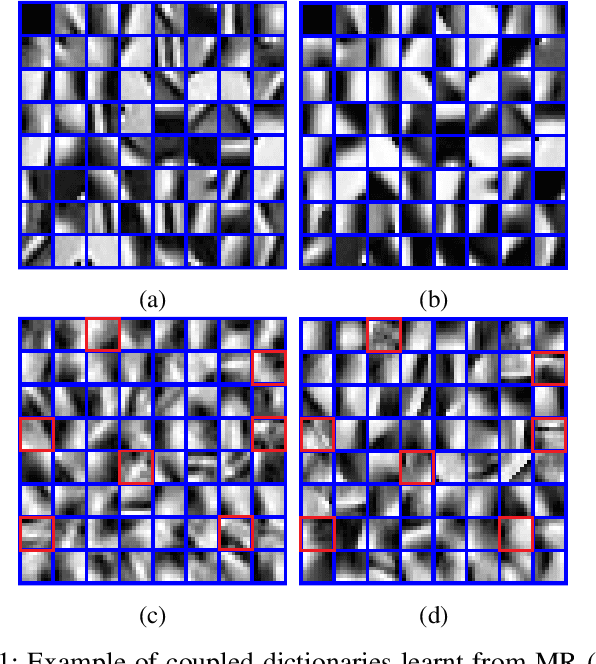
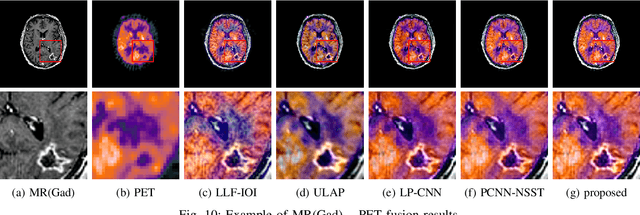
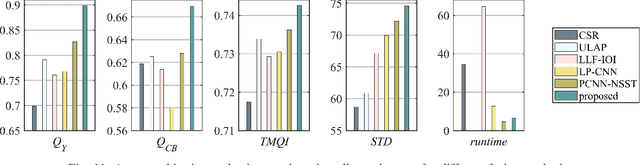
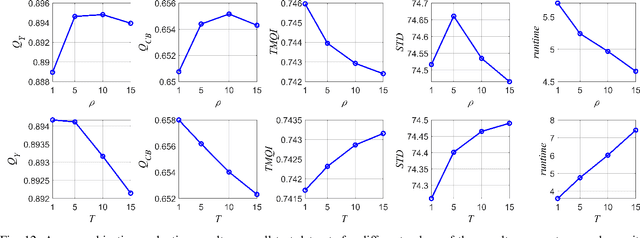
Multimodal image fusion aims to combine relevant information from images acquired with different sensors. In medical imaging, fused images play an essential role in both standard and automated diagnosis. In this paper, we propose a novel multimodal image fusion method based on coupled dictionary learning. The proposed method is general and can be employed for different medical imaging modalities. Unlike many current medical fusion methods, the proposed approach does not suffer from intensity attenuation nor loss of critical information. Specifically, the images to be fused are decomposed into coupled and independent components estimated using sparse representations with identical supports and a Pearson correlation constraint, respectively. An alternating minimization algorithm is designed to solve the resulting optimization problem. The final fusion step uses the max-absolute-value rule. Experiments are conducted using various pairs of multimodal inputs, including real MR-CT and MR-PET images. The resulting performance and execution times show the competitiveness of the proposed method in comparison with state-of-the-art medical image fusion methods.

Coupled regularized sample covariance matrix estimator for multiple classes

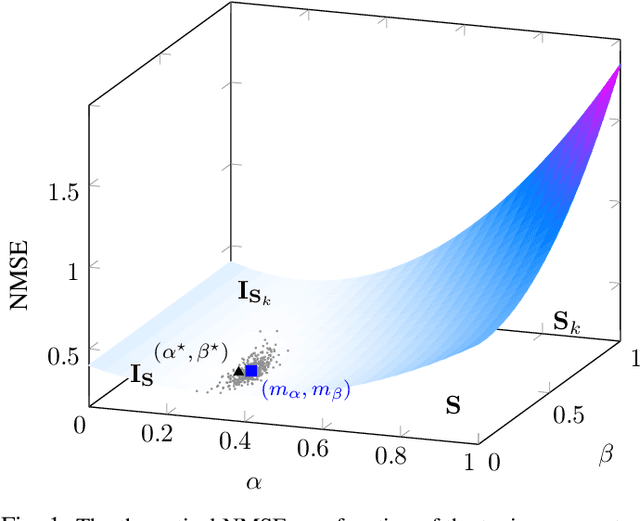
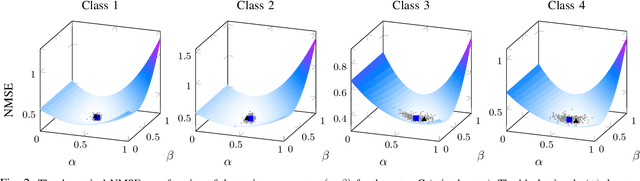
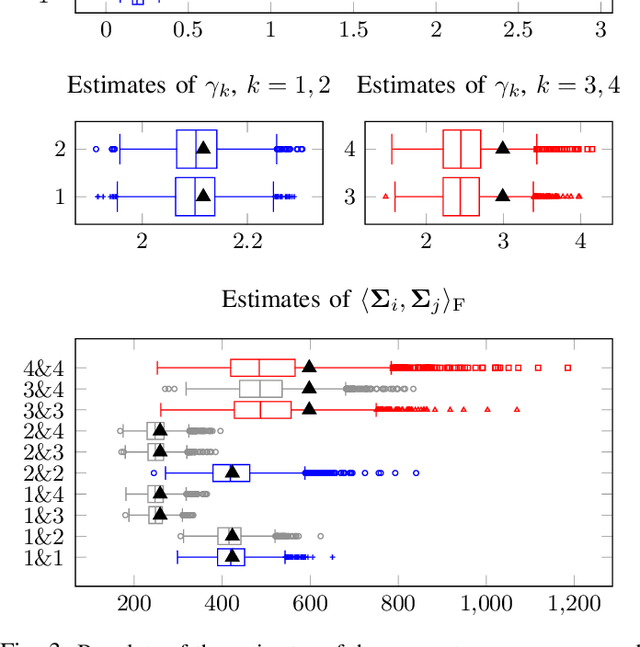
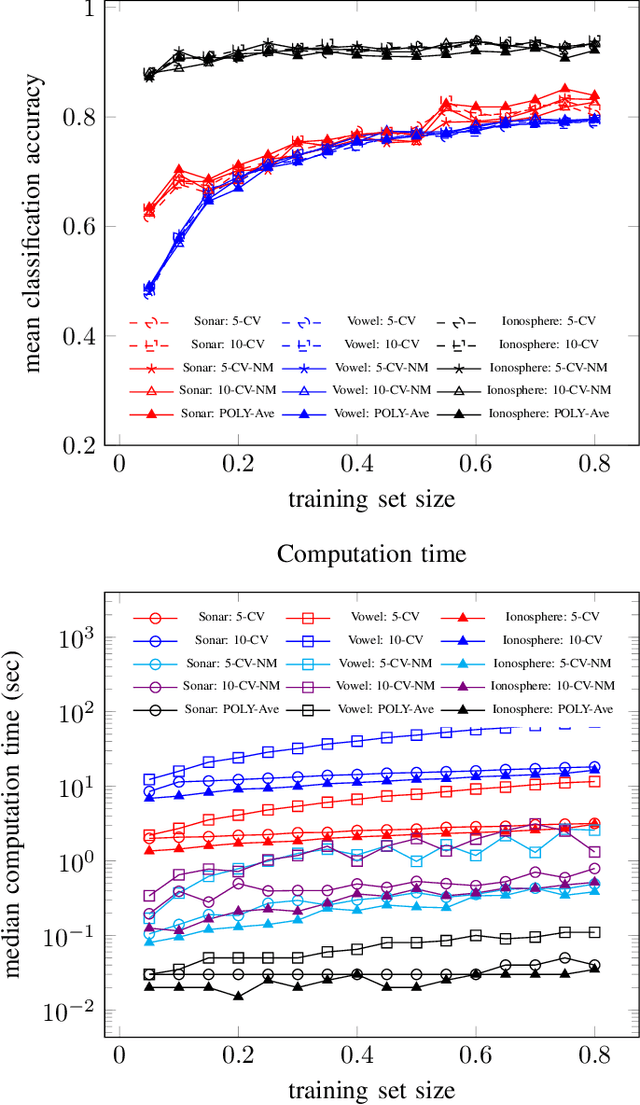
The estimation of covariance matrices of multiple classes with limited training data is a difficult problem. The sample covariance matrix (SCM) is known to perform poorly when the number of variables is large compared to the available number of samples. In order to reduce the mean squared error (MSE) of the SCM, regularized (shrinkage) SCM estimators are often used. In this work, we consider regularized SCM (RSCM) estimators for multiclass problems that couple together two different target matrices for regularization: the pooled (average) SCM of the classes and the scaled identity matrix. Regularization toward the pooled SCM is beneficial when the population covariances are similar, whereas regularization toward the identity matrix guarantees that the estimators are positive definite. We derive the MSE optimal tuning parameters for the estimators as well as propose a method for their estimation under the assumption that the class populations follow (unspecified) elliptical distributions with finite fourth-order moments. The MSE performance of the proposed coupled RSCMs are evaluated with simulations and in a regularized discriminant analysis (RDA) classification set-up on real data. The results based on three different real data sets indicate comparable performance to cross-validation but with a significant speed-up in computation time.

Block-wise Minimization-Majorization algorithm for Huber's criterion: sparse learning and applications

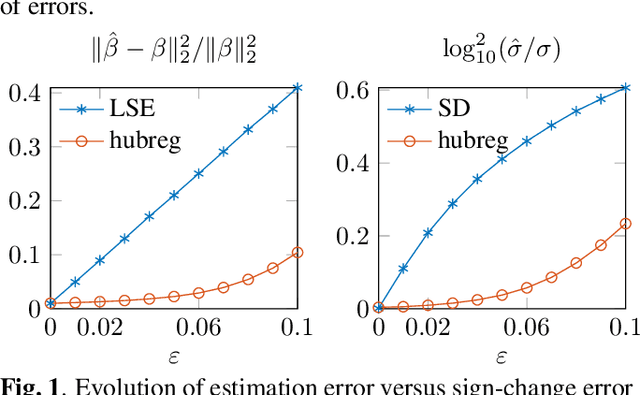
Huber's criterion can be used for robust joint estimation of regression and scale parameters in the linear model. Huber's (Huber, 1981) motivation for introducing the criterion stemmed from non-convexity of the joint maximum likelihood objective function as well as non-robustness (unbounded influence function) of the associated ML-estimate of scale. In this paper, we illustrate how the original algorithm proposed by Huber can be set within the block-wise minimization majorization framework. In addition, we propose novel data-adaptive step sizes for both the location and scale, which are further improving the convergence. We then illustrate how Huber's criterion can be used for sparse learning of underdetermined linear model using the iterative hard thresholding approach. We illustrate the usefulness of the algorithms in an image denoising application and simulation studies.

A Compressive Classification Framework for High-Dimensional Data

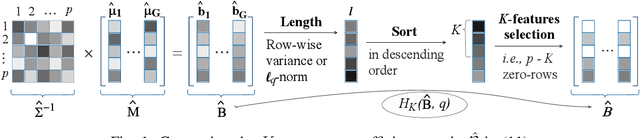
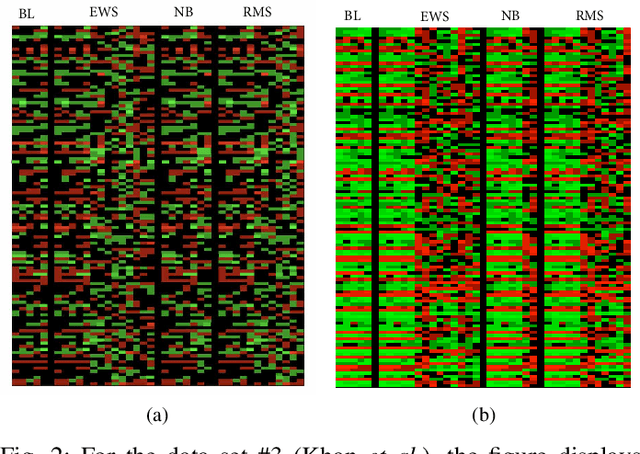
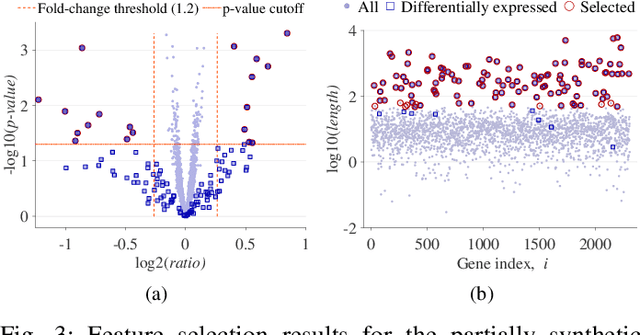
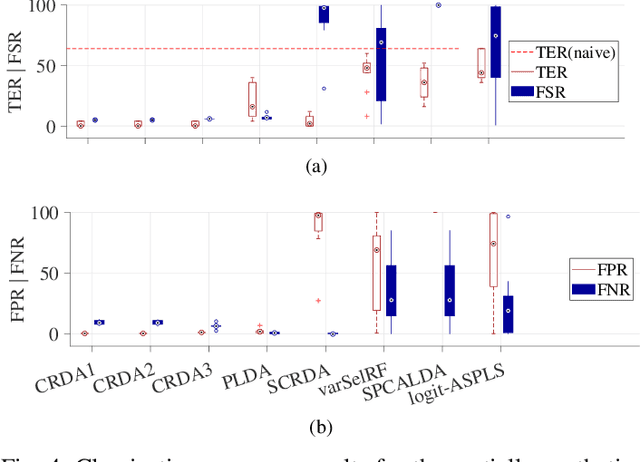
We propose a compressive classification framework for settings where the data dimensionality is significantly higher than the sample size. The proposed method, referred to as compressive regularized discriminant analysis (CRDA) is based on linear discriminant analysis and has the ability to select significant features by using joint-sparsity promoting hard thresholding in the discriminant rule. Since the number of features is larger than the sample size, the method also uses state-of-the-art regularized sample covariance matrix estimators. Several analysis examples on real data sets, including image, speech signal and gene expression data illustrate the promising improvements offered by the proposed CRDA classifier in practise. Overall, the proposed method gives fewer misclassification errors than its competitors, while at the same time achieving accurate feature selection results. The open-source R package and MATLAB toolbox of the proposed method (named compressiveRDA) is freely available.