Robust Activity Detection for Massive Random Access

Massive machine-type communications (mMTC) are fundamental to the Internet of Things (IoT) framework in future wireless networks, involving the connection of a vast number of devices with sporadic transmission patterns. Traditional device activity detection (AD) methods are typically developed for Gaussian noise, but their performance may deteriorate when these conditions are not met, particularly in the presence of heavy-tailed impulsive noise. In this paper, we propose robust statistical techniques for AD that do not rely on the Gaussian assumption and replace the Gaussian loss function with robust loss functions that can effectively mitigate the impact of heavy-tailed noise and outliers. First, we prove that the coordinate-wise (conditional) objective function is geodesically convex and derive a fixed-point (FP) algorithm for minimizing it, along with convergence guarantees. Building on the FP algorithm, we propose two robust algorithms for solving the full (unconditional) objective function: a coordinate-wise optimization algorithm (RCWO) and a greedy covariance learning-based matching pursuit algorithm (RCL-MP). Numerical experiments demonstrate that the proposed methods significantly outperform existing algorithms in scenarios with non-Gaussian noise, achieving higher detection accuracy and robustness.

Graph Neural Network Sensitivity Under Probabilistic Error Model

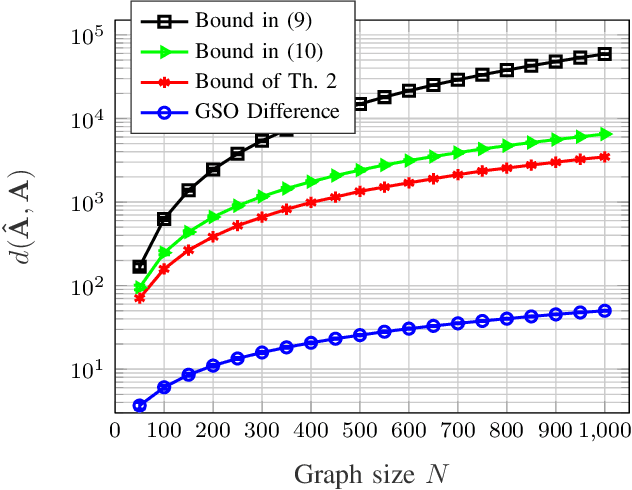
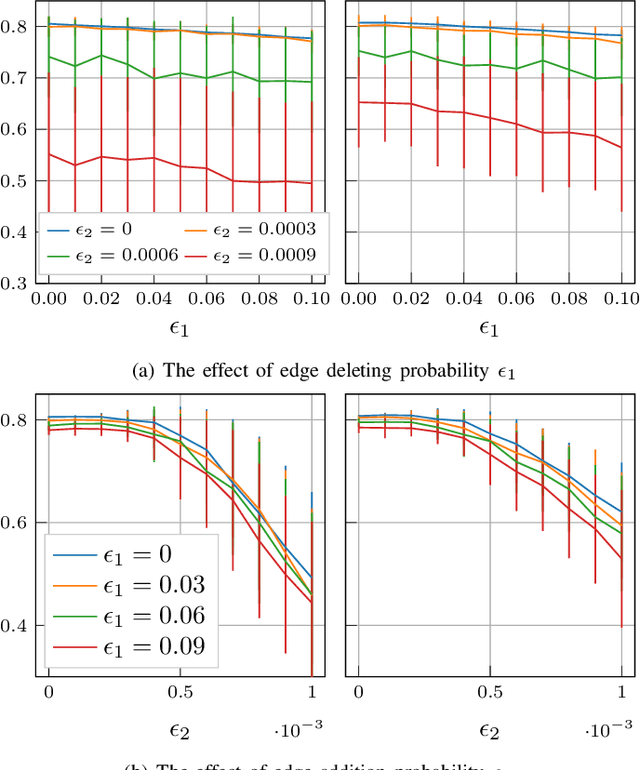
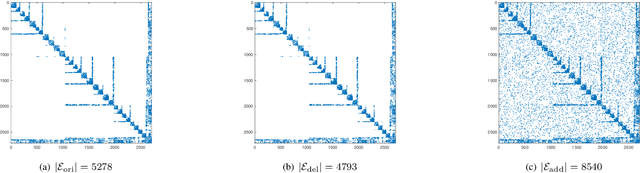
Graph convolutional networks (GCNs) can successfully learn the graph signal representation by graph convolution. The graph convolution depends on the graph filter, which contains the topological dependency of data and propagates data features. However, the estimation errors in the propagation matrix (e.g., the adjacency matrix) can have a significant impact on graph filters and GCNs. In this paper, we study the effect of a probabilistic graph error model on the performance of the GCNs. We prove that the adjacency matrix under the error model is bounded by a function of graph size and error probability. We further analytically specify the upper bound of a normalized adjacency matrix with self-loop added. Finally, we illustrate the error bounds by running experiments on a synthetic dataset and study the sensitivity of a simple GCN under this probabilistic error model on accuracy.