Navigating Demand Uncertainty in Container Shipping: Deep Reinforcement Learning for Enabling Adaptive and Feasible Master Stowage Planning

Reinforcement learning (RL) has shown promise in solving various combinatorial optimization problems. However, conventional RL faces challenges when dealing with real-world constraints, especially when action space feasibility is explicit and dependent on the corresponding state or trajectory. In this work, we focus on using RL in container shipping, often considered the cornerstone of global trade, by dealing with the critical challenge of master stowage planning. The main objective is to maximize cargo revenue and minimize operational costs while navigating demand uncertainty and various complex operational constraints, namely vessel capacity and stability, which must be dynamically updated along the vessel's voyage. To address this problem, we implement a deep reinforcement learning framework with feasibility projection to solve the master stowage planning problem (MPP) under demand uncertainty. The experimental results show that our architecture efficiently finds adaptive, feasible solutions for this multi-stage stochastic optimization problem, outperforming traditional mixed-integer programming and RL with feasibility regularization. Our AI-driven decision-support policy enables adaptive and feasible planning under uncertainty, optimizing operational efficiency and capacity utilization while contributing to sustainable and resilient global supply chains.

Fair Resource Allocation in Weakly Coupled Markov Decision Processes

We consider fair resource allocation in sequential decision-making environments modeled as weakly coupled Markov decision processes, where resource constraints couple the action spaces of $N$ sub-Markov decision processes (sub-MDPs) that would otherwise operate independently. We adopt a fairness definition using the generalized Gini function instead of the traditional utilitarian (total-sum) objective. After introducing a general but computationally prohibitive solution scheme based on linear programming, we focus on the homogeneous case where all sub-MDPs are identical. For this case, we show for the first time that the problem reduces to optimizing the utilitarian objective over the class of "permutation invariant" policies. This result is particularly useful as we can exploit Whittle index policies in the restless bandits setting while, for the more general setting, we introduce a count-proportion-based deep reinforcement learning approach. Finally, we validate our theoretical findings with comprehensive experiments, confirming the effectiveness of our proposed method in achieving fairness.

Q-learning for Quantile MDPs: A Decomposition, Performance, and Convergence Analysis

In Markov decision processes (MDPs), quantile risk measures such as Value-at-Risk are a standard metric for modeling RL agents' preferences for certain outcomes. This paper proposes a new Q-learning algorithm for quantile optimization in MDPs with strong convergence and performance guarantees. The algorithm leverages a new, simple dynamic program (DP) decomposition for quantile MDPs. Compared with prior work, our DP decomposition requires neither known transition probabilities nor solving complex saddle point equations and serves as a suitable foundation for other model-free RL algorithms. Our numerical results in tabular domains show that our Q-learning algorithm converges to its DP variant and outperforms earlier algorithms.

Planning and Learning in Risk-Aware Restless Multi-Arm Bandit Problem

In restless multi-arm bandits, a central agent is tasked with optimally distributing limited resources across several bandits (arms), with each arm being a Markov decision process. In this work, we generalize the traditional restless multi-arm bandit problem with a risk-neutral objective by incorporating risk-awareness. We establish indexability conditions for the case of a risk-aware objective and provide a solution based on Whittle index. In addition, we address the learning problem when the true transition probabilities are unknown by proposing a Thompson sampling approach and show that it achieves bounded regret that scales sublinearly with the number of episodes and quadratically with the number of arms. The efficacy of our method in reducing risk exposure in restless multi-arm bandits is illustrated through a set of numerical experiments.

Data-driven decision-making under uncertainty with entropic risk measure

The entropic risk measure is widely used in high-stakes decision making to account for tail risks associated with an uncertain loss. With limited data, the empirical entropic risk estimator, i.e. replacing the expectation in the entropic risk measure with a sample average, underestimates the true risk. To debias the empirical entropic risk estimator, we propose a strongly asymptotically consistent bootstrapping procedure. The first step of the procedure involves fitting a distribution to the data, whereas the second step estimates the bias of the empirical entropic risk estimator using bootstrapping, and corrects for it. We show that naively fitting a Gaussian Mixture Model to the data using the maximum likelihood criterion typically leads to an underestimation of the risk. To mitigate this issue, we consider two alternative methods: a more computationally demanding one that fits the distribution of empirical entropic risk, and a simpler one that fits the extreme value distribution. As an application of the approach, we study a distributionally robust entropic risk minimization problem with type-$\infty$ Wasserstein ambiguity set, where debiasing the validation performance using our techniques significantly improves the calibration of the size of the ambiguity set. Furthermore, we propose a distributionally robust optimization model for a well-studied insurance contract design problem. The model considers multiple (potential) policyholders that have dependent risks and the insurer and policyholders use entropic risk measure. We show that cross validation methods can result in significantly higher out-of-sample risk for the insurer if the bias in validation performance is not corrected for. This improvement can be explained from the observation that our methods suggest a higher (and more accurate) premium to homeowners.

End-to-end Conditional Robust Optimization

The field of Contextual Optimization (CO) integrates machine learning and optimization to solve decision making problems under uncertainty. Recently, a risk sensitive variant of CO, known as Conditional Robust Optimization (CRO), combines uncertainty quantification with robust optimization in order to promote safety and reliability in high stake applications. Exploiting modern differentiable optimization methods, we propose a novel end-to-end approach to train a CRO model in a way that accounts for both the empirical risk of the prescribed decisions and the quality of conditional coverage of the contextual uncertainty set that supports them. While guarantees of success for the latter objective are impossible to obtain from the point of view of conformal prediction theory, high quality conditional coverage is achieved empirically by ingeniously employing a logistic regression differentiable layer within the calculation of coverage quality in our training loss. We show that the proposed training algorithms produce decisions that outperform the traditional estimate then optimize approaches.

A Survey of Contextual Optimization Methods for Decision Making under Uncertainty

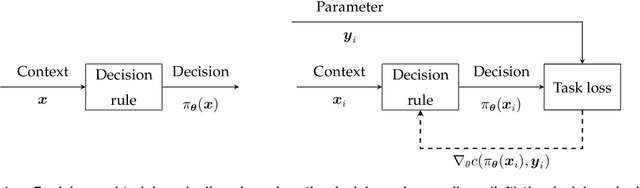
Recently there has been a surge of interest in operations research (OR) and the machine learning (ML) community in combining prediction algorithms and optimization techniques to solve decision-making problems in the face of uncertainty. This gave rise to the field of contextual optimization, under which data-driven procedures are developed to prescribe actions to the decision-maker that make the best use of the most recently updated information. A large variety of models and methods have been presented in both OR and ML literature under a variety of names, including data-driven optimization, prescriptive optimization, predictive stochastic programming, policy optimization, (smart) predict/estimate-then-optimize, decision-focused learning, (task-based) end-to-end learning/forecasting/optimization, etc. Focusing on single and two-stage stochastic programming problems, this review article identifies three main frameworks for learning policies from data and discusses their strengths and limitations. We present the existing models and methods under a uniform notation and terminology and classify them according to the three main frameworks identified. Our objective with this survey is to both strengthen the general understanding of this active field of research and stimulate further theoretical and algorithmic advancements in integrating ML and stochastic programming.

Robust Data-driven Prescriptiveness Optimization

The abundance of data has led to the emergence of a variety of optimization techniques that attempt to leverage available side information to provide more anticipative decisions. The wide range of methods and contexts of application have motivated the design of a universal unitless measure of performance known as the coefficient of prescriptiveness. This coefficient was designed to quantify both the quality of contextual decisions compared to a reference one and the prescriptive power of side information. To identify policies that maximize the former in a data-driven context, this paper introduces a distributionally robust contextual optimization model where the coefficient of prescriptiveness substitutes for the classical empirical risk minimization objective. We present a bisection algorithm to solve this model, which relies on solving a series of linear programs when the distributional ambiguity set has an appropriate nested form and polyhedral structure. Studying a contextual shortest path problem, we evaluate the robustness of the resulting policies against alternative methods when the out-of-sample dataset is subject to varying amounts of distribution shift.

On Dynamic Program Decompositions of Static Risk Measures

Optimizing static risk-averse objectives in Markov decision processes is challenging because they do not readily admit dynamic programming decompositions. Prior work has proposed to use a dynamic decomposition of risk measures that help to formulate dynamic programs on an augmented state space. This paper shows that several existing decompositions are inherently inexact, contradicting several claims in the literature. In particular, we give examples that show that popular decompositions for CVaR and EVaR risk measures are strict overestimates of the true risk values. However, an exact decomposition is possible for VaR, and we give a simple proof that illustrates the fundamental difference between VaR and CVaR dynamic programming properties.

Risk-Aware Bid Optimization for Online Display Advertisement

This research focuses on the bid optimization problem in the real-time bidding setting for online display advertisements, where an advertiser, or the advertiser's agent, has access to the features of the website visitor and the type of ad slots, to decide the optimal bid prices given a predetermined total advertisement budget. We propose a risk-aware data-driven bid optimization model that maximizes the expected profit for the advertiser by exploiting historical data to design upfront a bidding policy, mapping the type of advertisement opportunity to a bid price, and accounting for the risk of violating the budget constraint during a given period of time. After employing a Lagrangian relaxation, we derive a parametrized closed-form expression for the optimal bidding strategy. Using a real-world dataset, we demonstrate that our risk-averse method can effectively control the risk of overspending the budget while achieving a competitive level of profit compared with the risk-neutral model and a state-of-the-art data-driven risk-aware bidding approach.