Multi-Constitutive Neural Network for Large Deformation Poromechanics Problem

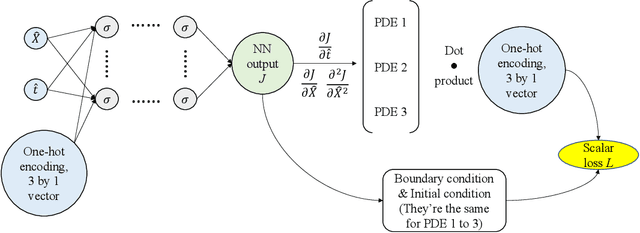
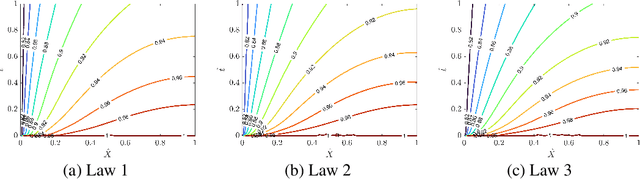
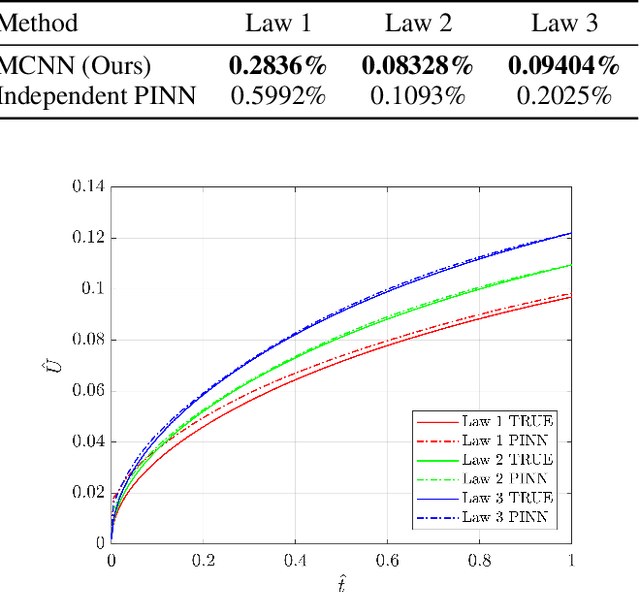
In this paper, we study the problem of large-strain consolidation in poromechanics with deep neural networks. Given different material properties and different loading conditions, the goal is to predict pore pressure and settlement. We propose a novel method "multi-constitutive neural network" (MCNN) such that one model can solve several different constitutive laws. We introduce a one-hot encoding vector as an additional input vector, which is used to label the constitutive law we wish to solve. Then we build a DNN which takes as input (X, t) along with a constitutive model label and outputs the corresponding solution. It is the first time, to our knowledge, that we can evaluate multi-constitutive laws through only one training process while still obtaining good accuracies. We found that MCNN trained to solve multiple PDEs outperforms individual neural network solvers trained with PDE.

Anomaly Detection with Domain Adaptation

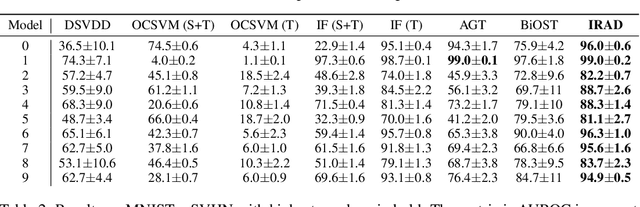
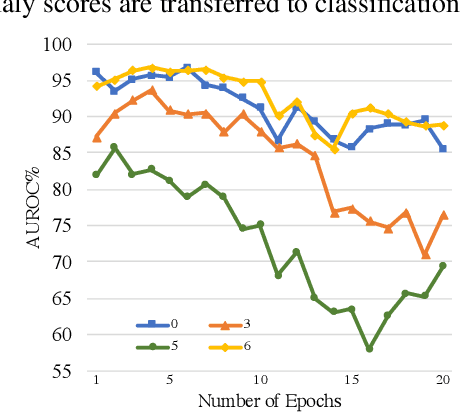
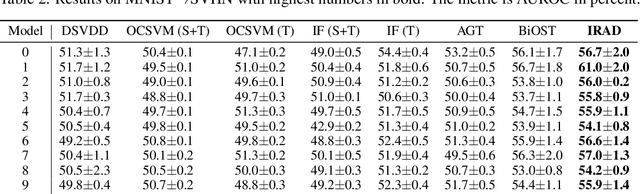
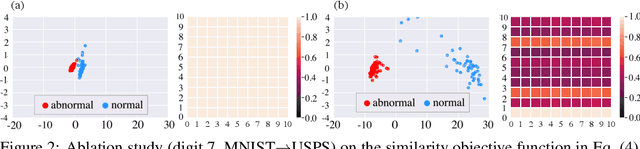
We study the problem of semi-supervised anomaly detection with domain adaptation. Given a set of normal data from a source domain and a limited amount of normal examples from a target domain, the goal is to have a well-performing anomaly detector in the target domain. We propose the Invariant Representation Anomaly Detection (IRAD) to solve this problem where we first learn to extract a domain-invariant representation. The extraction is achieved by an across-domain encoder trained together with source-specific encoders and generators by adversarial learning. An anomaly detector is then trained using the learnt representations. We evaluate IRAD extensively on digits images datasets (MNIST, USPS and SVHN) and object recognition datasets (Office-Home). Experimental results show that IRAD outperforms baseline models by a wide margin across different datasets. We derive a theoretical lower bound for the joint error that explains the performance decay from overtraining and also an upper bound for the generalization error.

Memory Augmented Generative Adversarial Networks for Anomaly Detection

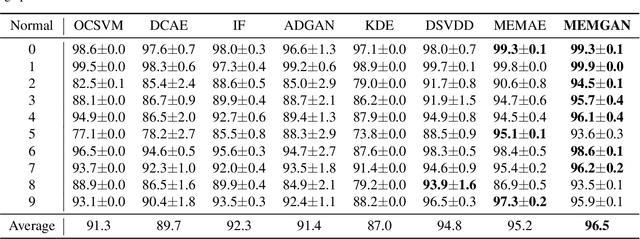
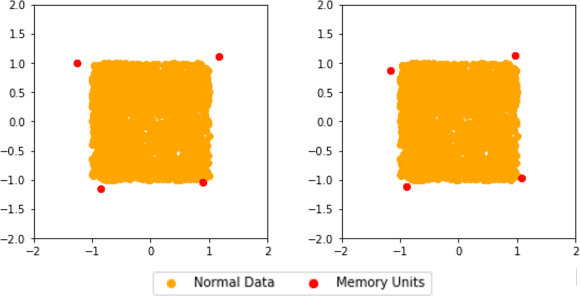
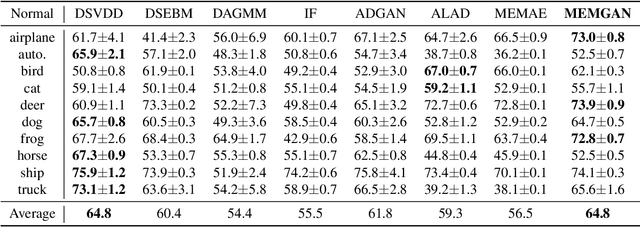
In this paper, we present a memory-augmented algorithm for anomaly detection. Classical anomaly detection algorithms focus on learning to model and generate normal data, but typically guarantees for detecting anomalous data are weak. The proposed Memory Augmented Generative Adversarial Networks (MEMGAN) interacts with a memory module for both the encoding and generation processes. Our algorithm is such that most of the \textit{encoded} normal data are inside the convex hull of the memory units, while the abnormal data are isolated outside. Such a remarkable property leads to good (resp.\ poor) reconstruction for normal (resp.\ abnormal) data and therefore provides a strong guarantee for anomaly detection. Decoded memory units in MEMGAN are more interpretable and disentangled than previous methods, which further demonstrates the effectiveness of the memory mechanism. Experimental results on twenty anomaly detection datasets of CIFAR-10 and MNIST show that MEMGAN demonstrates significant improvements over previous anomaly detection methods.

Regularized Cycle Consistent Generative Adversarial Network for Anomaly Detection

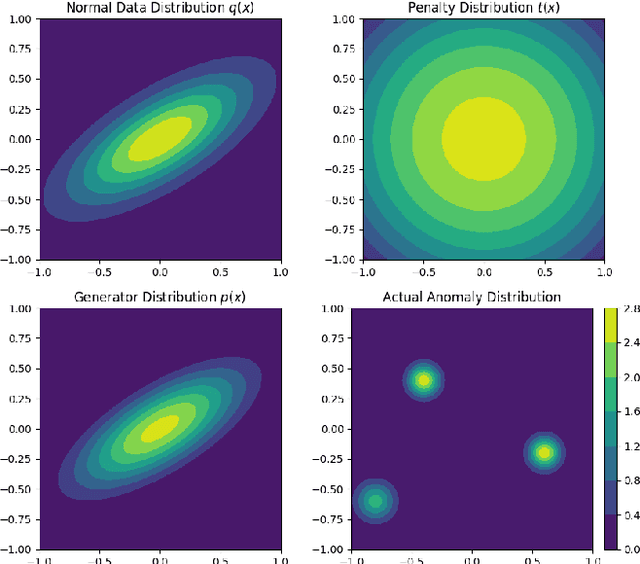
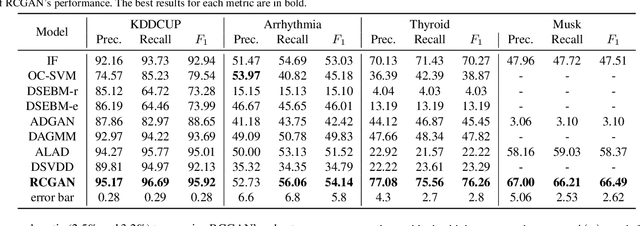
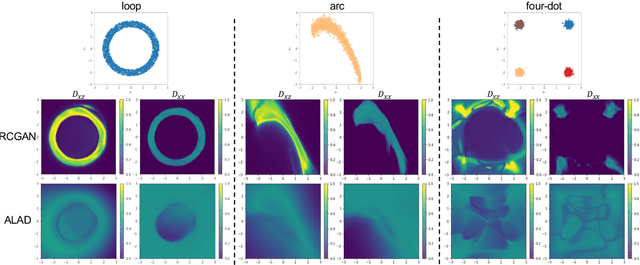
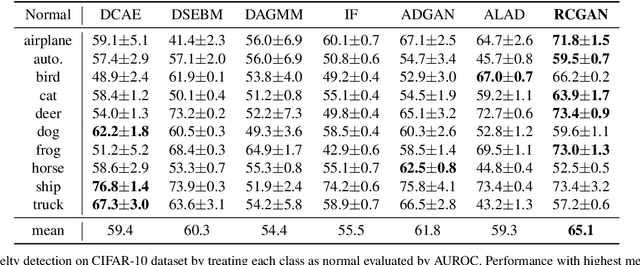
In this paper, we investigate algorithms for anomaly detection. Previous anomaly detection methods focus on modeling the distribution of non-anomalous data provided during training. However, this does not necessarily ensure the correct detection of anomalous data. We propose a new Regularized Cycle Consistent Generative Adversarial Network (RCGAN) in which deep neural networks are adversarially trained to better recognize anomalous samples. This approach is based on leveraging a penalty distribution with a new definition of the loss function and novel use of discriminator networks. It is based on a solid mathematical foundation, and proofs show that our approach has stronger guarantees for detecting anomalous examples compared to the current state-of-the-art. Experimental results on both real-world and synthetic data show that our model leads to significant and consistent improvements on previous anomaly detection benchmarks. Notably, RCGAN improves on the state-of-the-art on the KDDCUP, Arrhythmia, Thyroid, Musk and CIFAR10 datasets.

TED: A Pretrained Unsupervised Summarization Model with Theme Modeling and Denoising

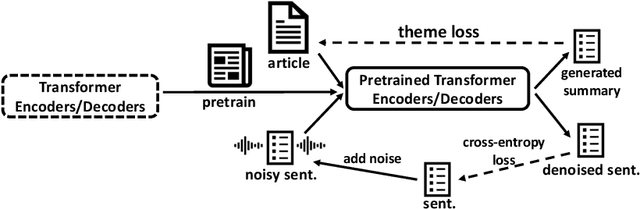
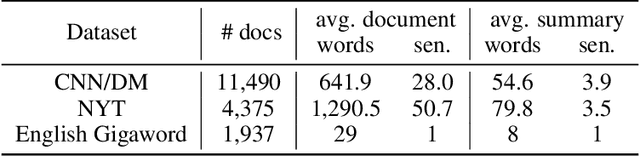
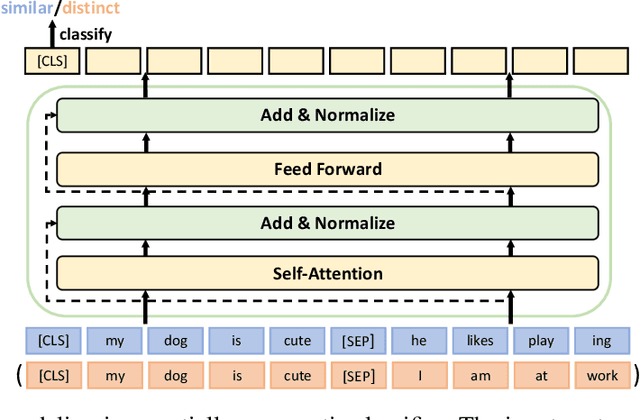
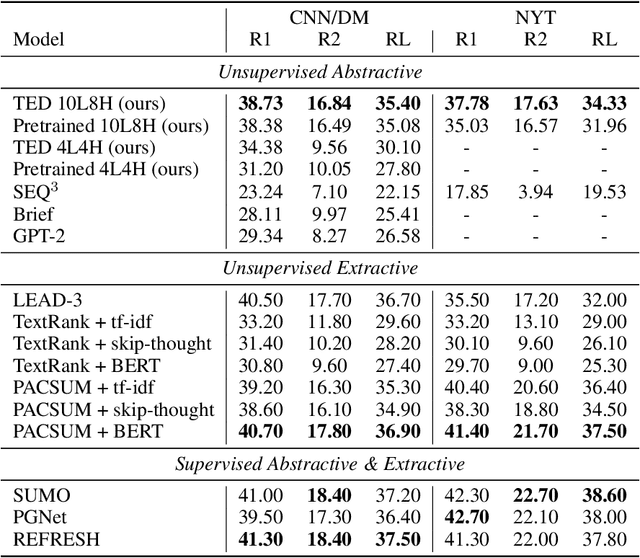
Text summarization aims to extract essential information from a piece of text and transform it into a concise version. Existing unsupervised abstractive summarization models use recurrent neural networks framework and ignore abundant unlabeled corpora resources. In order to address these issues, we propose TED, a transformer-based unsupervised summarization system with pretraining on large-scale data. We first leverage the lead bias in news articles to pretrain the model on large-scale corpora. Then, we finetune TED on target domains through theme modeling and a denoising autoencoder to enhance the quality of summaries. Notably, TED outperforms all unsupervised abstractive baselines on NYT, CNN/DM and English Gigaword datasets with various document styles. Further analysis shows that the summaries generated by TED are abstractive and containing even higher proportions of novel tokens than those from supervised models.

Embedding Imputation with Grounded Language Information

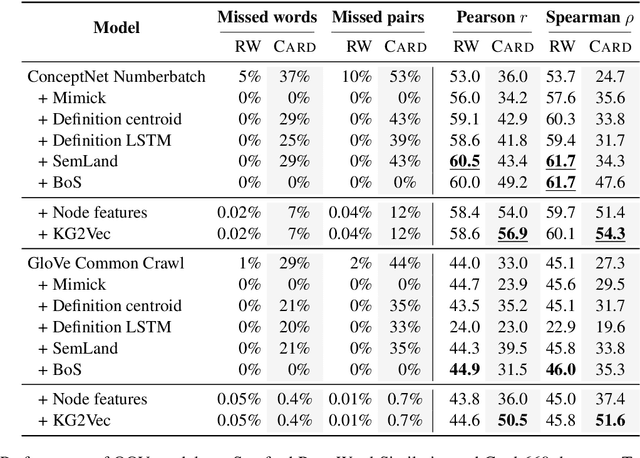
Due to the ubiquitous use of embeddings as input representations for a wide range of natural language tasks, imputation of embeddings for rare and unseen words is a critical problem in language processing. Embedding imputation involves learning representations for rare or unseen words during the training of an embedding model, often in a post-hoc manner. In this paper, we propose an approach for embedding imputation which uses grounded information in the form of a knowledge graph. This is in contrast to existing approaches which typically make use of vector space properties or subword information. We propose an online method to construct a graph from grounded information and design an algorithm to map from the resulting graphical structure to the space of the pre-trained embeddings. Finally, we evaluate our approach on a range of rare and unseen word tasks across various domains and show that our model can learn better representations. For example, on the Card-660 task our method improves Pearson's and Spearman's correlation coefficients upon the state-of-the-art by 11% and 17.8% respectively using GloVe embeddings.

Calibrating Lévy Process from Observations Based on Neural Networks and Automatic Differentiation with Convergence Proofs

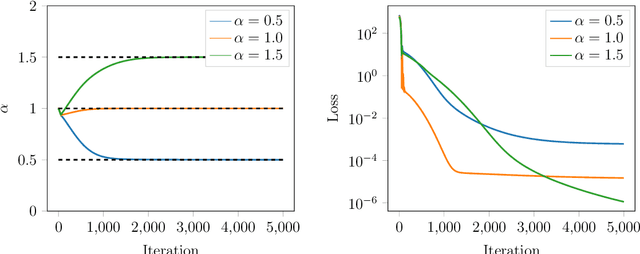
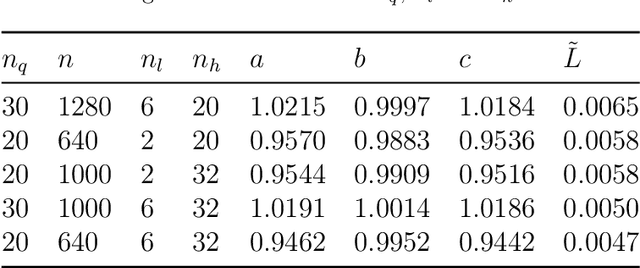
The L\'evy process has been widely applied to mathematical finance, quantum mechanics, peridynamics, and so on. However, calibrating the nonparametric multivariate distribution related to the L\'evy process from observations is a very challenging problem due to the lack of explicit distribution functions. In this paper, we propose a novel algorithm based on neural networks and automatic differentiation for solving this problem. We use neural networks to approximate the nonparametric part and discretize the characteristic exponents using accuracy numerical quadratures. Automatic differentiation is then applied to compute gradients and we minimize the mismatch between empirical and exact characteristic exponents using first-order optimization approaches. Another distinctive contribution of our work is that we made an effort to investigate the approximation ability of neural networks and the convergence behavior of algorithms. We derived the estimated number of neurons for a two-layer neural network. To achieve an accuracy of $\varepsilon$ with the input dimension $d$, it is sufficient to build $\mathcal{O}\left(\left(\frac{d}{\varepsilon} \right)^2\right)$ and $\mathcal{O}\left(\frac{d}{\varepsilon} \right)$ for the first and second layers. The numbers are polynomial in the input dimension compared to the exponential $\mathcal{O}\left(\varepsilon^{-d} \right)$ for one. We also give the convergence proof of the neural network concerning the training samples under mild assumptions and show that the RMSE decreases linearly in the number of training data in the consistency error dominancy region for the 2D problem. It is the first-ever convergence analysis for such an algorithm in literature to our best knowledge. Finally, we apply the algorithms to the stock markets and reveal some interesting patterns in the pairwise $\alpha$ index.

Block Basis Factorization for Scalable Kernel Matrix Evaluation

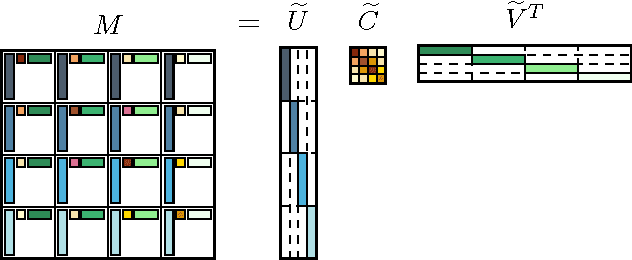
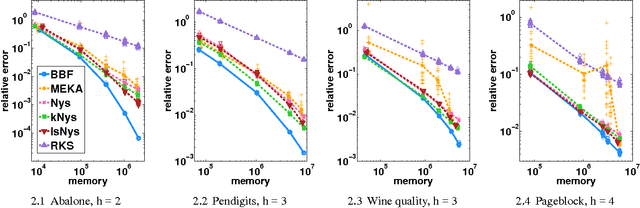
Kernel methods are widespread in machine learning; however, they are limited by the quadratic complexity of the construction, application, and storage of kernel matrices. Low-rank matrix approximation algorithms are widely used to address this problem and reduce the arithmetic and storage cost. However, we observed that for some datasets with wide intra-class variability, the optimal kernel parameter for smaller classes yields a matrix that is less well approximated by low-rank methods. In this paper, we propose an efficient structured low-rank approximation method---the Block Basis Factorization (BBF)---and its fast construction algorithm to approximate radial basis function (RBF) kernel matrices. Our approach has linear memory cost and floating point operations. BBF works for a wide range of kernel bandwidth parameters and extends the domain of applicability of low-rank approximation methods significantly. Our empirical results demonstrate the stability and superiority over the state-of-art kernel approximation algorithms.