The staircase property: How hierarchical structure can guide deep learning

This paper identifies a structural property of data distributions that enables deep neural networks to learn hierarchically. We define the "staircase" property for functions over the Boolean hypercube, which posits that high-order Fourier coefficients are reachable from lower-order Fourier coefficients along increasing chains. We prove that functions satisfying this property can be learned in polynomial time using layerwise stochastic coordinate descent on regular neural networks -- a class of network architectures and initializations that have homogeneity properties. Our analysis shows that for such staircase functions and neural networks, the gradient-based algorithm learns high-level features by greedily combining lower-level features along the depth of the network. We further back our theoretical results with experiments showing that staircase functions are also learnable by more standard ResNet architectures with stochastic gradient descent. Both the theoretical and experimental results support the fact that staircase properties have a role to play in understanding the capabilities of gradient-based learning on regular networks, in contrast to general polynomial-size networks that can emulate any SQ or PAC algorithms as recently shown.

On the Power of Differentiable Learning versus PAC and SQ Learning

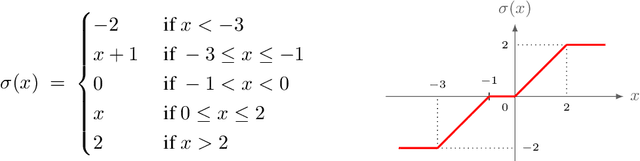
We study the power of learning via mini-batch stochastic gradient descent (SGD) on the population loss, and batch Gradient Descent (GD) on the empirical loss, of a differentiable model or neural network, and ask what learning problems can be learnt using these paradigms. We show that SGD and GD can always simulate learning with statistical queries (SQ), but their ability to go beyond that depends on the precision $\rho$ of the gradient calculations relative to the minibatch size $b$ (for SGD) and sample size $m$ (for GD). With fine enough precision relative to minibatch size, namely when $b \rho$ is small enough, SGD can go beyond SQ learning and simulate any sample-based learning algorithm and thus its learning power is equivalent to that of PAC learning; this extends prior work that achieved this result for $b=1$. Similarly, with fine enough precision relative to the sample size $m$, GD can also simulate any sample-based learning algorithm based on $m$ samples. In particular, with polynomially many bits of precision (i.e. when $\rho$ is exponentially small), SGD and GD can both simulate PAC learning regardless of the mini-batch size. On the other hand, when $b \rho^2$ is large enough, the power of SGD is equivalent to that of SQ learning.

Quantifying the Benefit of Using Differentiable Learning over Tangent Kernels

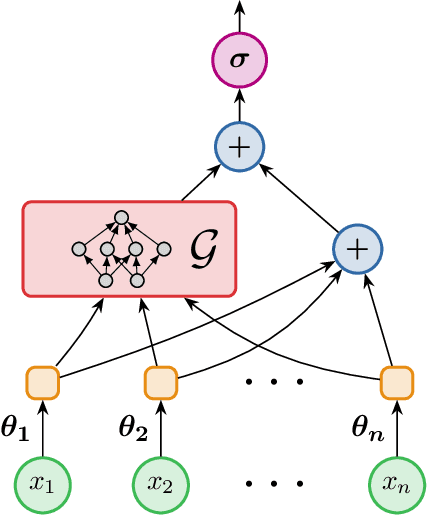
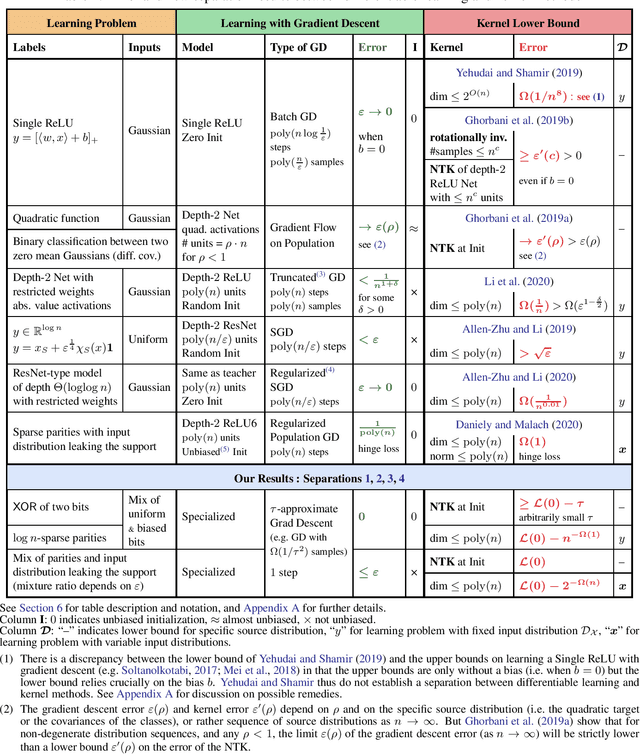
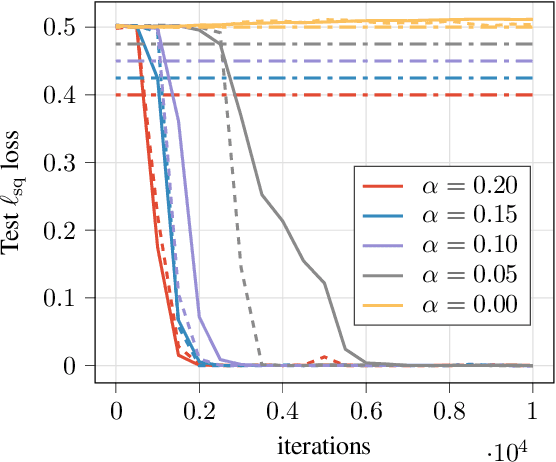
We study the relative power of learning with gradient descent on differentiable models, such as neural networks, versus using the corresponding tangent kernels. We show that under certain conditions, gradient descent achieves small error only if a related tangent kernel method achieves a non-trivial advantage over random guessing (a.k.a. weak learning), though this advantage might be very small even when gradient descent can achieve arbitrarily high accuracy. Complementing this, we show that without these conditions, gradient descent can in fact learn with small error even when no kernel method, in particular using the tangent kernel, can achieve a non-trivial advantage over random guessing.

Proof of the Contiguity Conjecture and Lognormal Limit for the Symmetric Perceptron

We consider the symmetric binary perceptron model, a simple model of neural networks that has gathered significant attention in the statistical physics, information theory and probability theory communities, with recent connections made to the performance of learning algorithms in Baldassi et al. '15. We establish that the partition function of this model, normalized by its expected value, converges to a lognormal distribution. As a consequence, this allows us to establish several conjectures for this model: (i) it proves the contiguity conjecture of Aubin et al. '19 between the planted and unplanted models in the satisfiable regime; (ii) it establishes the sharp threshold conjecture; (iii) it proves the frozen 1-RSB conjecture in the symmetric case, conjectured first by Krauth-M\'ezard '89 in the asymmetric case. In a recent concurrent work of Perkins-Xu [PX21], the last two conjectures were also established by proving that the partition function concentrates on an exponential scale. This left open the contiguity conjecture and the lognormal limit characterization, which are established here. In particular, our proof technique relies on a dense counter-part of the small graph conditioning method, which was developed for sparse models in the celebrated work of Robinson and Wormald.

Maximum Multiscale Entropy and Neural Network Regularization

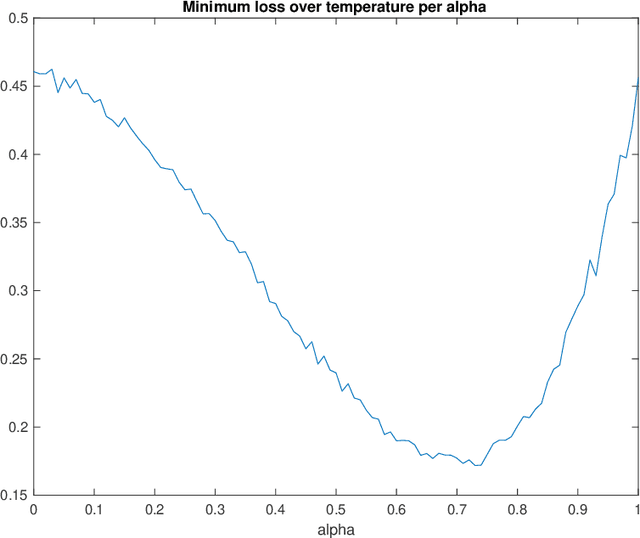
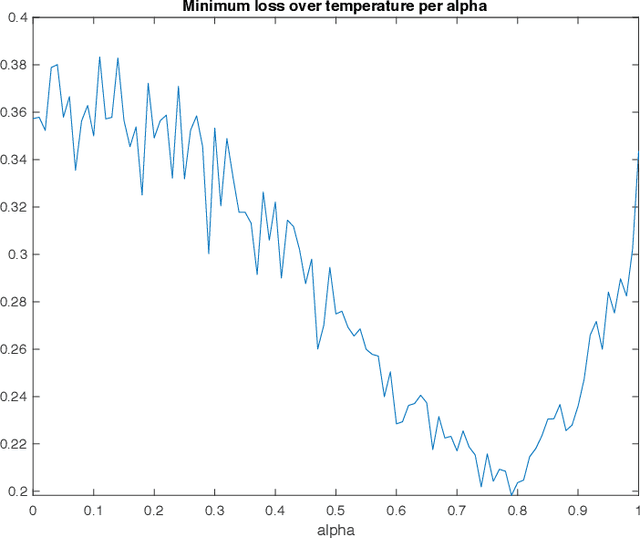
A well-known result across information theory, machine learning, and statistical physics shows that the maximum entropy distribution under a mean constraint has an exponential form called the Gibbs-Boltzmann distribution. This is used for instance in density estimation or to achieve excess risk bounds derived from single-scale entropy regularizers (Xu-Raginsky '17). This paper investigates a generalization of these results to a multiscale setting. We present different ways of generalizing the maximum entropy result by incorporating the notion of scale. For different entropies and arbitrary scale transformations, it is shown that the distribution maximizing a multiscale entropy is characterized by a procedure which has an analogy to the renormalization group procedure in statistical physics. For the case of decimation transformation, it is further shown that this distribution is Gaussian whenever the optimal single-scale distribution is Gaussian. This is then applied to neural networks, and it is shown that in a teacher-student scenario, the multiscale Gibbs posterior can achieve a smaller excess risk than the single-scale Gibbs posterior.

An $\ell_p$ theory of PCA and spectral clustering

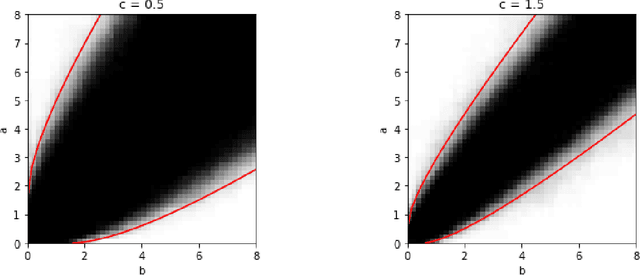
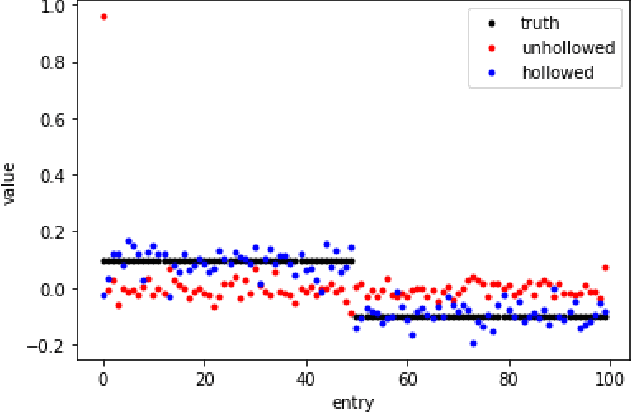
Principal Component Analysis (PCA) is a powerful tool in statistics and machine learning. While existing study of PCA focuses on the recovery of principal components and their associated eigenvalues, there are few precise characterizations of individual principal component scores that yield low-dimensional embedding of samples. That hinders the analysis of various spectral methods. In this paper, we first develop an $\ell_p$ perturbation theory for a hollowed version of PCA in Hilbert spaces which provably improves upon the vanilla PCA in the presence of heteroscedastic noises. Through a novel $\ell_p$ analysis of eigenvectors, we investigate entrywise behaviors of principal component score vectors and show that they can be approximated by linear functionals of the Gram matrix in $\ell_p$ norm, which includes $\ell_2$ and $\ell_\infty$ as special examples. For sub-Gaussian mixture models, the choice of $p$ giving optimal bounds depends on the signal-to-noise ratio, which further yields optimality guarantees for spectral clustering. For contextual community detection, the $\ell_p$ theory leads to a simple spectral algorithm that achieves the information threshold for exact recovery. These also provide optimal recovery results for Gaussian mixture and stochastic block models as special cases.

Learning Sparse Graphons and the Generalized Kesten-Stigum Threshold

The problem of learning graphons has attracted considerable attention across several scientific communities, with significant progress over the recent years in sparser regimes. Yet, the current techniques still require diverging degrees in order to succeed with efficient algorithms in the challenging cases where the local structure of the graph is homogeneous. This paper provides an efficient algorithm to learn graphons in the constant expected degree regime. The algorithm is shown to succeed in estimating the rank-$k$ projection of a graphon in the $L_2$ metric if the top $k$ eigenvalues of the graphon satisfy a generalized Kesten-Stigum condition.

Poly-time universality and limitations of deep learning

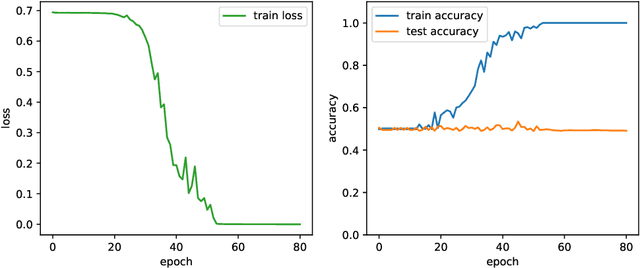
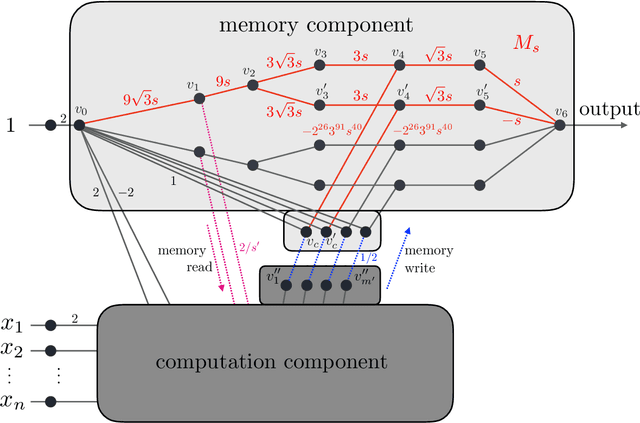
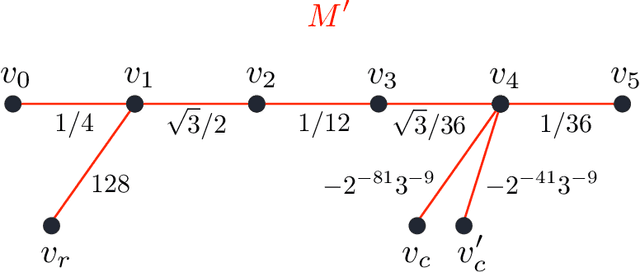
The goal of this paper is to characterize function distributions that deep learning can or cannot learn in poly-time. A universality result is proved for SGD-based deep learning and a non-universality result is proved for GD-based deep learning; this also gives a separation between SGD-based deep learning and statistical query algorithms: (1) {\it Deep learning with SGD is efficiently universal.} Any function distribution that can be learned from samples in poly-time can also be learned by a poly-size neural net trained with SGD on a poly-time initialization with poly-steps, poly-rate and possibly poly-noise. Therefore deep learning provides a universal learning paradigm: it was known that the approximation and estimation errors could be controlled with poly-size neural nets, using ERM that is NP-hard; this new result shows that the optimization error can also be controlled with SGD in poly-time. The picture changes for GD with large enough batches: (2) {\it Result (1) does not hold for GD:} Neural nets of poly-size trained with GD (full gradients or large enough batches) on any initialization with poly-steps, poly-range and at least poly-noise cannot learn any function distribution that has super-polynomial {\it cross-predictability,} where the cross-predictability gives a measure of ``average'' function correlation -- relations and distinctions to the statistical dimension are discussed. In particular, GD with these constraints can learn efficiently monomials of degree $k$ if and only if $k$ is constant. Thus (1) and (2) point to an interesting contrast: SGD is universal even with some poly-noise while full GD or SQ algorithms are not (e.g., parities).

Chaining Meets Chain Rule: Multilevel Entropic Regularization and Training of Neural Nets

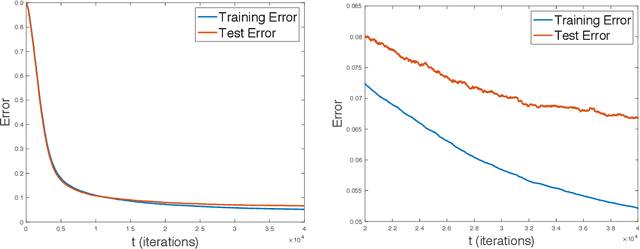
We derive generalization and excess risk bounds for neural nets using a family of complexity measures based on a multilevel relative entropy. The bounds are obtained by introducing the notion of generated hierarchical coverings of neural nets and by using the technique of chaining mutual information introduced in Asadi et al. NeurIPS'18. The resulting bounds are algorithm-dependent and exploit the multilevel structure of neural nets. This, in turn, leads to an empirical risk minimization problem with a multilevel entropic regularization. The minimization problem is resolved by introducing a multi-scale generalization of the celebrated Gibbs posterior distribution, proving that the derived distribution achieves the unique minimum. This leads to a new training procedure for neural nets with performance guarantees, which exploits the chain rule of relative entropy rather than the chain rule of derivatives (as in backpropagation). To obtain an efficient implementation of the latter, we further develop a multilevel Metropolis algorithm simulating the multi-scale Gibbs distribution, with an experiment for a two-layer neural net on the MNIST data set.

Provable limitations of deep learning

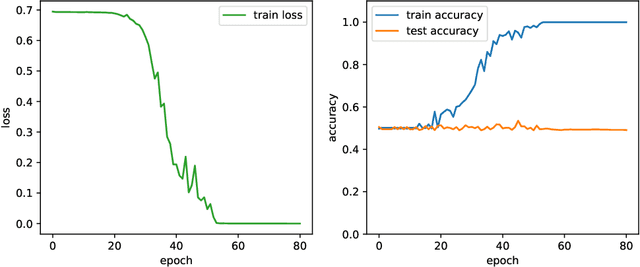
As the success of deep learning reaches more grounds, one would like to also envision the potential limits of deep learning. This paper gives a first set of results proving that deep learning algorithms fail at learning certain efficiently learnable functions. Parity functions form the running example of our results and the paper puts forward a notion of low cross-predictability that defines a more general class of functions for which such failures tend to generalize (with examples in community detection and arithmetic learning). Recall that it is known that the class of neural networks (NNs) with polynomial network size can express any function that can be implemented in polynomial time, and that their sample complexity scales polynomially with the network size. The challenge is with the optimization error (the ERM is NP-hard), and the success behind deep learning is to train deep NNs with descent algorithms. The failures shown in this paper apply to training poly-size NNs on function distributions of low cross-predictability with a descent algorithm that is either run with limited memory per sample or that is initialized and run with enough randomness (exponentially small for GD). We further claim that such types of constraints are necessary to obtain failures, in that exact SGD with careful non-random initialization can learn parities. The cross-predictability notion has some similarity with the statistical dimension used in statistical query (SQ) algorithms, however the two definitions are different for reasons explained in the paper. The proof techniques are based on exhibiting algorithmic constraints that imply a statistical indistinguishability between the algorithm's output on the test model v.s.\ a null model, using information measures to bound the total variation distance.