Leveraging PAC-Bayes Theory and Gibbs Distributions for Generalization Bounds with Complexity Measures

In statistical learning theory, a generalization bound usually involves a complexity measure imposed by the considered theoretical framework. This limits the scope of such bounds, as other forms of capacity measures or regularizations are used in algorithms. In this paper, we leverage the framework of disintegrated PAC-Bayes bounds to derive a general generalization bound instantiable with arbitrary complexity measures. One trick to prove such a result involves considering a commonly used family of distributions: the Gibbs distributions. Our bound stands in probability jointly over the hypothesis and the learning sample, which allows the complexity to be adapted to the generalization gap as it can be customized to fit both the hypothesis class and the task.

Learning Stochastic Majority Votes by Minimizing a PAC-Bayes Generalization Bound

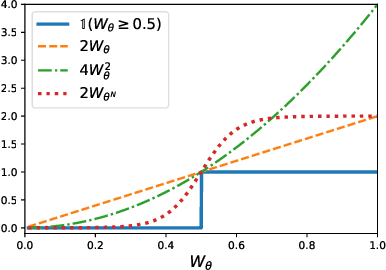
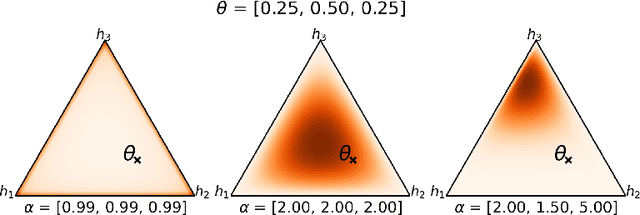
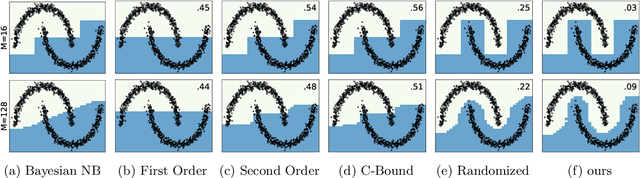
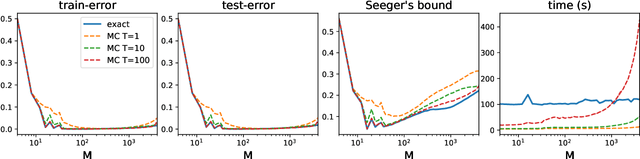
We investigate a stochastic counterpart of majority votes over finite ensembles of classifiers, and study its generalization properties. While our approach holds for arbitrary distributions, we instantiate it with Dirichlet distributions: this allows for a closed-form and differentiable expression for the expected risk, which then turns the generalization bound into a tractable training objective. The resulting stochastic majority vote learning algorithm achieves state-of-the-art accuracy and benefits from (non-vacuous) tight generalization bounds, in a series of numerical experiments when compared to competing algorithms which also minimize PAC-Bayes objectives -- both with uninformed (data-independent) and informed (data-dependent) priors.

Self-Bounding Majority Vote Learning Algorithms by the Direct Minimization of a Tight PAC-Bayesian C-Bound

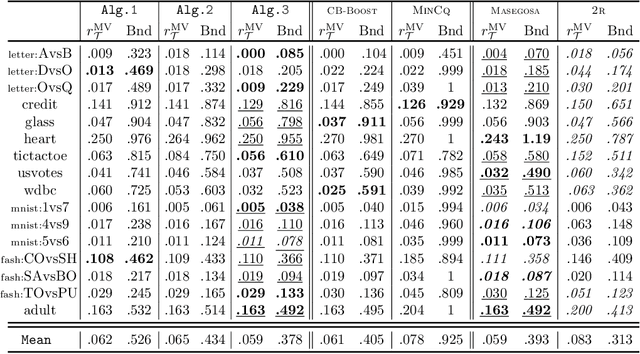
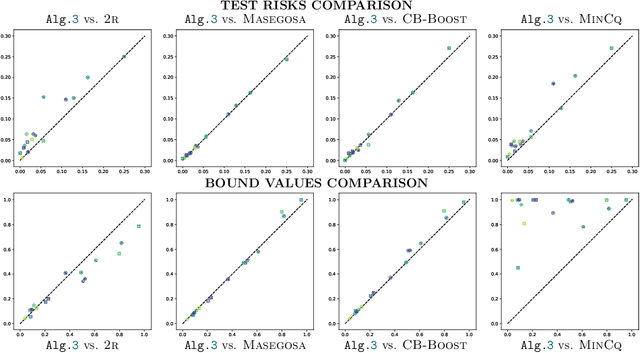
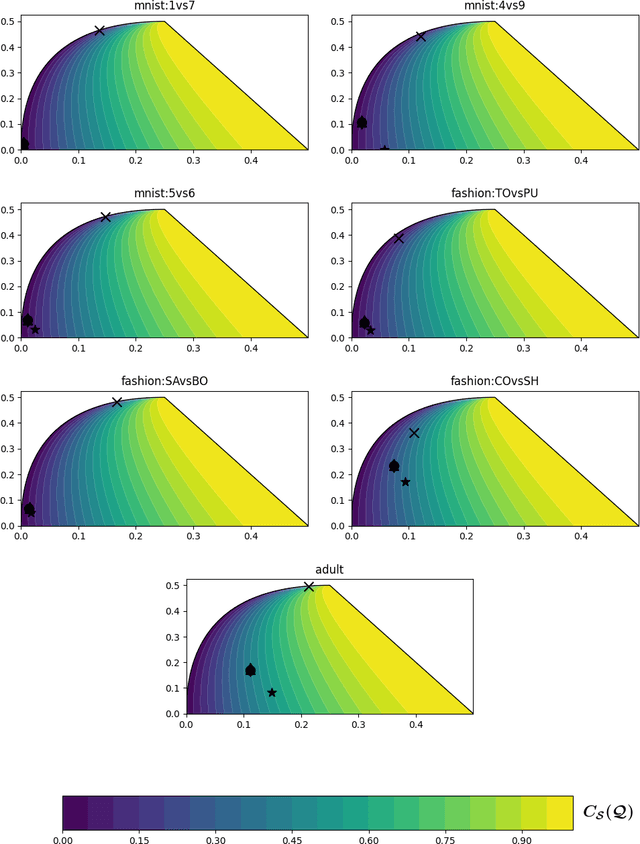
In the PAC-Bayesian literature, the C-Bound refers to an insightful relation between the risk of a majority vote classifier (under the zero-one loss) and the first two moments of its margin (i.e., the expected margin and the voters' diversity). Until now, learning algorithms developed in this framework minimize the empirical version of the C-Bound, instead of explicit PAC-Bayesian generalization bounds. In this paper, by directly optimizing PAC-Bayesian guarantees on the C-Bound, we derive self-bounding majority vote learning algorithms. Moreover, our algorithms based on gradient descent are scalable and lead to accurate predictors paired with non-vacuous guarantees.

A PAC-Bayes Analysis of Adversarial Robustness

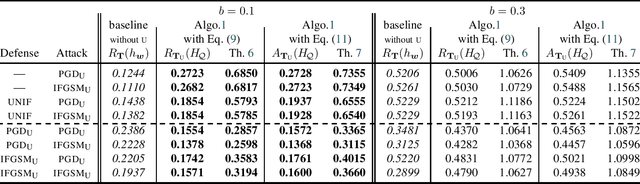
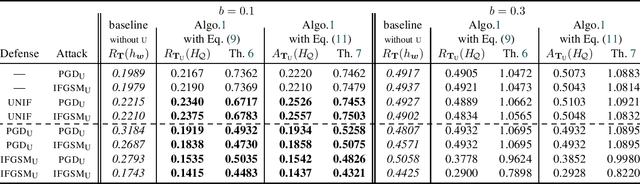
We propose the first general PAC-Bayesian generalization bounds for adversarial robustness, that estimate, at test time, how much a model will be invariant to imperceptible perturbations in the input. Instead of deriving a worst-case analysis of the risk of a hypothesis over all the possible perturbations, we leverage the PAC-Bayesian framework to bound the averaged risk on the perturbations for majority votes (over the whole class of hypotheses). Our theoretically founded analysis has the advantage to provide general bounds (i) independent from the type of perturbations (i.e., the adversarial attacks), (ii) that are tight thanks to the PAC-Bayesian framework, (iii) that can be directly minimized during the learning phase to obtain a robust model on different attacks at test time.

A General Framework for the Derandomization of PAC-Bayesian Bounds

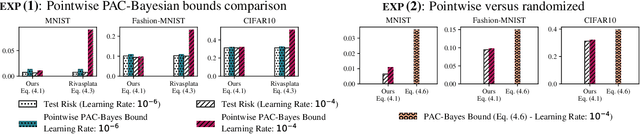
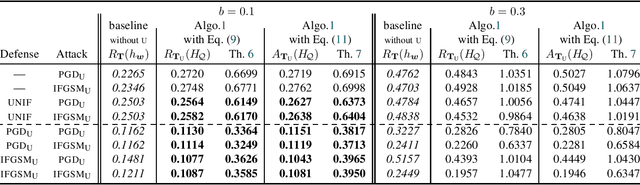
PAC-Bayesian bounds are known to be tight and informative when studying the generalization ability of randomized classifiers. However, when applied to some family of deterministic models such as neural networks, they require a loose and costly derandomization step. As an alternative to this step, we introduce three new PAC-Bayesian generalization bounds that have the originality to be pointwise, meaning that they provide guarantees over one single hypothesis instead of the usual averaged analysis. Our bounds are rather general, potentially parameterizable, and provide novel insights for various machine learning settings that rely on randomized algorithms. We illustrate the interest of our theoretical result for the analysis of neural network training.

A survey on domain adaptation theory

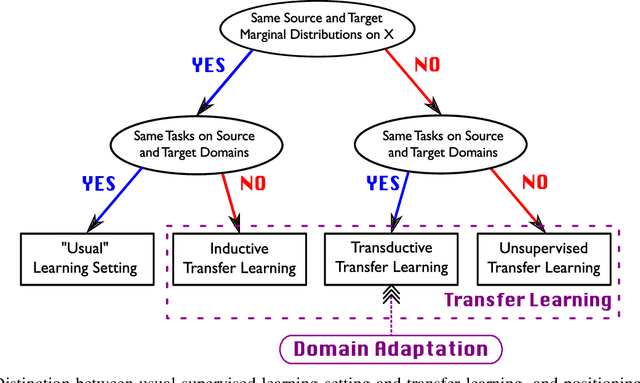
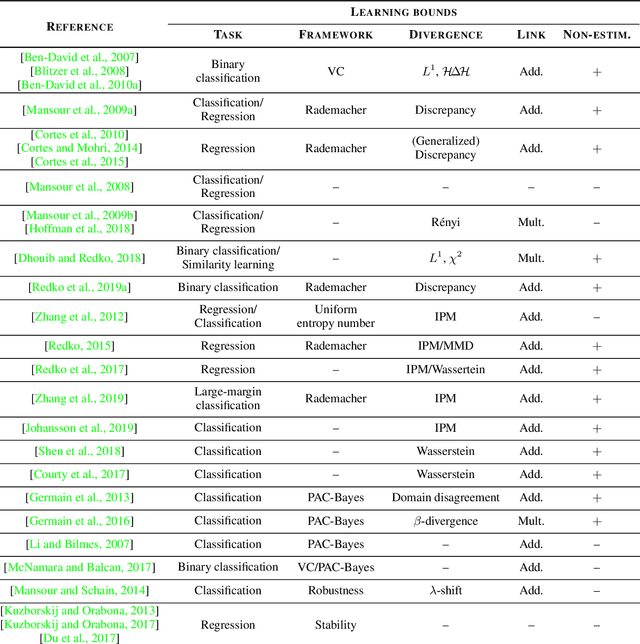
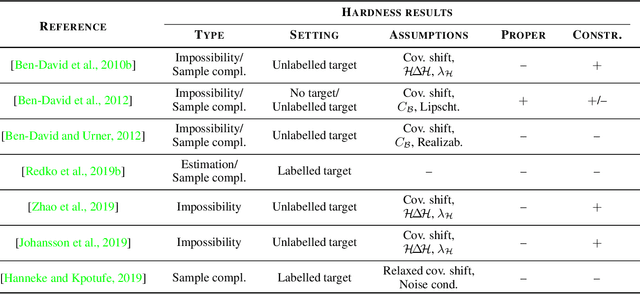
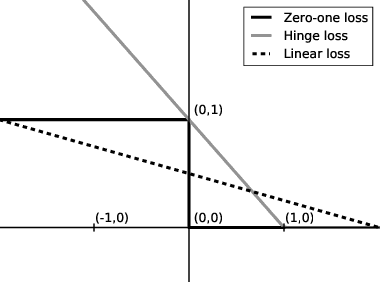
All famous machine learning algorithms that correspond to both supervised and semi-supervised learning work well only under a common assumption: training and test data follow the same distribution. When the distribution changes, most statistical models must be reconstructed from new collected data that, for some applications, may be costly or impossible to get. Therefore, it became necessary to develop approaches that reduce the need and the effort of obtaining new labeled samples by exploiting data available in related areas and using it further in similar fields. This has given rise to a new machine learning framework called transfer learning: a learning setting inspired by the capability of a human being to extrapolate knowledge across tasks to learn more efficiently. Despite a large amount of different transfer learning scenarios, the main objective of this survey is to provide an overview of the state-of-the-art theoretical results in a specific and arguably the most popular sub-field of transfer learning called domain adaptation. In this sub-field, the data distribution is assumed to change across the training and the test data while the learning task remains the same. We provide a first up-to-date description of existing results related to domain adaptation problem that cover learning bounds based on different statistical learning frameworks.

Metric Learning from Imbalanced Data

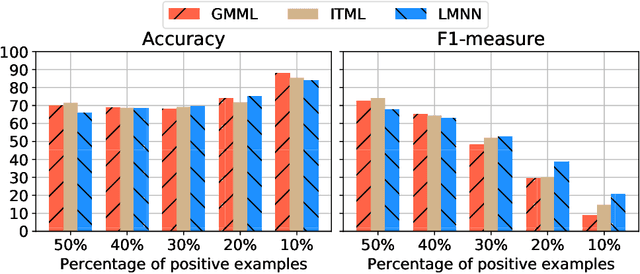
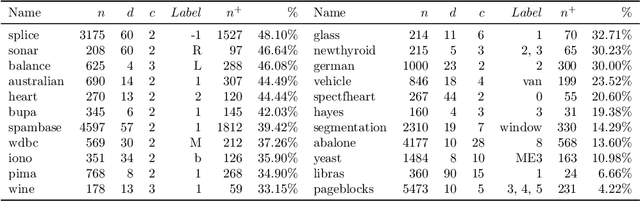
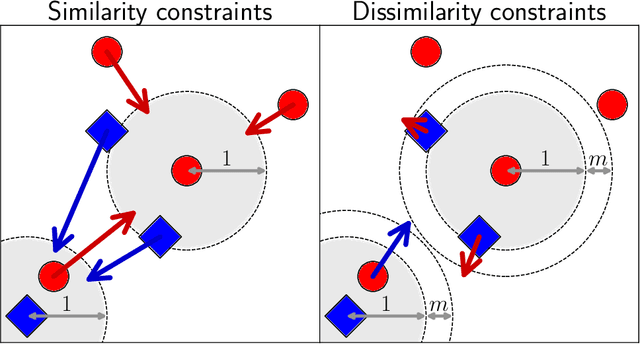
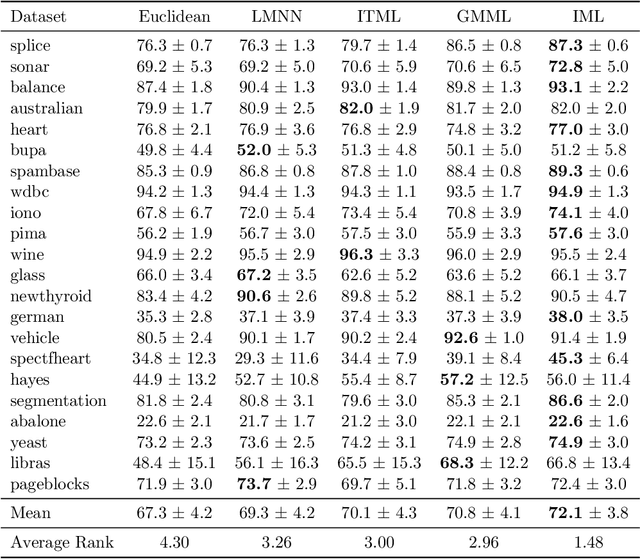
A key element of any machine learning algorithm is the use of a function that measures the dis/similarity between data points. Given a task, such a function can be optimized with a metric learning algorithm. Although this research field has received a lot of attention during the past decade, very few approaches have focused on learning a metric in an imbalanced scenario where the number of positive examples is much smaller than the negatives. Here, we address this challenging task by designing a new Mahalanobis metric learning algorithm (IML) which deals with class imbalance. The empirical study performed shows the efficiency of IML.

Learning Landmark-Based Ensembles with Random Fourier Features and Gradient Boosting

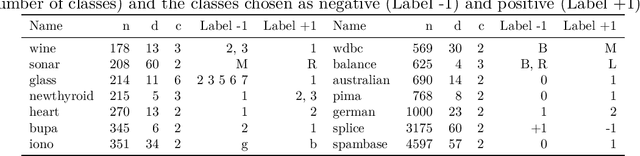
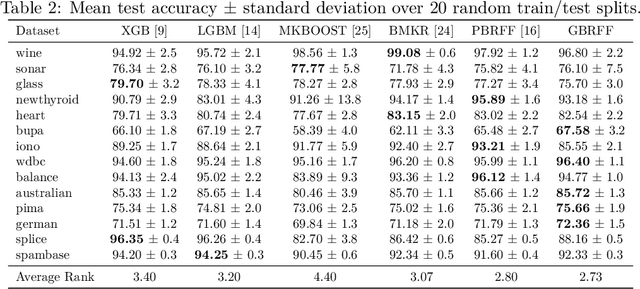
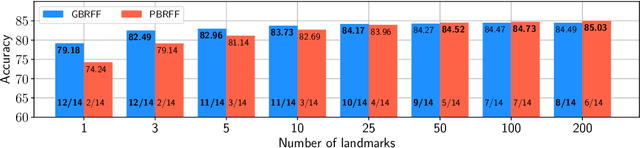
We propose a Gradient Boosting algorithm for learning an ensemble of kernel functions adapted to the task at hand. Unlike state-of-the-art Multiple Kernel Learning techniques that make use of a pre-computed dictionary of kernel functions to select from, at each iteration we fit a kernel by approximating it as a weighted sum of Random Fourier Features (RFF) and by optimizing their barycenter. This allows us to obtain a more versatile method, easier to setup and likely to have better performance. Our study builds on a recent result showing one can learn a kernel from RFF by computing the minimum of a PAC-Bayesian bound on the kernel alignment generalization loss, which is obtained efficiently from a closed-form solution. We conduct an experimental analysis to highlight the advantages of our method w.r.t. both Boosting-based and kernel-learning state-of-the-art methods.

Pseudo-Bayesian Learning with Kernel Fourier Transform as Prior

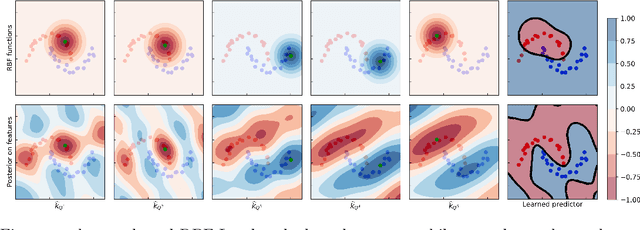
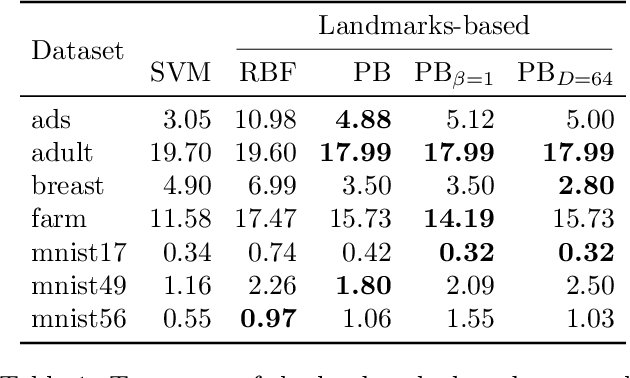
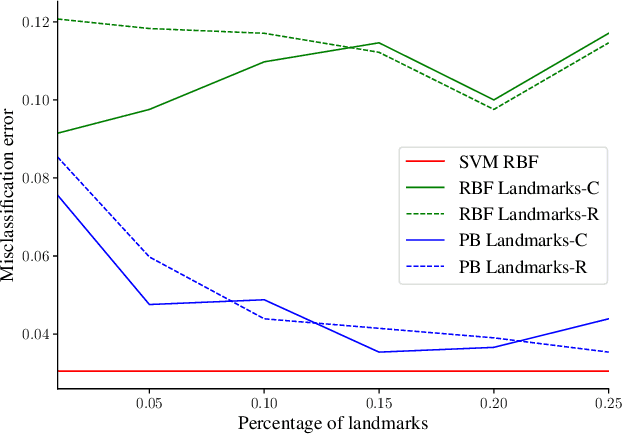
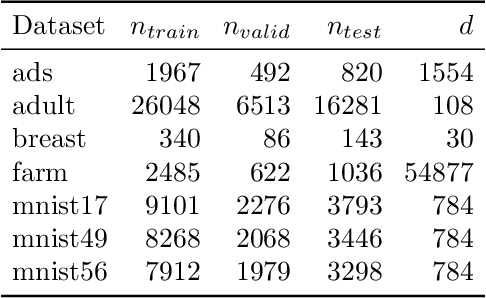
We revisit Rahimi and Recht (2007)'s kernel random Fourier features (RFF) method through the lens of the PAC-Bayesian theory. While the primary goal of RFF is to approximate a kernel, we look at the Fourier transform as a prior distribution over trigonometric hypotheses. It naturally suggests learning a posterior on these hypotheses. We derive generalization bounds that are optimized by learning a pseudo-posterior obtained from a closed-form expression. Based on this study, we consider two learning strategies: The first one finds a compact landmarks-based representation of the data where each landmark is given by a distribution-tailored similarity measure, while the second one provides a PAC-Bayesian justification to the kernel alignment method of Sinha and Duchi (2016).

Multiview Boosting by Controlling the Diversity and the Accuracy of View-specific Voters

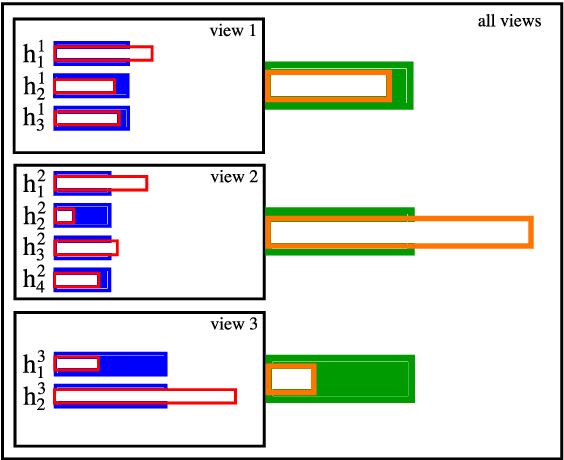
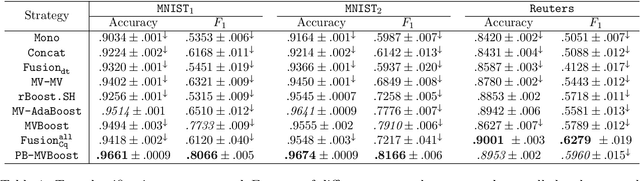
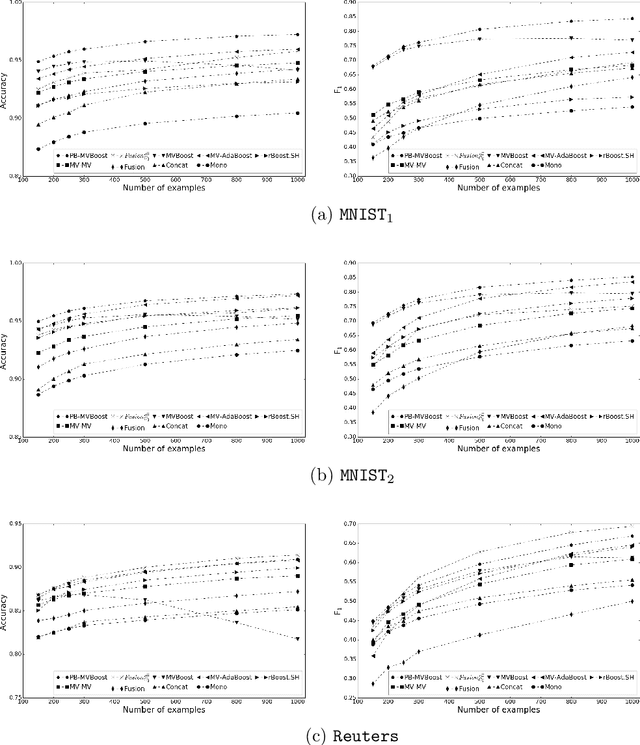
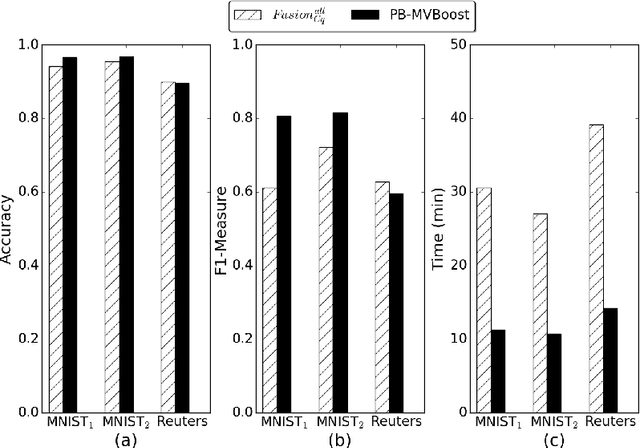
In this paper we propose a boosting based multiview learning algorithm, referred to as PB-MVBoost, which iteratively learns i) weights over view-specific voters capturing view-specific information; and ii) weights over views by optimizing a PAC-Bayes multiview C-Bound that takes into account the accuracy of view-specific classifiers and the diversity between the views. We derive a generalization bound for this strategy following the PAC-Bayes theory which is a suitable tool to deal with models expressed as weighted combination over a set of voters. Different experiments on three publicly available datasets show the efficiency of the proposed approach with respect to state-of-art models.