Emile Mathieu
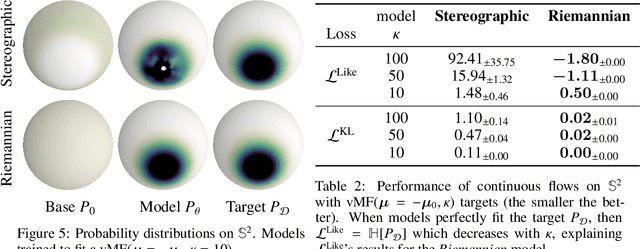
Riemannian Diffusion Schrödinger Bridge
Jul 07, 2022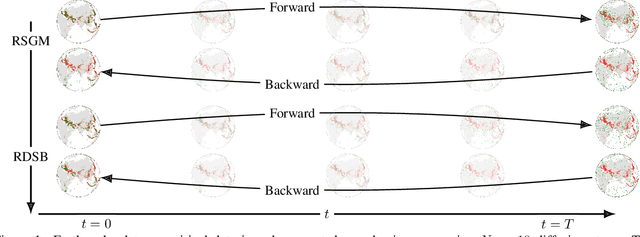
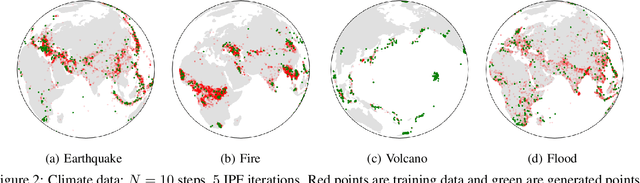

Abstract:Score-based generative models exhibit state of the art performance on density estimation and generative modeling tasks. These models typically assume that the data geometry is flat, yet recent extensions have been developed to synthesize data living on Riemannian manifolds. Existing methods to accelerate sampling of diffusion models are typically not applicable in the Riemannian setting and Riemannian score-based methods have not yet been adapted to the important task of interpolation of datasets. To overcome these issues, we introduce \emph{Riemannian Diffusion Schr\"odinger Bridge}. Our proposed method generalizes Diffusion Schr\"odinger Bridge introduced in \cite{debortoli2021neurips} to the non-Euclidean setting and extends Riemannian score-based models beyond the first time reversal. We validate our proposed method on synthetic data and real Earth and climate data.
Learning Instance-Specific Data Augmentations
May 31, 2022
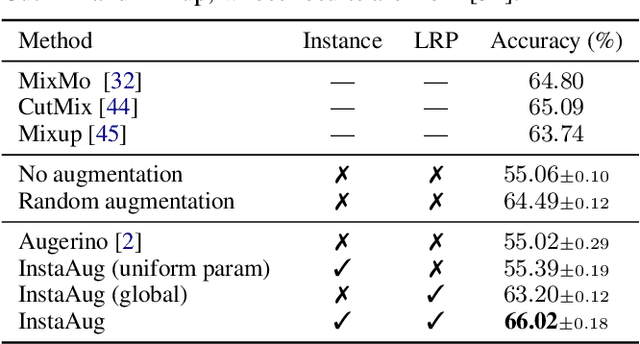
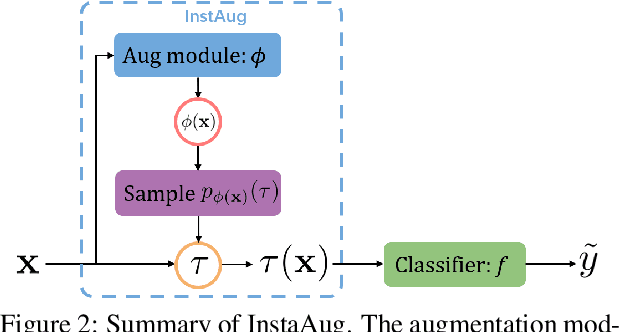
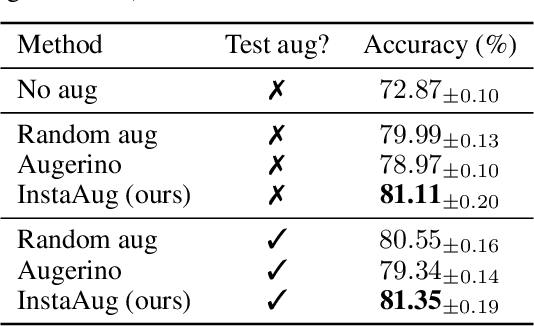
Abstract:Existing data augmentation methods typically assume independence between transformations and inputs: they use the same transformation distribution for all input instances. We explain why this can be problematic and propose InstaAug, a method for automatically learning input-specific augmentations from data. This is achieved by introducing an augmentation module that maps an input to a distribution over transformations. This is simultaneously trained alongside the base model in a fully end-to-end manner using only the training data. We empirically demonstrate that InstaAug learns meaningful augmentations for a wide range of transformation classes, which in turn provides better performance on supervised and self-supervised tasks compared with augmentations that assume input--transformation independence.
Riemannian Score-Based Generative Modeling
Feb 06, 2022
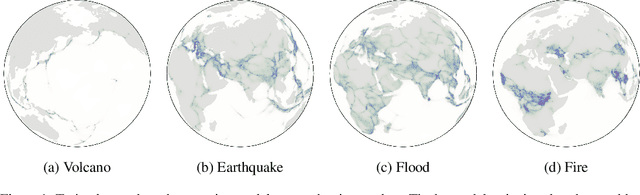

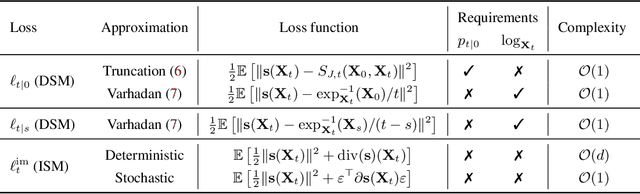
Abstract:Score-based generative models (SGMs) are a novel class of generative models demonstrating remarkable empirical performance. One uses a diffusion to add progressively Gaussian noise to the data, while the generative model is a "denoising" process obtained by approximating the time-reversal of this "noising" diffusion. However, current SGMs make the underlying assumption that the data is supported on a Euclidean manifold with flat geometry. This prevents the use of these models for applications in robotics, geoscience or protein modeling which rely on distributions defined on Riemannian manifolds. To overcome this issue, we introduce Riemannian Score-based Generative Models (RSGMs) which extend current SGMs to the setting of compact Riemannian manifolds. We illustrate our approach with earth and climate science data and show how RSGMs can be accelerated by solving a Schr\"odinger bridge problem on manifolds.
InteL-VAEs: Adding Inductive Biases to Variational Auto-Encoders via Intermediary Latents
Jun 25, 2021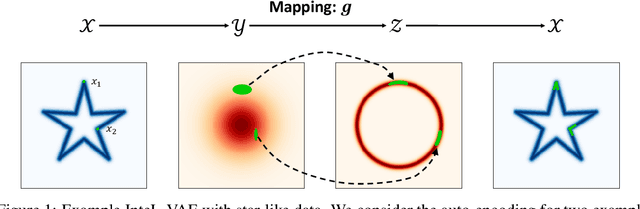


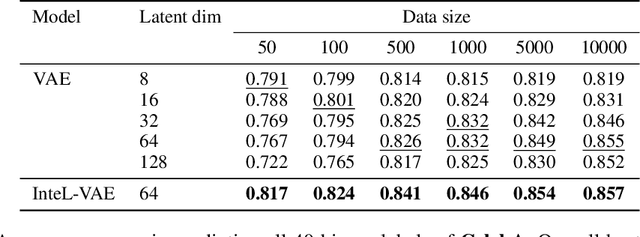
Abstract:We introduce a simple and effective method for learning VAEs with controllable inductive biases by using an intermediary set of latent variables. This allows us to overcome the limitations of the standard Gaussian prior assumption. In particular, it allows us to impose desired properties like sparsity or clustering on learned representations, and incorporate prior information into the learned model. Our approach, which we refer to as the Intermediary Latent Space VAE (InteL-VAE), is based around controlling the stochasticity of the encoding process with the intermediary latent variables, before deterministically mapping them forward to our target latent representation, from which reconstruction is performed. This allows us to maintain all the advantages of the traditional VAE framework, while incorporating desired prior information, inductive biases, and even topological information through the latent mapping. We show that this, in turn, allows InteL-VAEs to learn both better generative models and representations.
On Contrastive Representations of Stochastic Processes
Jun 18, 2021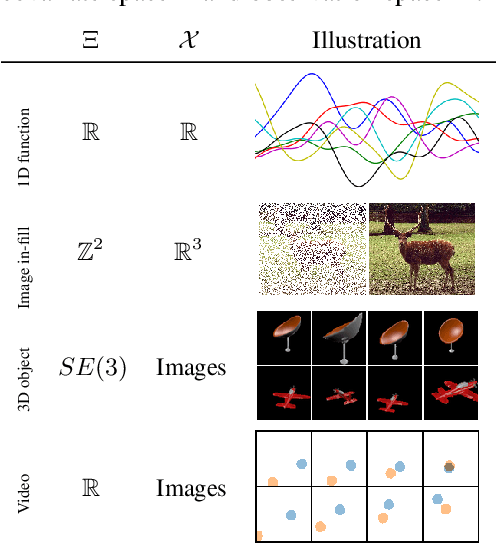
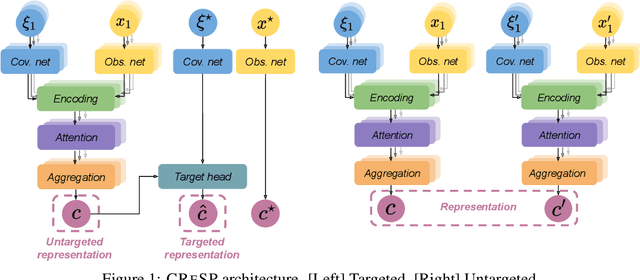

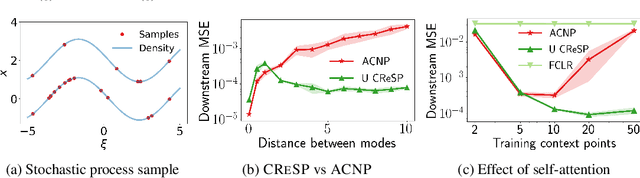
Abstract:Learning representations of stochastic processes is an emerging problem in machine learning with applications from meta-learning to physical object models to time series. Typical methods rely on exact reconstruction of observations, but this approach breaks down as observations become high-dimensional or noise distributions become complex. To address this, we propose a unifying framework for learning contrastive representations of stochastic processes (CRESP) that does away with exact reconstruction. We dissect potential use cases for stochastic process representations, and propose methods that accommodate each. Empirically, we show that our methods are effective for learning representations of periodic functions, 3D objects and dynamical processes. Our methods tolerate noisy high-dimensional observations better than traditional approaches, and the learned representations transfer to a range of downstream tasks.
Riemannian Continuous Normalizing Flows
Jun 18, 2020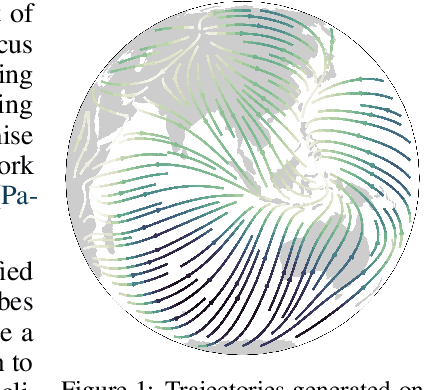

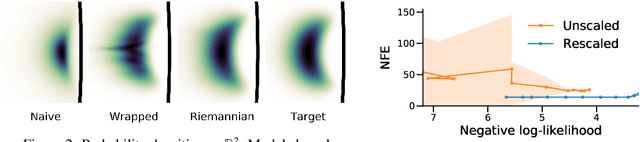
Abstract:Normalizing flows have shown great promise for modelling flexible probability distributions in a computationally tractable way. However, whilst data is often naturally described on Riemannian manifolds such as spheres, torii, and hyperbolic spaces, most normalizing flows implicitly assume a flat geometry, making them either misspecified or ill-suited in these situations. To overcome this problem, we introduce Riemannian continuous normalizing flows, a model which admits the parametrization of flexible probability measures on smooth manifolds by defining flows as the solution to ordinary differential equations. We show that this approach can lead to substantial improvements on both synthetic and real-world data when compared to standard flows or previously introduced projected flows.
Hierarchical Representations with Poincaré Variational Auto-Encoders
Jan 17, 2019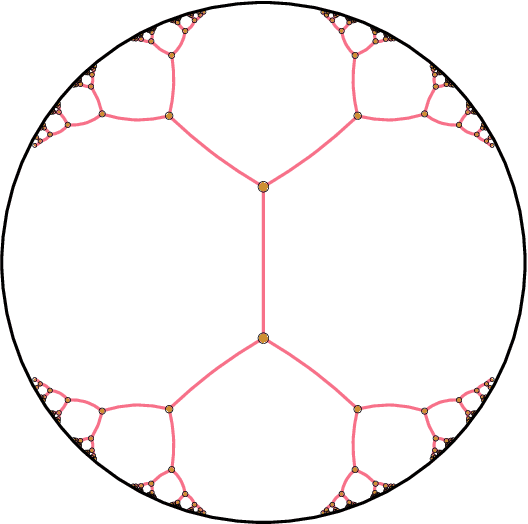

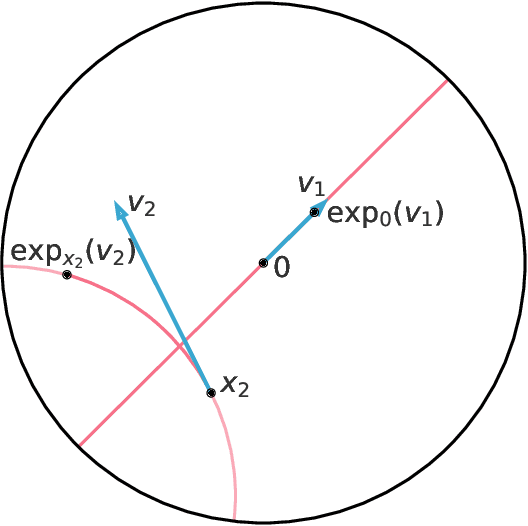
Abstract:The Variational Auto-Encoder (VAE) model has become widely popular as a way to learn at once a generative model and embeddings for observations living in a high-dimensional space. In the real world, many such observations may be assumed to be hierarchically structured, such as living organisms data which are related through the evolutionary tree. Also, it has been theoretically and empirically shown that data with hierarchical structure can efficiently be embedded in hyperbolic spaces. We therefore endow the VAE with a hyperbolic geometry and empirically show that it can better generalise to unseen data than its Euclidean counterpart, and can qualitatively recover the hierarchical structure.
Disentangling Disentanglement
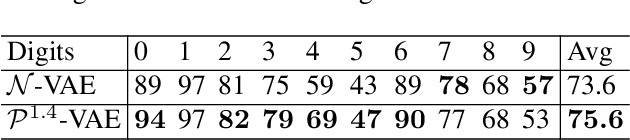
Dec 06, 2018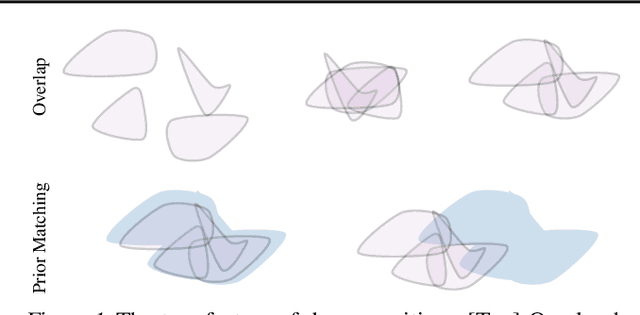
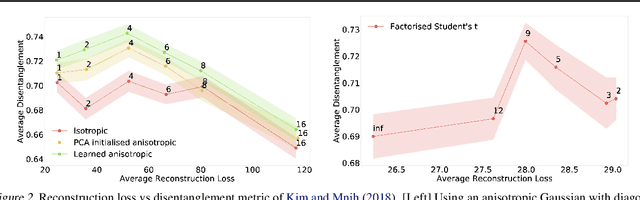
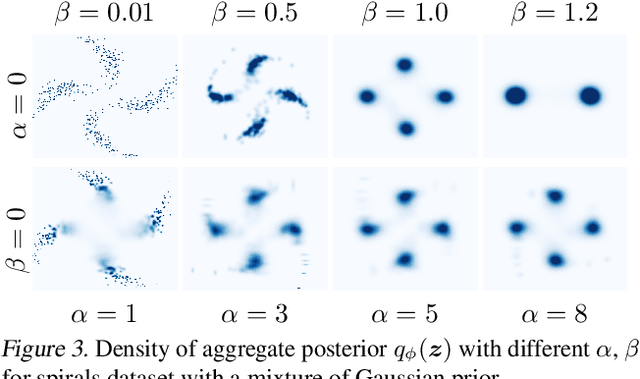
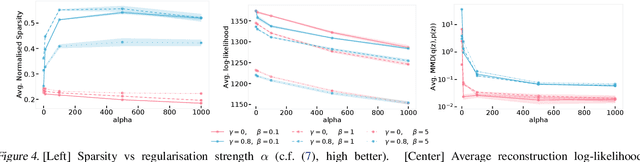
Abstract:We develop a generalised notion of disentanglement in Variational Auto-Encoders (VAEs) by casting it as a \emph{decomposition} of the latent representation, characterised by i) enforcing an appropriate level of overlap in the latent encodings of the data, and ii) regularisation of the average encoding to a desired structure, represented through the prior. We motivate this by showing that a) the $\beta$-VAE disentangles purely through regularisation of the overlap in latent encodings, and through its average (Gaussian) encoder variance, and b) disentanglement, as independence between latents, can be cast as a regularisation of the aggregate posterior to a prior with specific characteristics. We validate this characterisation by showing that simple manipulations of these factors, such as using rotationally variant priors, can help improve disentanglement, and discuss how this characterisation provides a more general framework to incorporate notions of decomposition beyond just independence between the latents.
Sampling and Inference for Beta Neutral-to-the-Left Models of Sparse Networks
Jul 09, 2018
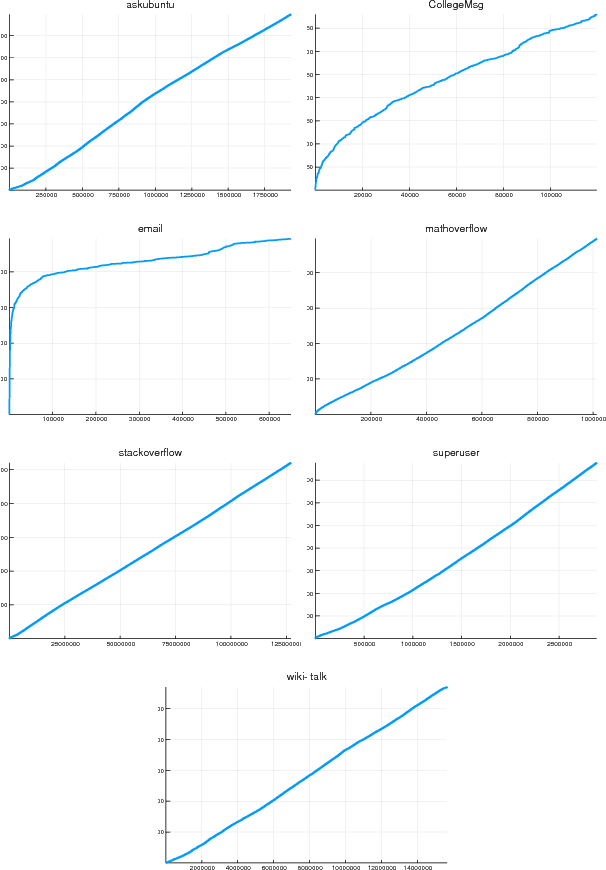


Abstract:Empirical evidence suggests that heavy-tailed degree distributions occurring in many real networks are well-approximated by power laws with exponents $\eta$ that may take values either less than and greater than two. Models based on various forms of exchangeability are able to capture power laws with $\eta < 2$, and admit tractable inference algorithms; we draw on previous results to show that $\eta > 2$ cannot be generated by the forms of exchangeability used in existing random graph models. Preferential attachment models generate power law exponents greater than two, but have been of limited use as statistical models due to the inherent difficulty of performing inference in non-exchangeable models. Motivated by this gap, we design and implement inference algorithms for a recently proposed class of models that generates $\eta$ of all possible values. We show that although they are not exchangeable, these models have probabilistic structure amenable to inference. Our methods make a large class of previously intractable models useful for statistical inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge