Efficient Learning of Interpretable Classification Rules

Machine learning has become omnipresent with applications in various safety-critical domains such as medical, law, and transportation. In these domains, high-stake decisions provided by machine learning necessitate researchers to design interpretable models, where the prediction is understandable to a human. In interpretable machine learning, rule-based classifiers are particularly effective in representing the decision boundary through a set of rules comprising input features. The interpretability of rule-based classifiers is in general related to the size of the rules, where smaller rules are considered more interpretable. To learn such a classifier, the brute-force direct approach is to consider an optimization problem that tries to learn the smallest classification rule that has close to maximum accuracy. This optimization problem is computationally intractable due to its combinatorial nature and thus, the problem is not scalable in large datasets. To this end, in this paper we study the triangular relationship among the accuracy, interpretability, and scalability of learning rule-based classifiers. The contribution of this paper is an interpretable learning framework IMLI, that is based on maximum satisfiability (MaxSAT) for synthesizing classification rules expressible in proposition logic. Despite the progress of MaxSAT solving in the last decade, the straightforward MaxSAT-based solution cannot scale. Therefore, we incorporate an efficient incremental learning technique inside the MaxSAT formulation by integrating mini-batch learning and iterative rule-learning. In our experiments, IMLI achieves the best balance among prediction accuracy, interpretability, and scalability. As an application, we deploy IMLI in learning popular interpretable classifiers such as decision lists and decision sets.

MLIC: A MaxSAT-Based framework for learning interpretable classification rules

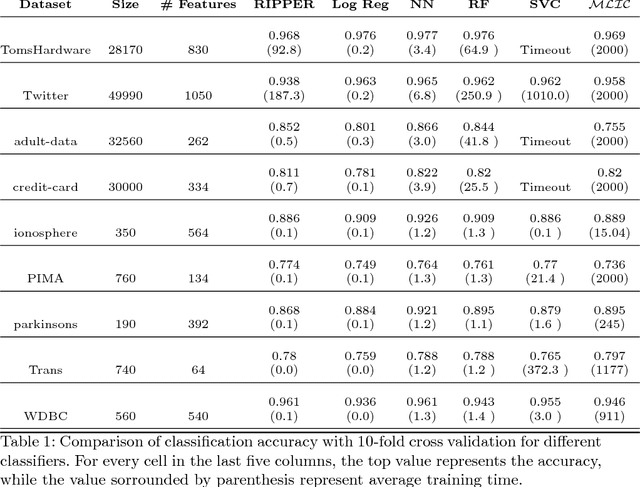
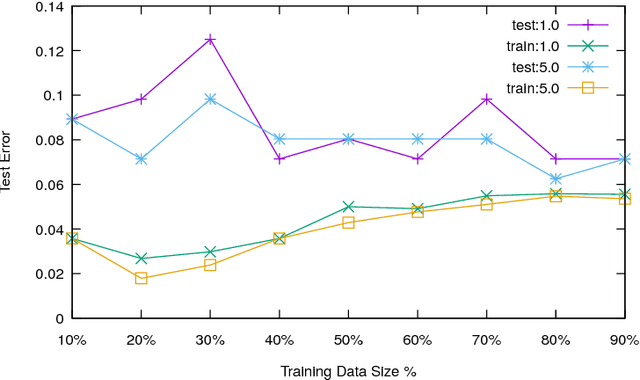
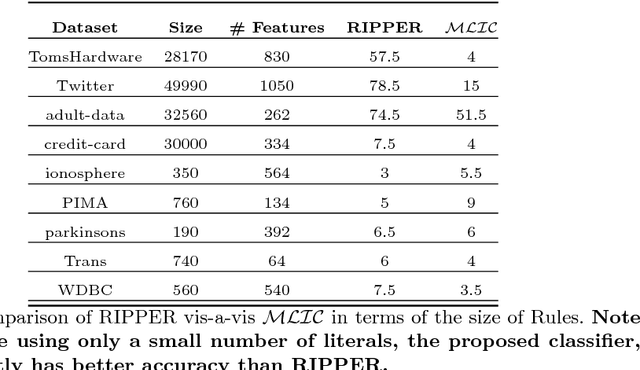
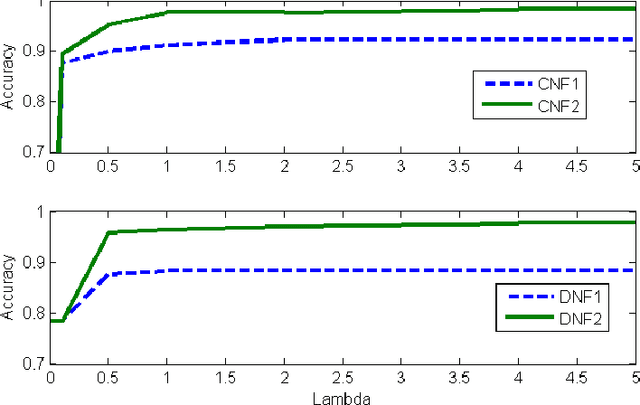
The wide adoption of machine learning approaches in the industry, government, medicine and science has renewed the interest in interpretable machine learning: many decisions are too important to be delegated to black-box techniques such as deep neural networks or kernel SVMs. Historically, problems of learning interpretable classifiers, including classification rules or decision trees, have been approached by greedy heuristic methods as essentially all the exact optimization formulations are NP-hard. Our primary contribution is a MaxSAT-based framework, called MLIC, which allows principled search for interpretable classification rules expressible in propositional logic. Our approach benefits from the revolutionary advances in the constraint satisfaction community to solve large-scale instances of such problems. In experimental evaluations over a collection of benchmarks arising from practical scenarios, we demonstrate its effectiveness: we show that the formulation can solve large classification problems with tens or hundreds of thousands of examples and thousands of features, and to provide a tunable balance of accuracy vs. interpretability. Furthermore, we show that in many problems interpretability can be obtained at only a minor cost in accuracy. The primary objective of the paper is to show that recent advances in the MaxSAT literature make it realistic to find optimal (or very high quality near-optimal) solutions to large-scale classification problems. The key goal of the paper is to excite researchers in both interpretable classification and in the CP community to take it further and propose richer formulations, and to develop bespoke solvers attuned to the problem of interpretable ML.

Quantifying homologous proteins and proteoforms

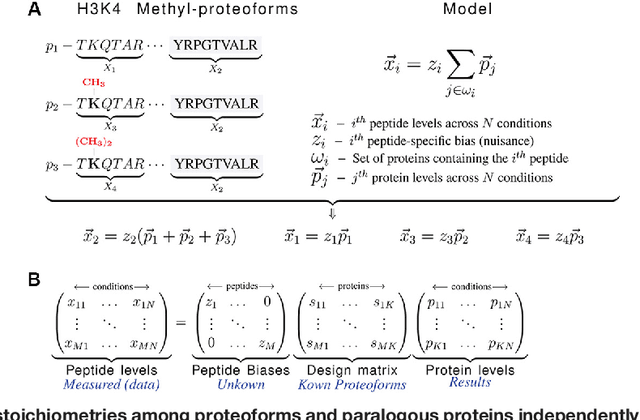
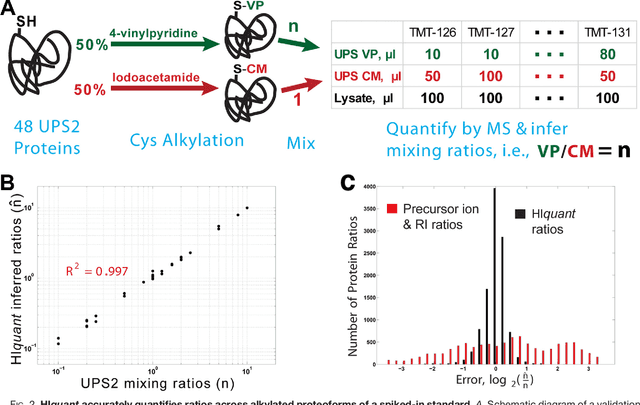
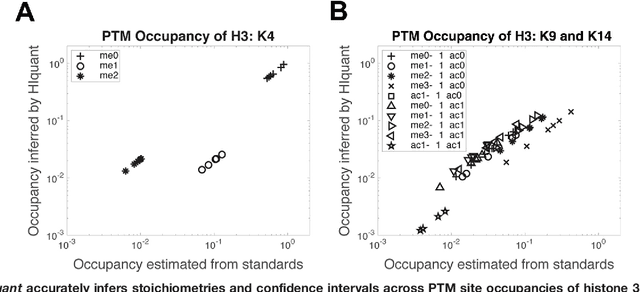
Many proteoforms - arising from alternative splicing, post-translational modifications (PTMs), or paralogous genes - have distinct biological functions, such as histone PTM proteoforms. However, their quantification by existing bottom-up mass-spectrometry (MS) methods is undermined by peptide-specific biases. To avoid these biases, we developed and implemented a first-principles model (HIquant) for quantifying proteoform stoichiometries. We characterized when MS data allow inferring proteoform stoichiometries by HIquant, derived an algorithm for optimal inference, and demonstrated experimentally high accuracy in quantifying fractional PTM occupancy without using external standards, even in the challenging case of the histone modification code. HIquant server is implemented at: https://web.northeastern.edu/slavov/2014_HIquant/

Large-scale Log-determinant Computation through Stochastic Chebyshev Expansions

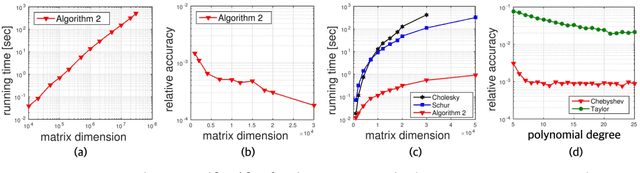
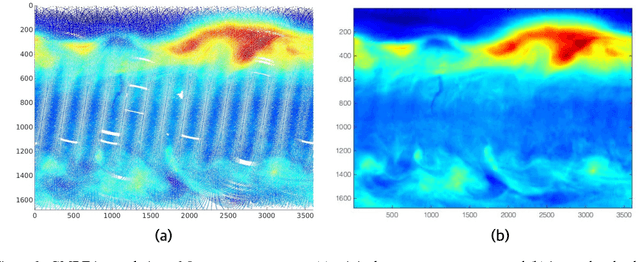
Logarithms of determinants of large positive definite matrices appear ubiquitously in machine learning applications including Gaussian graphical and Gaussian process models, partition functions of discrete graphical models, minimum-volume ellipsoids, metric learning and kernel learning. Log-determinant computation involves the Cholesky decomposition at the cost cubic in the number of variables, i.e., the matrix dimension, which makes it prohibitive for large-scale applications. We propose a linear-time randomized algorithm to approximate log-determinants for very large-scale positive definite and general non-singular matrices using a stochastic trace approximation, called the Hutchinson method, coupled with Chebyshev polynomial expansions that both rely on efficient matrix-vector multiplications. We establish rigorous additive and multiplicative approximation error bounds depending on the condition number of the input matrix. In our experiments, the proposed algorithm can provide very high accuracy solutions at orders of magnitude faster time than the Cholesky decomposition and Schur completion, and enables us to compute log-determinants of matrices involving tens of millions of variables.

Convex Total Least Squares

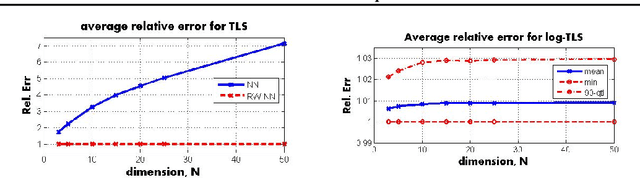
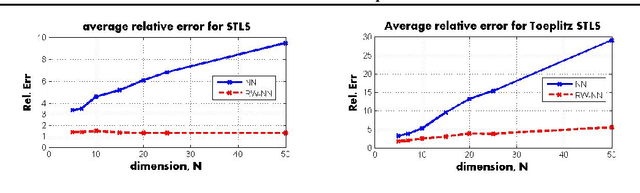
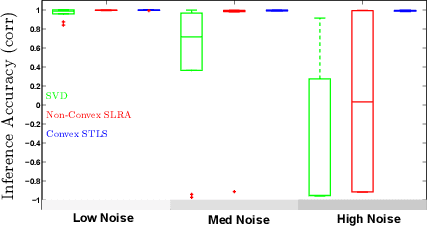
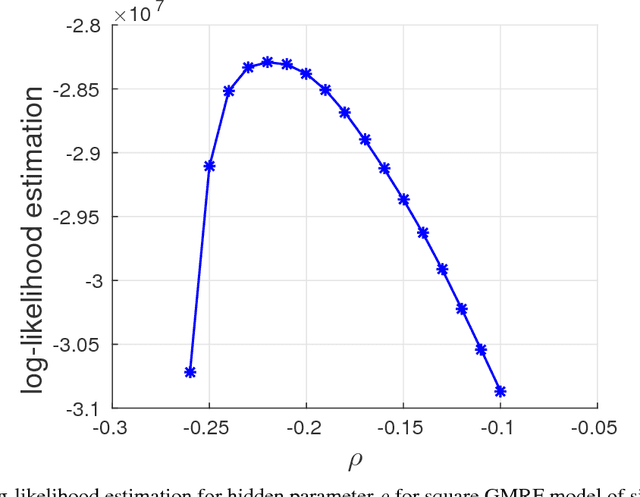
We study the total least squares (TLS) problem that generalizes least squares regression by allowing measurement errors in both dependent and independent variables. TLS is widely used in applied fields including computer vision, system identification and econometrics. The special case when all dependent and independent variables have the same level of uncorrelated Gaussian noise, known as ordinary TLS, can be solved by singular value decomposition (SVD). However, SVD cannot solve many important practical TLS problems with realistic noise structure, such as having varying measurement noise, known structure on the errors, or large outliers requiring robust error-norms. To solve such problems, we develop convex relaxation approaches for a general class of structured TLS (STLS). We show both theoretically and experimentally, that while the plain nuclear norm relaxation incurs large approximation errors for STLS, the re-weighted nuclear norm approach is very effective, and achieves better accuracy on challenging STLS problems than popular non-convex solvers. We describe a fast solution based on augmented Lagrangian formulation, and apply our approach to an important class of biological problems that use population average measurements to infer cell-type and physiological-state specific expression levels that are very hard to measure directly.

Iterative Log Thresholding

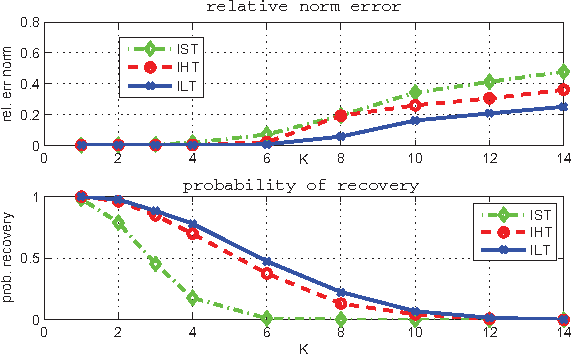
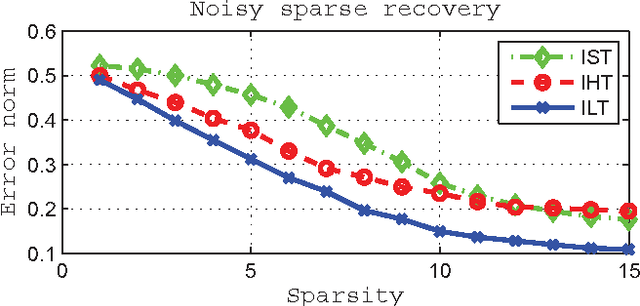
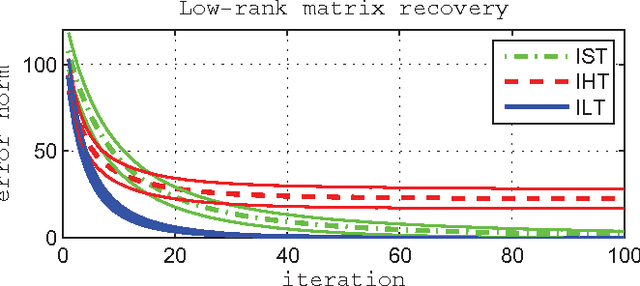
Sparse reconstruction approaches using the re-weighted l1-penalty have been shown, both empirically and theoretically, to provide a significant improvement in recovering sparse signals in comparison to the l1-relaxation. However, numerical optimization of such penalties involves solving problems with l1-norms in the objective many times. Using the direct link of reweighted l1-penalties to the concave log-regularizer for sparsity, we derive a simple prox-like algorithm for the log-regularized formulation. The proximal splitting step of the algorithm has a closed form solution, and we call the algorithm 'log-thresholding' in analogy to soft thresholding for the l1-penalty. We establish convergence results, and demonstrate that log-thresholding provides more accurate sparse reconstructions compared to both soft and hard thresholding. Furthermore, the approach can be directly extended to optimization over matrices with penalty for rank (i.e. the nuclear norm penalty and its re-weigthed version), where we suggest a singular-value log-thresholding approach.