BenchLink: An SoC-Based Benchmark for Resilient Communication Links in GPS-Denied Environments

Accurate timing and synchronization, typically enabled by GPS, are essential for modern wireless communication systems. However, many emerging applications must operate in GPS-denied environments where signals are unreliable or disrupted, resulting in oscillator drift and carrier frequency impairments. To address these challenges, we present BenchLink, a System-on-Chip (SoC)-based benchmark for resilient communication links that functions without GPS and supports adaptive pilot density and modulation. Unlike traditional General Purpose Processor (GPP)-based software-defined radios (e.g. USRPs), the SoC-based design allows for more precise latency control. We implement and evaluate BenchLink on Zynq UltraScale+ MPSoCs, and demonstrate its effectiveness in both ground and aerial environments. A comprehensive dataset has also been collected under various conditions. We will make both the SoC-based link design and dataset available to the wireless community. BenchLink is expected to facilitate future research on data-driven link adaptation, resilient synchronization in GPS-denied scenarios, and emerging applications that require precise latency control, such as integrated radar sensing and communication.

Efficient L1-Norm Principal-Component Analysis via Bit Flipping

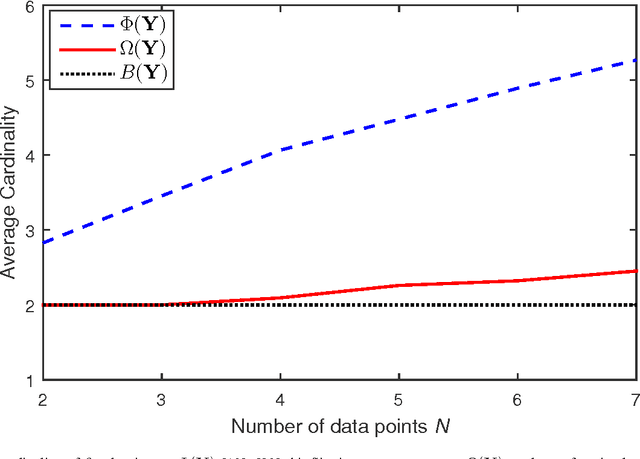
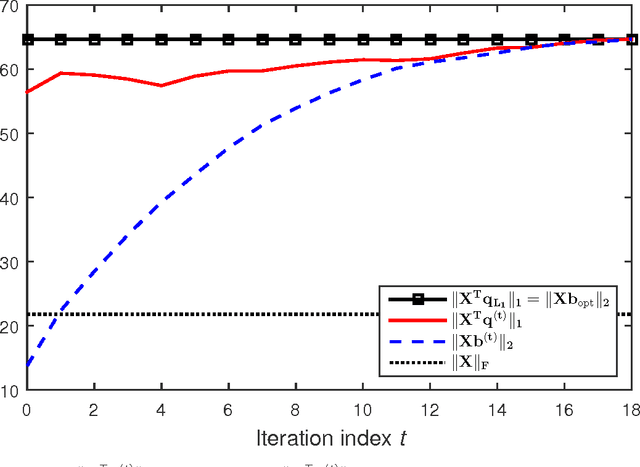
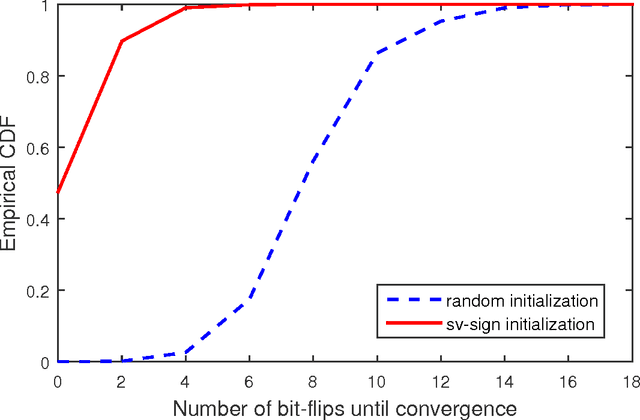
It was shown recently that the $K$ L1-norm principal components (L1-PCs) of a real-valued data matrix $\mathbf X \in \mathbb R^{D \times N}$ ($N$ data samples of $D$ dimensions) can be exactly calculated with cost $\mathcal{O}(2^{NK})$ or, when advantageous, $\mathcal{O}(N^{dK - K + 1})$ where $d=\mathrm{rank}(\mathbf X)$, $K<d$ [1],[2]. In applications where $\mathbf X$ is large (e.g., "big" data of large $N$ and/or "heavy" data of large $d$), these costs are prohibitive. In this work, we present a novel suboptimal algorithm for the calculation of the $K < d$ L1-PCs of $\mathbf X$ of cost $\mathcal O(ND \mathrm{min} \{ N,D\} + N^2(K^4 + dK^2) + dNK^3)$, which is comparable to that of standard (L2-norm) PC analysis. Our theoretical and experimental studies show that the proposed algorithm calculates the exact optimal L1-PCs with high frequency and achieves higher value in the L1-PC optimization metric than any known alternative algorithm of comparable computational cost. The superiority of the calculated L1-PCs over standard L2-PCs (singular vectors) in characterizing potentially faulty data/measurements is demonstrated with experiments on data dimensionality reduction and disease diagnosis from genomic data.

Some Options for L1-Subspace Signal Processing

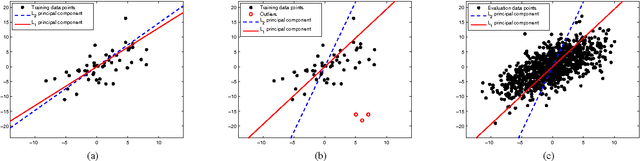
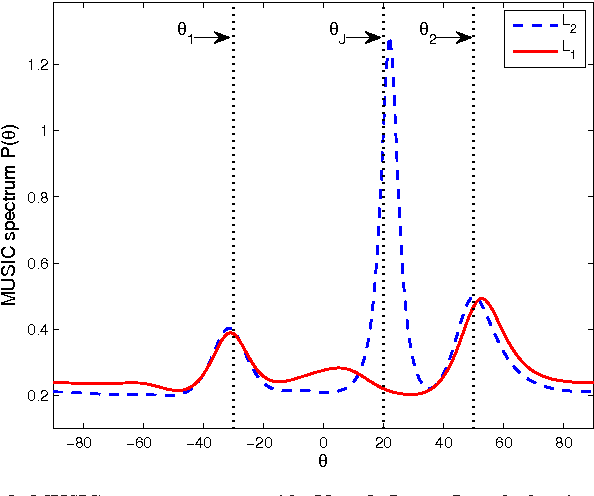
We describe ways to define and calculate $L_1$-norm signal subspaces which are less sensitive to outlying data than $L_2$-calculated subspaces. We focus on the computation of the $L_1$ maximum-projection principal component of a data matrix containing N signal samples of dimension D and conclude that the general problem is formally NP-hard in asymptotically large N, D. We prove, however, that the case of engineering interest of fixed dimension D and asymptotically large sample support N is not and we present an optimal algorithm of complexity $O(N^D)$. We generalize to multiple $L_1$-max-projection components and present an explicit optimal $L_1$ subspace calculation algorithm in the form of matrix nuclear-norm evaluations. We conclude with illustrations of $L_1$-subspace signal processing in the fields of data dimensionality reduction and direction-of-arrival estimation.