Signal-adapted decomposition of graph signals

Analysis of signals defined on complex topologies modeled by graphs is a topic of increasing interest. Signal decomposition plays a crucial role in the representation and processing of such information, in particular, to process graph signals based on notions of scale (e.g., coarse to fine). The graph spectrum is more irregular than for conventional domains; i.e., it is influenced by graph topology, and, therefore, assumptions about spectral representations of graph signals are not easy to make. Here, we propose a tight frame design that is adapted to the graph Laplacian spectral content of given classes of graph signals. The design is based on using the ensemble energy spectral density, a notion of spectral content of given signal sets that we determine either directly using the graph Fourier transform or indirectly through a polynomial-based approximation scheme. The approximation scheme has the benefit that (i) it does not require eigendecomposition of the Laplacian matrix making the method feasible for large graphs, and (ii) it leads to a smooth estimate of the spectral content. A prototype system of spectral kernels each capturing an equal amount of energy is initially defined and subsequently warped using the signal set's ensemble energy spectral density such that the resulting subbands each capture an equal amount of ensemble energy. This approach accounts at the same time for graph topology and signal features, and it provides a meaningful interpretation of subbands in terms of coarse-to-fine representations. We also show how more simplified designs of signal-adapted decomposition of graph signals can be adopted based on ensemble energy estimates. We show the application of proposed methods on the Minnesota road graph and three different designs of brain graphs derived from neuroimaging data.

Hilbert Transform on Graphs: Let There Be Phase

In the past years, many signal processing operations have been successfully adapted to the graph setting. One elegant and effective approach is to exploit the eigendecomposition of a graph shift operator (GSO), such as the adjacency or Laplacian operator, to define a graph Fourier transform when projecting graph signals on the corresponding basis. However, the extension of this scheme to directed graphs is challenging since the associated GSO is non-symmetric and, in general, not diagonalizable. Here, we build upon a recent framework that adds a minimal number of edges to allow diagonalization of the GSO and thus provide a proper graph Fourier transform. We then propose a generalization of the Hilbert transform that leads to a number of simple and elegant recipes to effectively exploit the phase information of graph signals provided by the graph Fourier transform. The feasibility of the approach is demonstrated on several examples.

From Nano to Macro: Overview of the IEEE Bio Image and Signal Processing Technical Committee

The Bio Image and Signal Processing (BISP) Technical Committee (TC) of the IEEE Signal Processing Society (SPS) promotes activities within the broad technical field of biomedical image and signal processing. Areas of interest include medical and biological imaging, digital pathology, molecular imaging, microscopy, and associated computational imaging, image analysis, and image-guided treatment, alongside physiological signal processing, computational biology, and bioinformatics. BISP has 40 members and covers a wide range of EDICS, including CIS-MI: Medical Imaging, BIO-MIA: Medical Image Analysis, BIO-BI: Biological Imaging, BIO: Biomedical Signal Processing, BIO-BCI: Brain/Human-Computer Interfaces, and BIO-INFR: Bioinformatics. BISP plays a central role in the organization of the IEEE International Symposium on Biomedical Imaging (ISBI) and contributes to the technical sessions at the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), and the IEEE International Conference on Image Processing (ICIP). In this paper, we provide a brief history of the TC, review the technological and methodological contributions its community delivered, and highlight promising new directions we anticipate.

Guided Graph Spectral Embedding: Application to the C. elegans Connectome

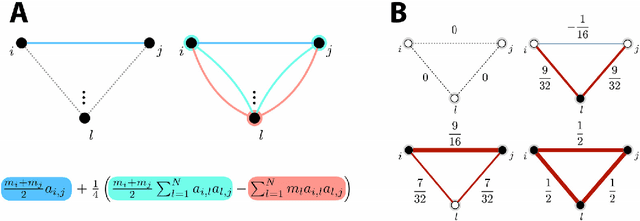
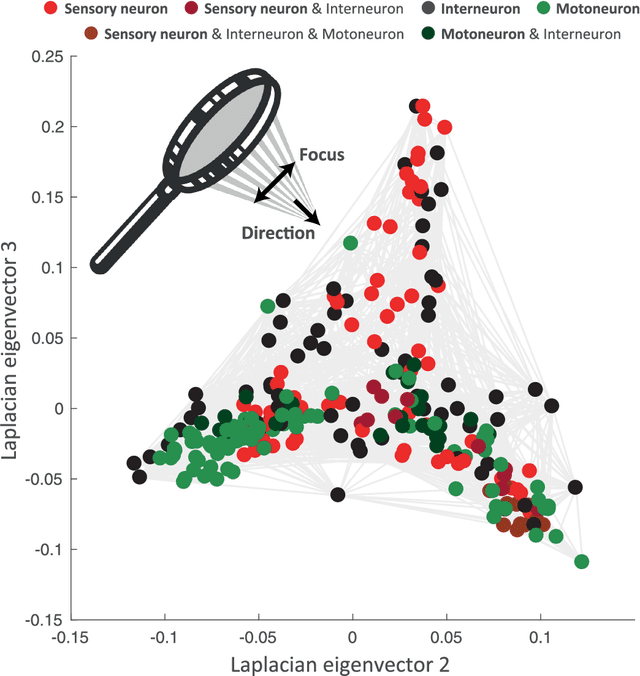
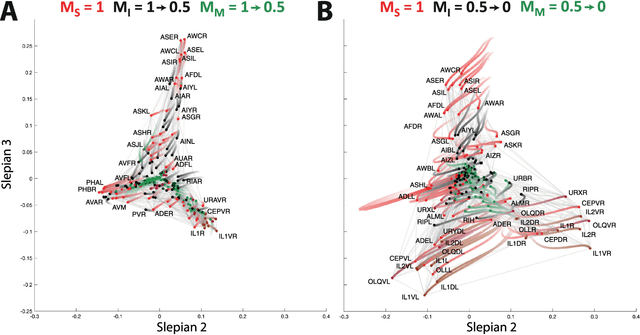
Graph spectral analysis can yield meaningful embeddings of graphs by providing insight into distributed features not directly accessible in nodal domain. Recent efforts in graph signal processing have proposed new decompositions-e.g., based on wavelets and Slepians-that can be applied to filter signals defined on the graph. In this work, we take inspiration from these constructions to define a new guided spectral embedding that combines maximizing energy concentration with minimizing modified embedded distance for a given importance weighting of the nodes. We show these optimization goals are intrinsically opposite, leading to a well-defined and stable spectral decomposition. The importance weighting allows to put the focus on particular nodes and tune the trade-off between global and local effects. Following the derivation of our new optimization criterion and its linear approximation, we exemplify the methodology on the C. elegans structural connectome. The results of our analyses confirm known observations on the nematode's neural network in terms of functionality and importance of cells. Compared to Laplacian embedding, the guided approach, focused on a certain class of cells (sensory, inter- and motoneurons), provides more biological insights, such as the distinction between somatic positions of cells, and their involvement in low or high order processing functions.

Guiding Network Analysis using Graph Slepians: An Illustration for the C. Elegans Connectome

Spectral approaches of network analysis heavily rely upon the eigendecomposition of the graph Laplacian. For instance, in graph signal processing, the Laplacian eigendecomposition is used to define the graph Fourier transform and then transpose signal processing operations to graphs by implementing them in the spectral domain. Here, we build on recent work that generalized Slepian functions to the graph setting. In particular, graph Slepians are band-limited graph signals with maximal energy concentration in a given subgraph. We show how this approach can be used to guide network analysis; i.e., we propose a visualization that reveals network organization of a subgraph, but while striking a balance with global network structure. These developments are illustrated for the structural connectome of the C. Elegans.

When Slepian Meets Fiedler: Putting a Focus on the Graph Spectrum

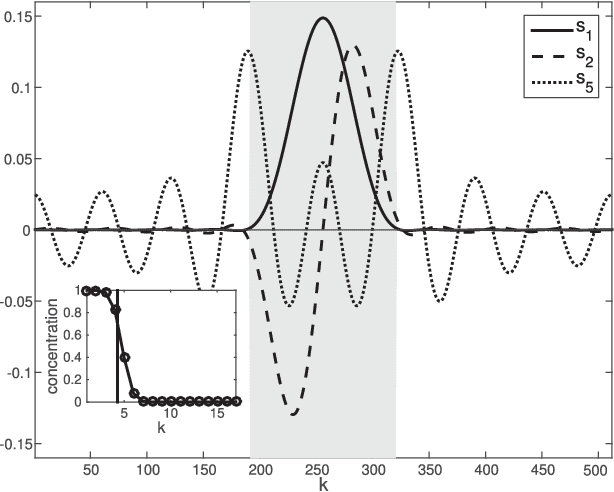
The study of complex systems benefits from graph models and their analysis. In particular, the eigendecomposition of the graph Laplacian lets emerge properties of global organization from local interactions; e.g., the Fiedler vector has the smallest non-zero eigenvalue and plays a key role for graph clustering. Graph signal processing focusses on the analysis of signals that are attributed to the graph nodes. The eigendecomposition of the graph Laplacian allows to define the graph Fourier transform and extend conventional signal-processing operations to graphs. Here, we introduce the design of Slepian graph signals, by maximizing energy concentration in a predefined subgraph for a graph spectral bandlimit. We establish a novel link with classical Laplacian embedding and graph clustering, which provides a meaning to localized graph frequencies.