Decorrelated Adversarial Learning for Age-Invariant Face Recognition

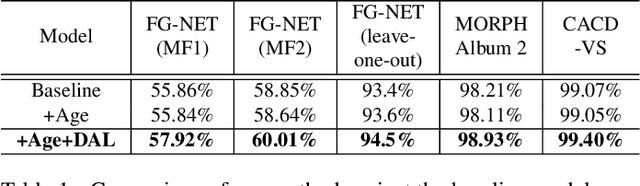
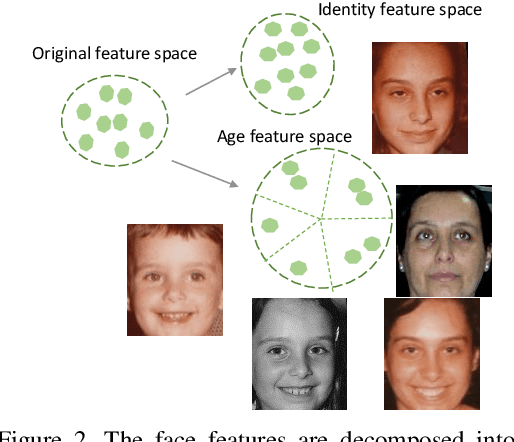
There has been an increasing research interest in age-invariant face recognition. However, matching faces with big age gaps remains a challenging problem, primarily due to the significant discrepancy of face appearances caused by aging. To reduce such a discrepancy, in this paper we propose a novel algorithm to remove age-related components from features mixed with both identity and age information. Specifically, we factorize a mixed face feature into two uncorrelated components: identity-dependent component and age-dependent component, where the identity-dependent component includes information that is useful for face recognition. To implement this idea, we propose the Decorrelated Adversarial Learning (DAL) algorithm, where a Canonical Mapping Module (CMM) is introduced to find the maximum correlation between the paired features generated by a backbone network, while the backbone network and the factorization module are trained to generate features reducing the correlation. Thus, the proposed model learns the decomposed features of age and identity whose correlation is significantly reduced. Simultaneously, the identity-dependent feature and the age-dependent feature are respectively supervised by ID and age preserving signals to ensure that they both contain the correct information. Extensive experiments are conducted on popular public-domain face aging datasets (FG-NET, MORPH Album 2, and CACD-VS) to demonstrate the effectiveness of the proposed approach.

Orthogonal Deep Features Decomposition for Age-Invariant Face Recognition

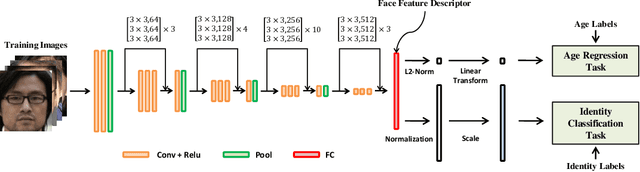
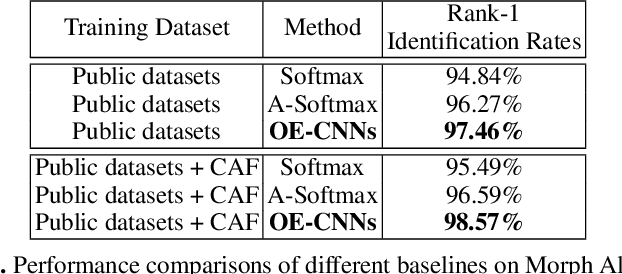
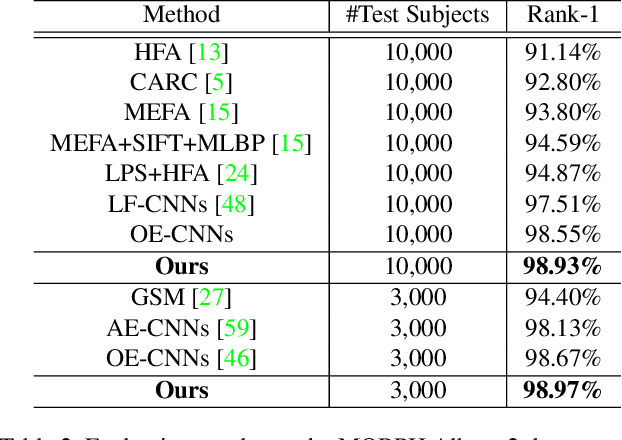
As facial appearance is subject to significant intra-class variations caused by the aging process over time, age-invariant face recognition (AIFR) remains a major challenge in face recognition community. To reduce the intra-class discrepancy caused by the aging, in this paper we propose a novel approach (namely, Orthogonal Embedding CNNs, or OE-CNNs) to learn the age-invariant deep face features. Specifically, we decompose deep face features into two orthogonal components to represent age-related and identity-related features. As a result, identity-related features that are robust to aging are then used for AIFR. Besides, for complementing the existing cross-age datasets and advancing the research in this field, we construct a brand-new large-scale Cross-Age Face dataset (CAF). Extensive experiments conducted on the three public domain face aging datasets (MORPH Album 2, CACD-VS and FG-NET) have shown the effectiveness of the proposed approach and the value of the constructed CAF dataset on AIFR. Benchmarking our algorithm on one of the most popular general face recognition (GFR) dataset LFW additionally demonstrates the comparable generalization performance on GFR.

CosFace: Large Margin Cosine Loss for Deep Face Recognition

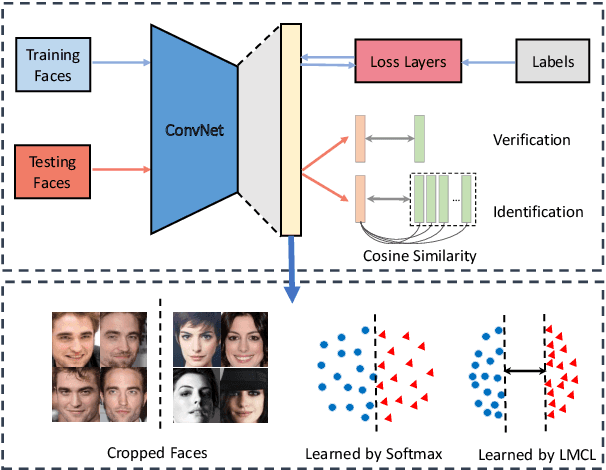
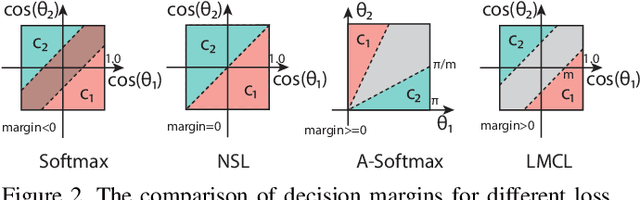
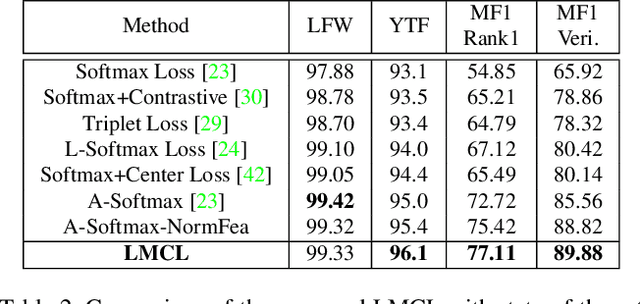
Face recognition has made extraordinary progress owing to the advancement of deep convolutional neural networks (CNNs). The central task of face recognition, including face verification and identification, involves face feature discrimination. However, the traditional softmax loss of deep CNNs usually lacks the power of discrimination. To address this problem, recently several loss functions such as center loss, large margin softmax loss, and angular softmax loss have been proposed. All these improved losses share the same idea: maximizing inter-class variance and minimizing intra-class variance. In this paper, we propose a novel loss function, namely large margin cosine loss (LMCL), to realize this idea from a different perspective. More specifically, we reformulate the softmax loss as a cosine loss by $L_2$ normalizing both features and weight vectors to remove radial variations, based on which a cosine margin term is introduced to further maximize the decision margin in the angular space. As a result, minimum intra-class variance and maximum inter-class variance are achieved by virtue of normalization and cosine decision margin maximization. We refer to our model trained with LMCL as CosFace. Extensive experimental evaluations are conducted on the most popular public-domain face recognition datasets such as MegaFace Challenge, Youtube Faces (YTF) and Labeled Face in the Wild (LFW). We achieve the state-of-the-art performance on these benchmarks, which confirms the effectiveness of our proposed approach.