MEMe: An Accurate Maximum Entropy Method for Efficient Approximations in Large-Scale Machine Learning

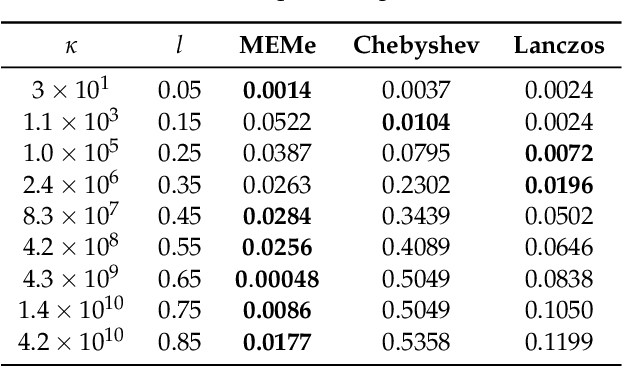
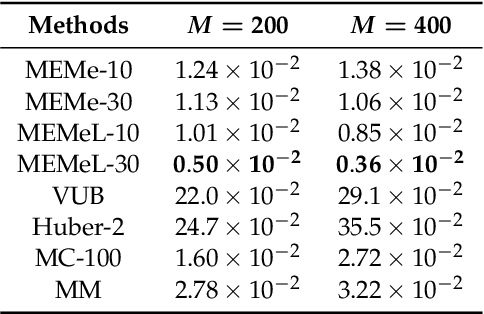
Efficient approximation lies at the heart of large-scale machine learning problems. In this paper, we propose a novel, robust maximum entropy algorithm, which is capable of dealing with hundreds of moments and allows for computationally efficient approximations. We showcase the usefulness of the proposed method, its equivalence to constrained Bayesian variational inference and demonstrate its superiority over existing approaches in two applications, namely, fast log determinant estimation and information-theoretic Bayesian optimisation.

Fast Information-theoretic Bayesian Optimisation

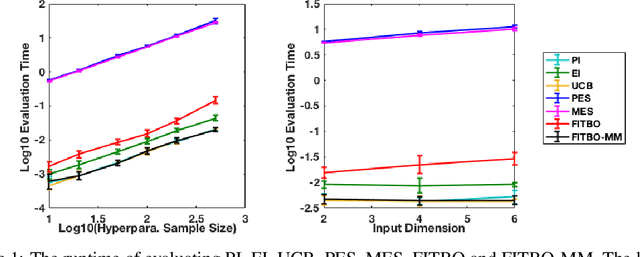
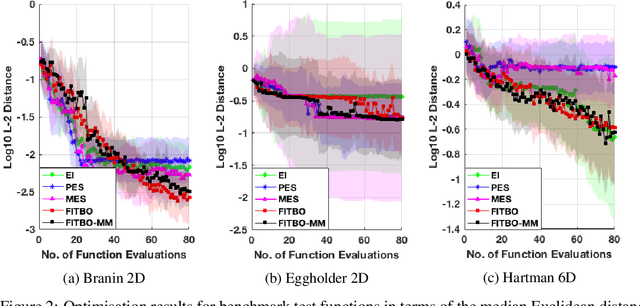
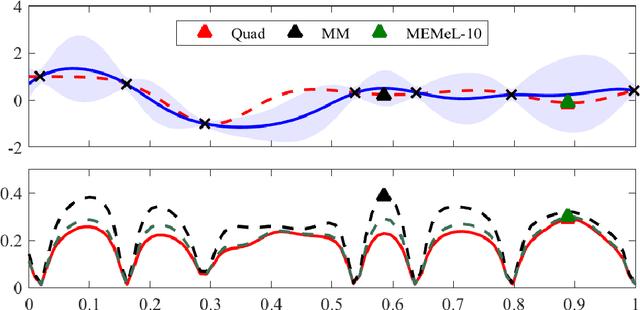
Information-theoretic Bayesian optimisation techniques have demonstrated state-of-the-art performance in tackling important global optimisation problems. However, current information-theoretic approaches require many approximations in implementation, introduce often-prohibitive computational overhead and limit the choice of kernels available to model the objective. We develop a fast information-theoretic Bayesian Optimisation method, FITBO, that avoids the need for sampling the global minimiser, thus significantly reducing computational overhead. Moreover, in comparison with existing approaches, our method faces fewer constraints on kernel choice and enjoys the merits of dealing with the output space. We demonstrate empirically that FITBO inherits the performance associated with information-theoretic Bayesian optimisation, while being even faster than simpler Bayesian optimisation approaches, such as Expected Improvement.

Entropic Spectral Learning in Large Scale Networks

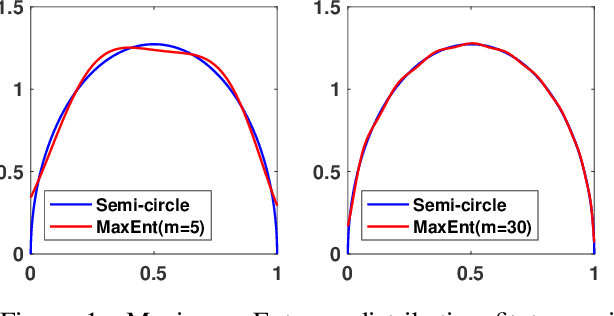
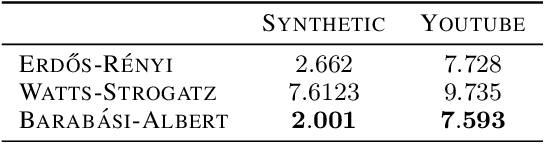
We present a novel algorithm for learning the spectral density of large scale networks using stochastic trace estimation and the method of maximum entropy. The complexity of the algorithm is linear in the number of non-zero elements of the matrix, offering a computational advantage over other algorithms. We apply our algorithm to the problem of community detection in large networks. We show state-of-the-art performance on both synthetic and real datasets.

VBALD - Variational Bayesian Approximation of Log Determinants

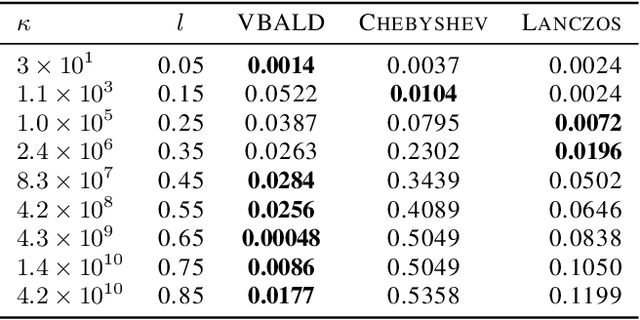
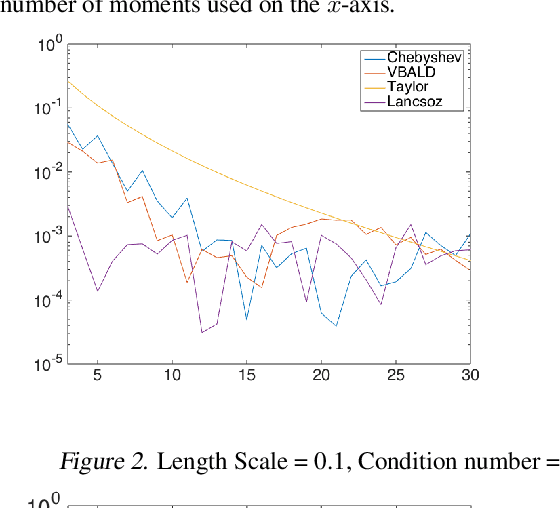
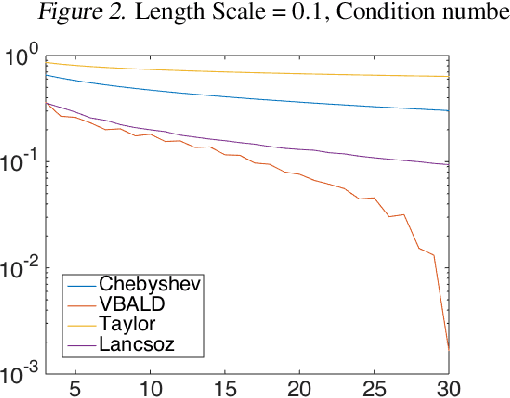
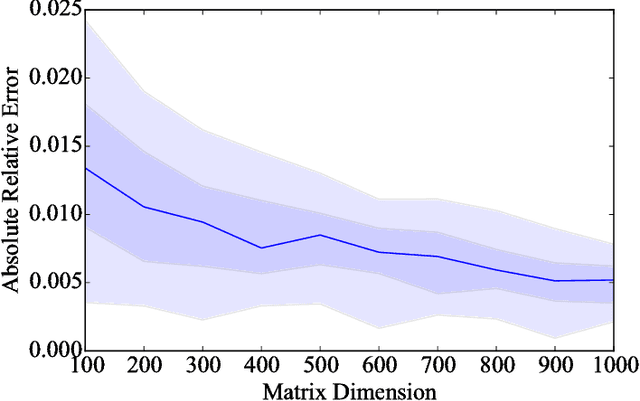
Evaluating the log determinant of a positive definite matrix is ubiquitous in machine learning. Applications thereof range from Gaussian processes, minimum-volume ellipsoids, metric learning, kernel learning, Bayesian neural networks, Determinental Point Processes, Markov random fields to partition functions of discrete graphical models. In order to avoid the canonical, yet prohibitive, Cholesky $\mathcal{O}(n^{3})$ computational cost, we propose a novel approach, with complexity $\mathcal{O}(n^{2})$, based on a constrained variational Bayes algorithm. We compare our method to Taylor, Chebyshev and Lanczos approaches and show state of the art performance on both synthetic and real-world datasets.

Entropic Determinants

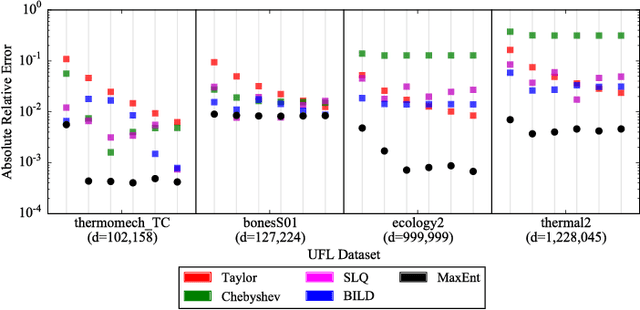
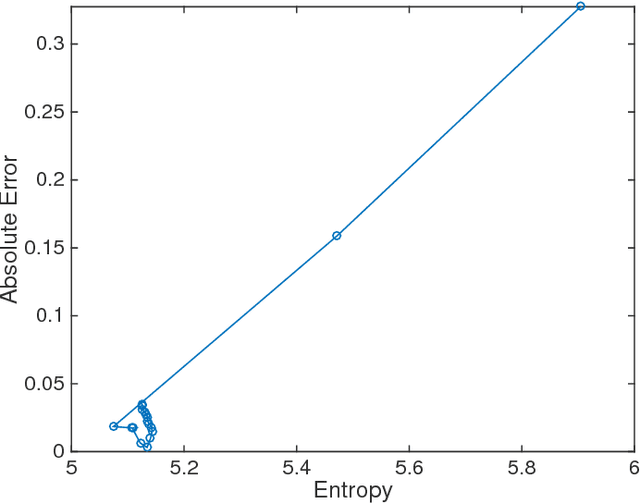
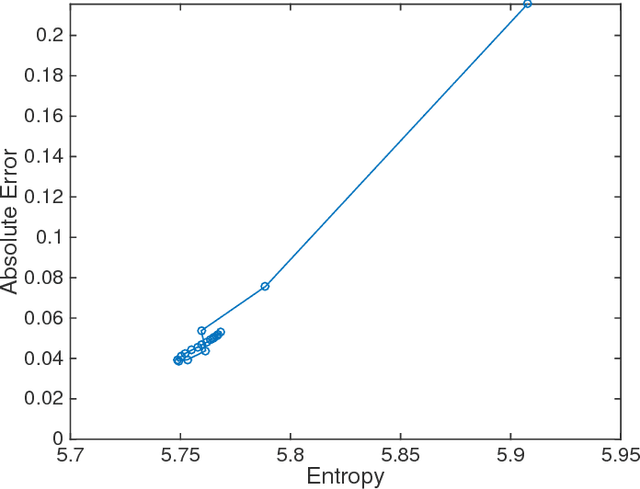
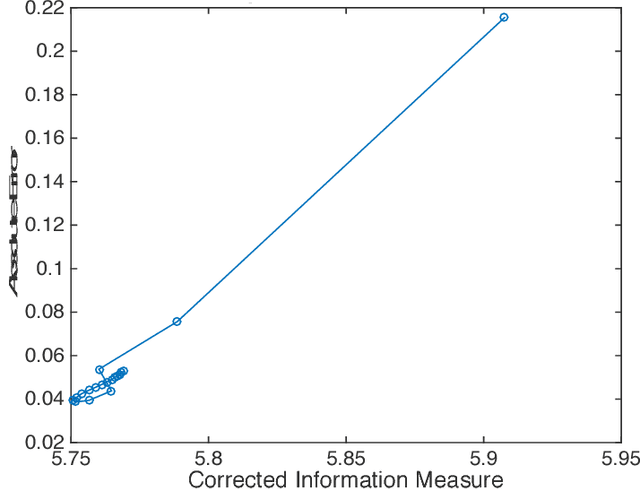
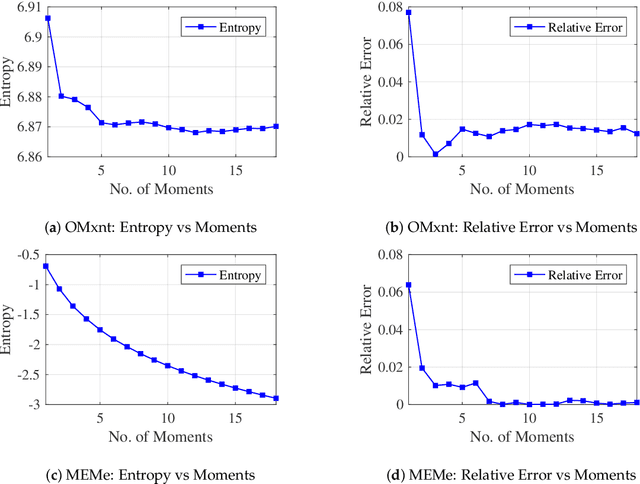
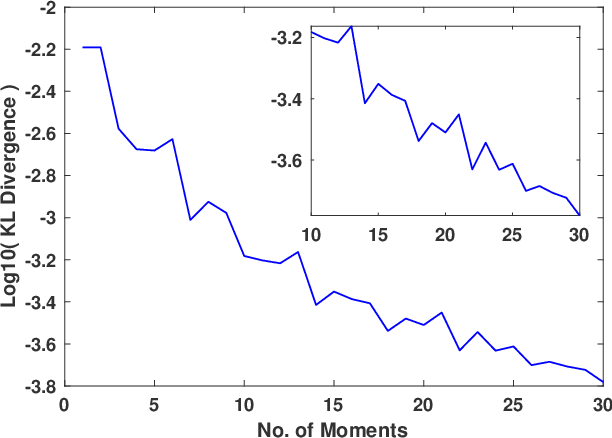
The ability of many powerful machine learning algorithms to deal with large data sets without compromise is often hampered by computationally expensive linear algebra tasks, of which calculating the log determinant is a canonical example. In this paper we demonstrate the optimality of Maximum Entropy methods in approximating such calculations. We prove the equivalence between mean value constraints and sample expectations in the big data limit, that Covariance matrix eigenvalue distributions can be completely defined by moment information and that the reduction of the self entropy of a maximum entropy proposal distribution, achieved by adding more moments reduces the KL divergence between the proposal and true eigenvalue distribution. We empirically verify our results on a variety of SparseSuite matrices and establish best practices.

Entropic Trace Estimates for Log Determinants

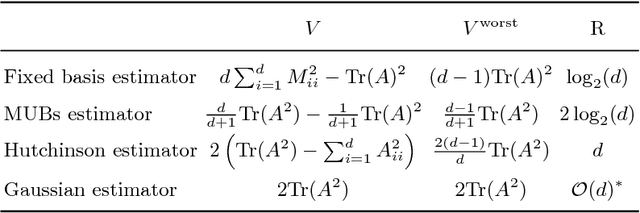
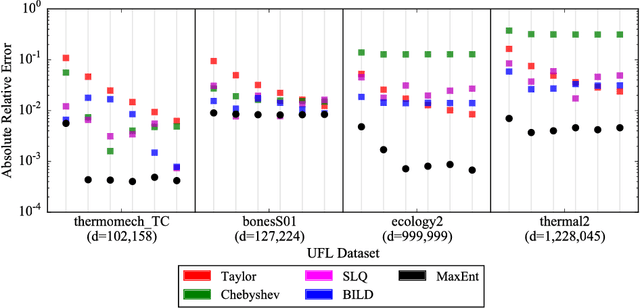
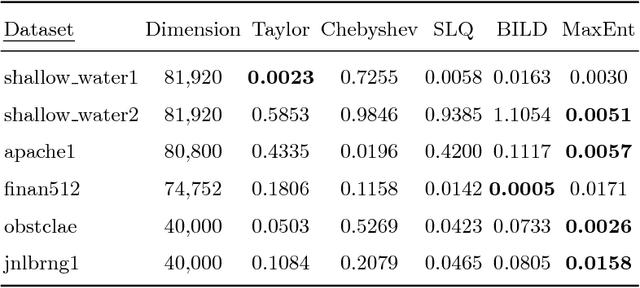
The scalable calculation of matrix determinants has been a bottleneck to the widespread application of many machine learning methods such as determinantal point processes, Gaussian processes, generalised Markov random fields, graph models and many others. In this work, we estimate log determinants under the framework of maximum entropy, given information in the form of moment constraints from stochastic trace estimation. The estimates demonstrate a significant improvement on state-of-the-art alternative methods, as shown on a wide variety of UFL sparse matrices. By taking the example of a general Markov random field, we also demonstrate how this approach can significantly accelerate inference in large-scale learning methods involving the log determinant.