Geometric Attention for Prediction of Differential Properties in 3D Point Clouds

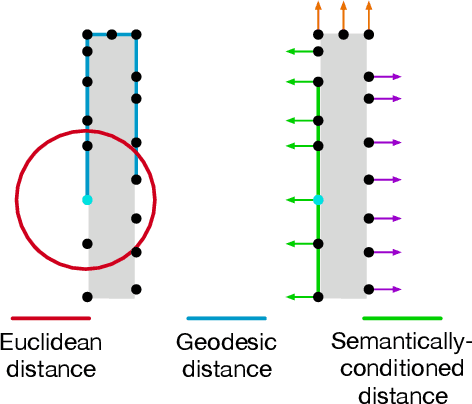
Estimation of differential geometric quantities in discrete 3D data representations is one of the crucial steps in the geometry processing pipeline. Specifically, estimating normals and sharp feature lines from raw point cloud helps improve meshing quality and allows us to use more precise surface reconstruction techniques. When designing a learnable approach to such problems, the main difficulty is selecting neighborhoods in a point cloud and incorporating geometric relations between the points. In this study, we present a geometric attention mechanism that can provide such properties in a learnable fashion. We establish the usefulness of the proposed technique with several experiments on the prediction of normal vectors and the extraction of feature lines.

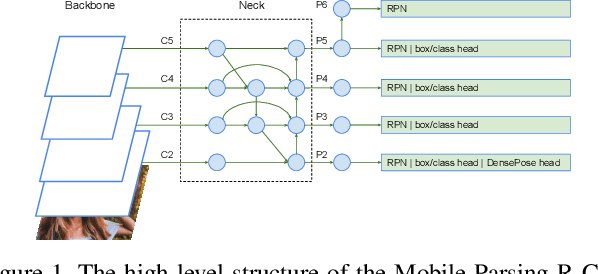
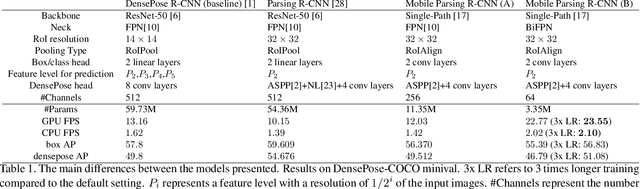
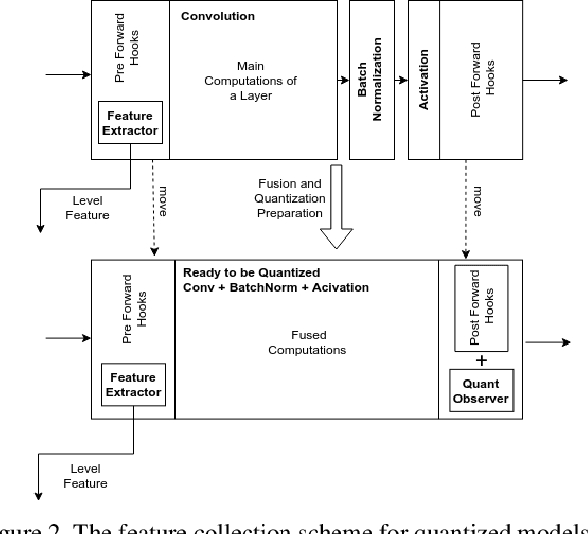
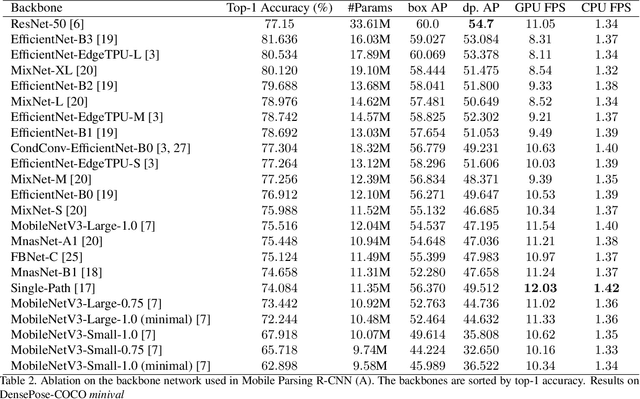
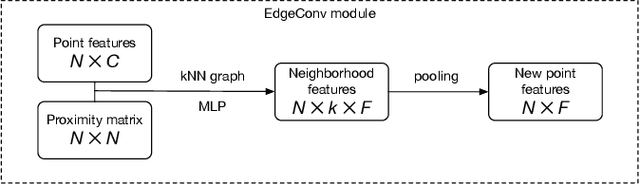
Making DensePose fast and light

DensePose estimation task is a significant step forward for enhancing user experience computer vision applications ranging from augmented reality to cloth fitting. Existing neural network models capable of solving this task are heavily parameterized and a long way from being transferred to an embedded or mobile device. To enable Dense Pose inference on the end device with current models, one needs to support an expensive server-side infrastructure and have a stable internet connection. To make things worse, mobile and embedded devices do not always have a powerful GPU inside. In this work, we target the problem of redesigning the DensePose R-CNN model's architecture so that the final network retains most of its accuracy but becomes more light-weight and fast. To achieve that, we tested and incorporated many deep learning innovations from recent years, specifically performing an ablation study on 23 efficient backbone architectures, multiple two-stage detection pipeline modifications, and custom model quantization methods. As a result, we achieved $17\times$ model size reduction and $2\times$ latency improvement compared to the baseline model.

Neural Splines: Fitting 3D Surfaces with Infinitely-Wide Neural Networks

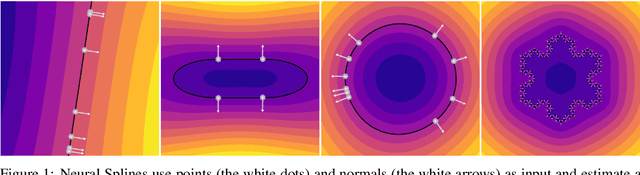
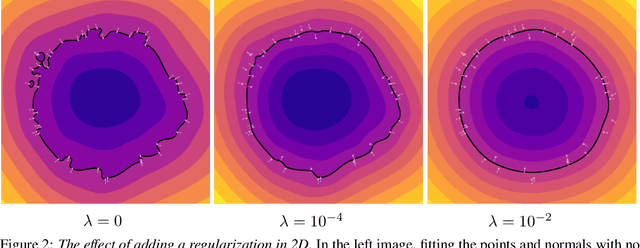
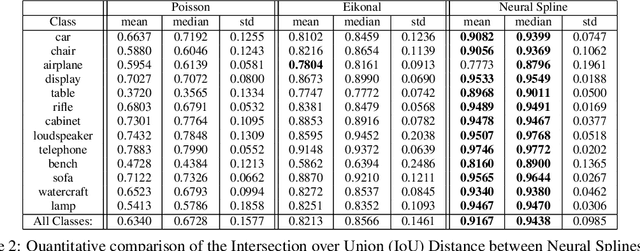
We present Neural Splines, a technique for 3D surface reconstruction that is based on random feature kernels arising from infinitely-wide shallow ReLU networks. Our method achieves state-of-the-art results, outperforming Screened Poisson Surface Reconstruction and modern neural network based techniques. Because our approach is based on a simple kernel formulation, it is fast to run and easy to analyze. We provide explicit analytical expressions for our kernel and argue that our formulation can be seen as a generalization of cubic spline interpolation to higher dimensions. In particular, the RKHS norm associated with our kernel biases toward smooth interpolants. Finally, we formulate Screened Poisson Surface Reconstruction as a kernel method and derive an analytic expression for its norm in the corresponding RKHS.

Latent Video Transformer

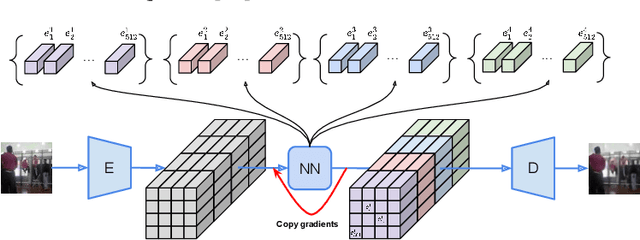
The video generation task can be formulated as a prediction of future video frames given some past frames. Recent generative models for videos face the problem of high computational requirements. Some models require up to 512 Tensor Processing Units for parallel training. In this work, we address this problem via modeling the dynamics in a latent space. After the transformation of frames into the latent space, our model predicts latent representation for the next frames in an autoregressive manner. We demonstrate the performance of our approach on BAIR Robot Pushing and Kinetics-600 datasets. The approach tends to reduce requirements to 8 Graphical Processing Units for training the models while maintaining comparable generation quality.

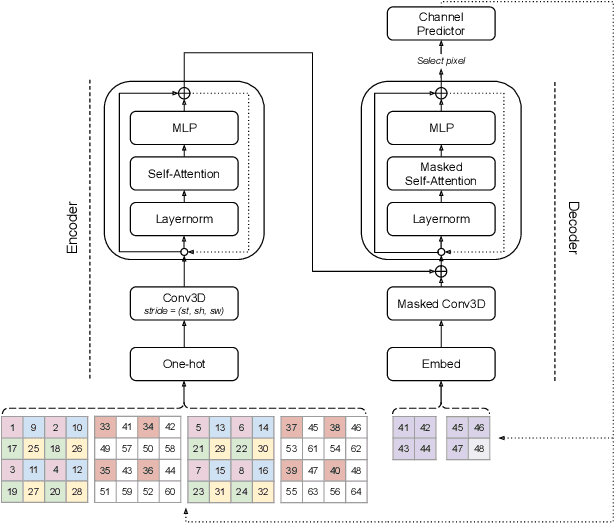
Deep Vectorization of Technical Drawings

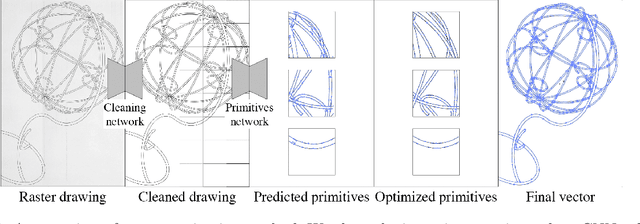
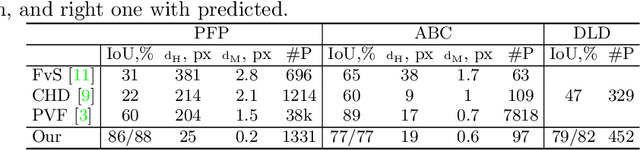
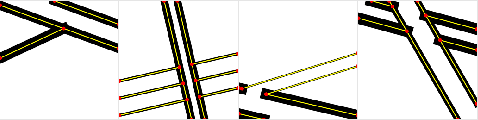
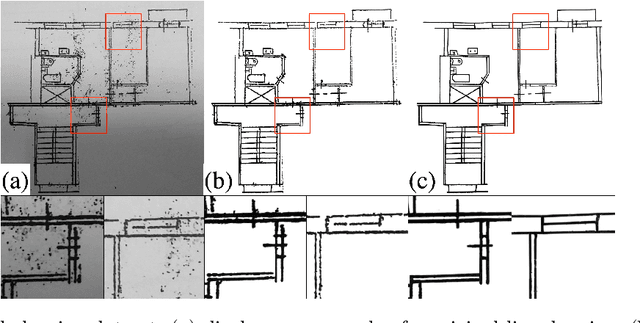
We present a new method for vectorization of technical line drawings, such as floor plans, architectural drawings, and 2D CAD images. Our method includes (1) a deep learning-based cleaning stage to eliminate the background and imperfections in the image and fill in missing parts, (2) a transformer-based network to estimate vector primitives, and (3) optimization procedure to obtain the final primitive configurations. We train the networks on synthetic data, renderings of vector line drawings, and manually vectorized scans of line drawings. Our method quantitatively and qualitatively outperforms a number of existing techniques on a collection of representative technical drawings.

Gradient Dynamics of Shallow Univariate ReLU Networks

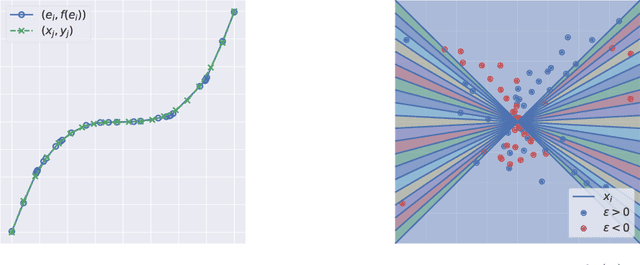
We present a theoretical and empirical study of the gradient dynamics of overparameterized shallow ReLU networks with one-dimensional input, solving least-squares interpolation. We show that the gradient dynamics of such networks are determined by the gradient flow in a non-redundant parameterization of the network function. We examine the principal qualitative features of this gradient flow. In particular, we determine conditions for two learning regimes:kernel and adaptive, which depend both on the relative magnitude of initialization of weights in different layers and the asymptotic behavior of initialization coefficients in the limit of large network widths. We show that learning in the kernel regime yields smooth interpolants, minimizing curvature, and reduces to cubic splines for uniform initializations. Learning in the adaptive regime favors instead linear splines, where knots cluster adaptively at the sample points.

ABC: A Big CAD Model Dataset For Geometric Deep Learning

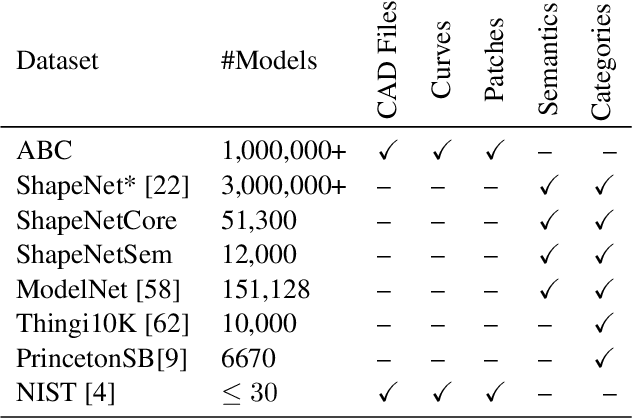
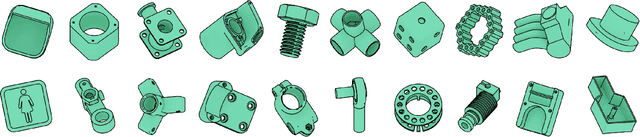
We introduce ABC-Dataset, a collection of one million Computer-Aided Design (CAD) models for research of geometric deep learning methods and applications. Each model is a collection of explicitly parametrized curves and surfaces, providing ground truth for differential quantities, patch segmentation, geometric feature detection, and shape reconstruction. Sampling the parametric descriptions of surfaces and curves allows generating data in different formats and resolutions, enabling fair comparisons for a wide range of geometric learning algorithms. As a use case for our dataset, we perform a large-scale benchmark for estimation of surface normals, comparing existing data driven methods and evaluating their performance against both the ground truth and traditional normal estimation methods.

Deep Geometric Prior for Surface Reconstruction

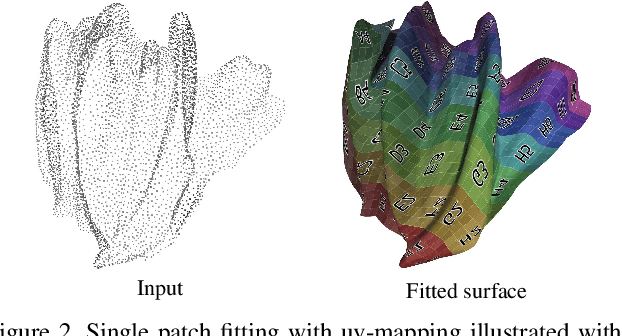
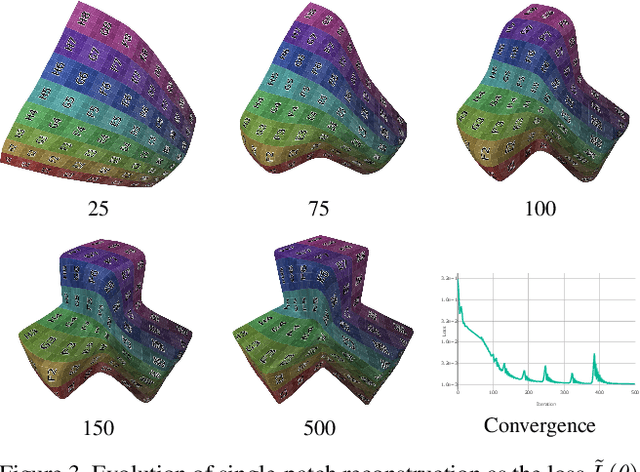
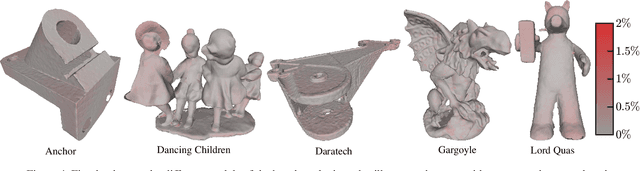
The reconstruction of a discrete surface from a point cloud is a fundamental geometry processing problem that has been studied for decades, with many methods developed. We propose the use of a deep neural network as a geometric prior for surface reconstruction. Specifically, we overfit a neural network representing a local chart parameterization to part of an input point cloud using the Wasserstein distance as a measure of approximation. By jointly fitting many such networks to overlapping parts of the point cloud, while enforcing a consistency condition, we compute a manifold atlas. By sampling this atlas, we can produce a dense reconstruction of the surface approximating the input cloud. The entire procedure does not require any training data or explicit regularization, yet, we show that it is able to perform remarkably well: not introducing typical overfitting artifacts, and approximating sharp features closely at the same time. We experimentally show that this geometric prior produces good results for both man-made objects containing sharp features and smoother organic objects, as well as noisy inputs. We compare our method with a number of well-known reconstruction methods on a standard surface reconstruction benchmark.

Surface Networks

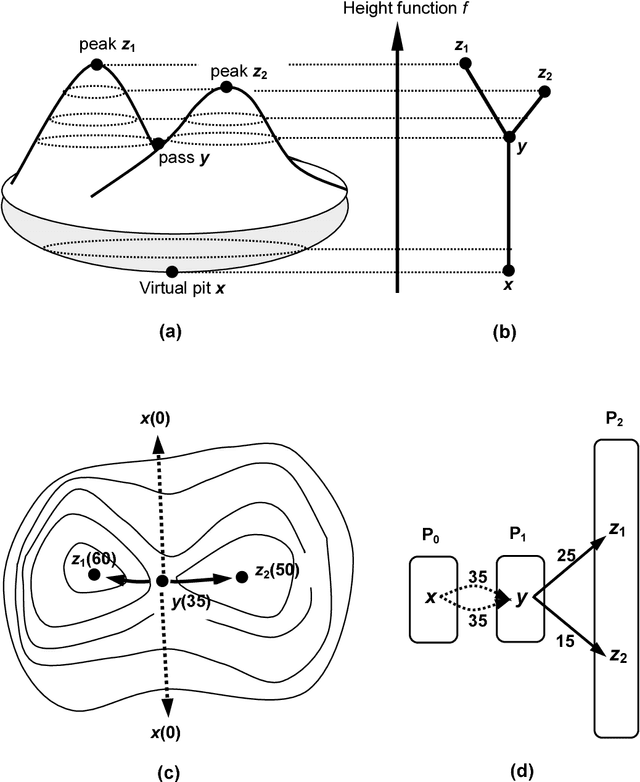
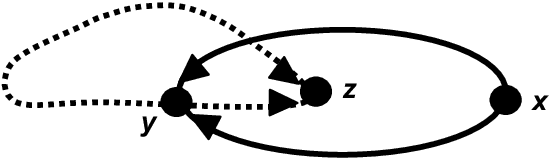
We study data-driven representations for three-dimensional triangle meshes, which are one of the prevalent objects used to represent 3D geometry. Recent works have developed models that exploit the intrinsic geometry of manifolds and graphs, namely the Graph Neural Networks (GNNs) and its spectral variants, which learn from the local metric tensor via the Laplacian operator. Despite offering excellent sample complexity and built-in invariances, intrinsic geometry alone is invariant to isometric deformations, making it unsuitable for many applications. To overcome this limitation, we propose several upgrades to GNNs to leverage extrinsic differential geometry properties of three-dimensional surfaces, increasing its modeling power. In particular, we propose to exploit the Dirac operator, whose spectrum detects principal curvature directions --- this is in stark contrast with the classical Laplace operator, which directly measures mean curvature. We coin the resulting models \emph{Surface Networks (SN)}. We prove that these models define shape representations that are stable to deformation and to discretization, and we demonstrate the efficiency and versatility of SNs on two challenging tasks: temporal prediction of mesh deformations under non-linear dynamics and generative models using a variational autoencoder framework with encoders/decoders given by SNs.