Online Structured Laplace Approximations For Overcoming Catastrophic Forgetting

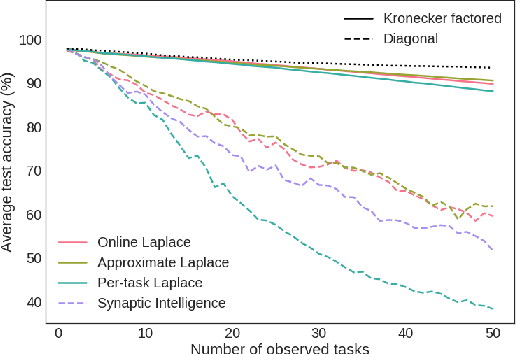
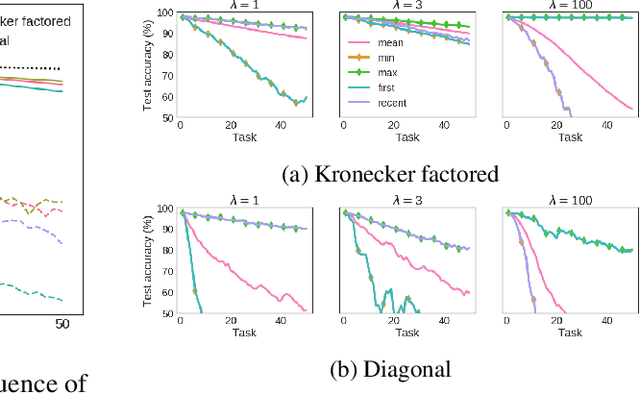
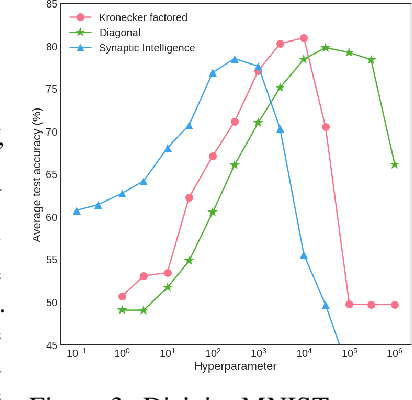
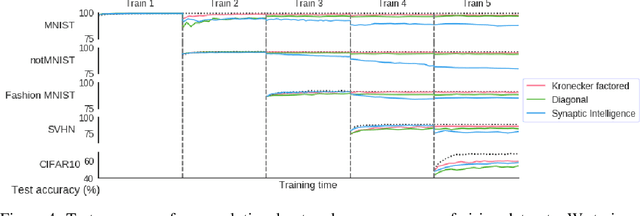
We introduce the Kronecker factored online Laplace approximation for overcoming catastrophic forgetting in neural networks. The method is grounded in a Bayesian online learning framework, where we recursively approximate the posterior after every task with a Gaussian, leading to a quadratic penalty on changes to the weights. The Laplace approximation requires calculating the Hessian around a mode, which is typically intractable for modern architectures. In order to make our method scalable, we leverage recent block-diagonal Kronecker factored approximations to the curvature. Our algorithm achieves over 90% test accuracy across a sequence of 50 instantiations of the permuted MNIST dataset, substantially outperforming related methods for overcoming catastrophic forgetting.

Wider and Deeper, Cheaper and Faster: Tensorized LSTMs for Sequence Learning

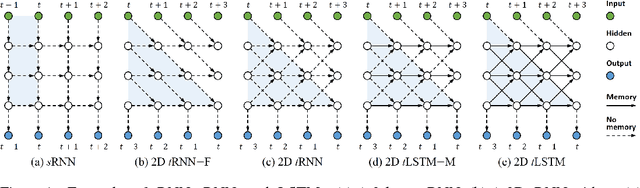
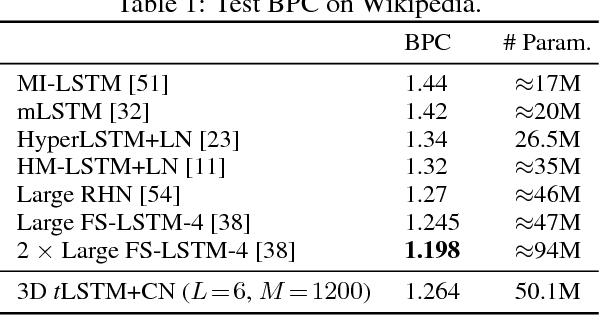
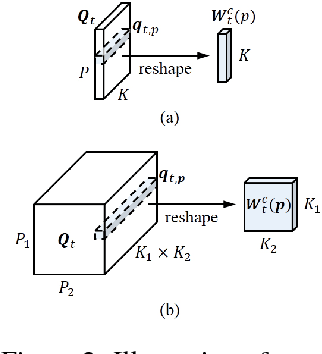
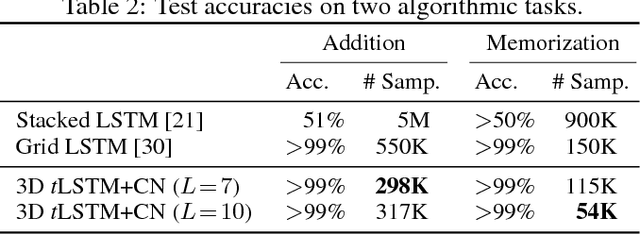
Long Short-Term Memory (LSTM) is a popular approach to boosting the ability of Recurrent Neural Networks to store longer term temporal information. The capacity of an LSTM network can be increased by widening and adding layers. However, usually the former introduces additional parameters, while the latter increases the runtime. As an alternative we propose the Tensorized LSTM in which the hidden states are represented by tensors and updated via a cross-layer convolution. By increasing the tensor size, the network can be widened efficiently without additional parameters since the parameters are shared across different locations in the tensor; by delaying the output, the network can be deepened implicitly with little additional runtime since deep computations for each timestep are merged into temporal computations of the sequence. Experiments conducted on five challenging sequence learning tasks show the potential of the proposed model.

Thinking Fast and Slow with Deep Learning and Tree Search

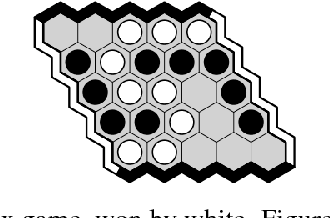
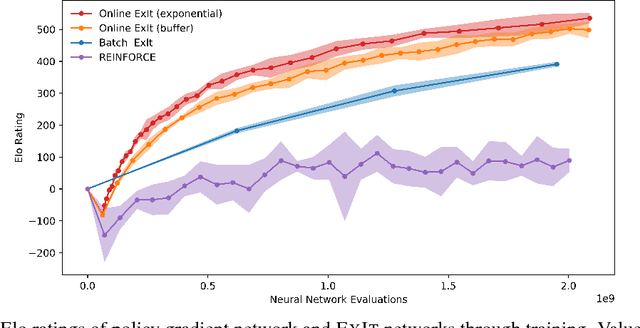
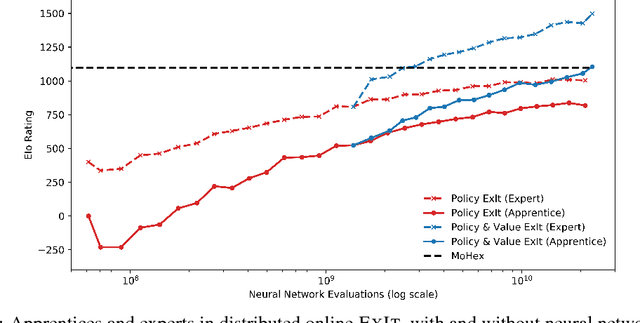
Sequential decision making problems, such as structured prediction, robotic control, and game playing, require a combination of planning policies and generalisation of those plans. In this paper, we present Expert Iteration (ExIt), a novel reinforcement learning algorithm which decomposes the problem into separate planning and generalisation tasks. Planning new policies is performed by tree search, while a deep neural network generalises those plans. Subsequently, tree search is improved by using the neural network policy to guide search, increasing the strength of new plans. In contrast, standard deep Reinforcement Learning algorithms rely on a neural network not only to generalise plans, but to discover them too. We show that ExIt outperforms REINFORCE for training a neural network to play the board game Hex, and our final tree search agent, trained tabula rasa, defeats MoHex 1.0, the most recent Olympiad Champion player to be publicly released.

Practical Gauss-Newton Optimisation for Deep Learning

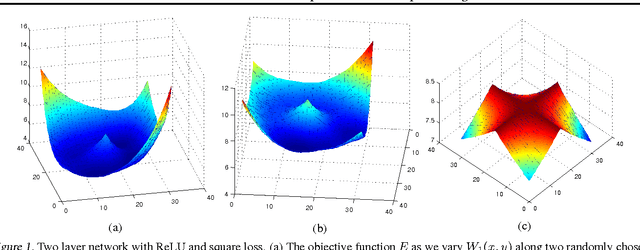
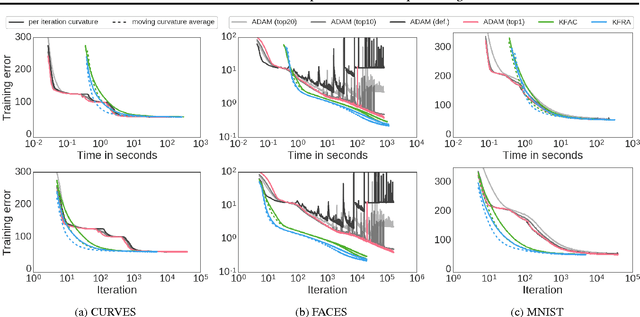
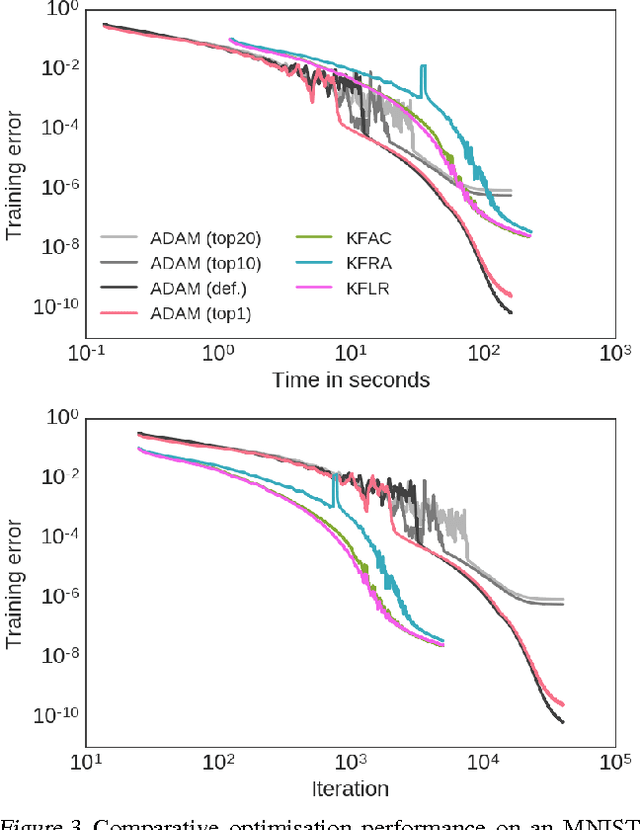
We present an efficient block-diagonal ap- proximation to the Gauss-Newton matrix for feedforward neural networks. Our result- ing algorithm is competitive against state- of-the-art first order optimisation methods, with sometimes significant improvement in optimisation performance. Unlike first-order methods, for which hyperparameter tuning of the optimisation parameters is often a labo- rious process, our approach can provide good performance even when used with default set- tings. A side result of our work is that for piecewise linear transfer functions, the net- work objective function can have no differ- entiable local maxima, which may partially explain why such transfer functions facilitate effective optimisation.

Nesterov's Accelerated Gradient and Momentum as approximations to Regularised Update Descent

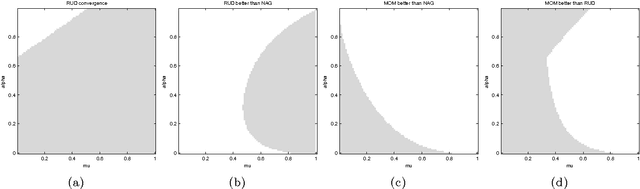
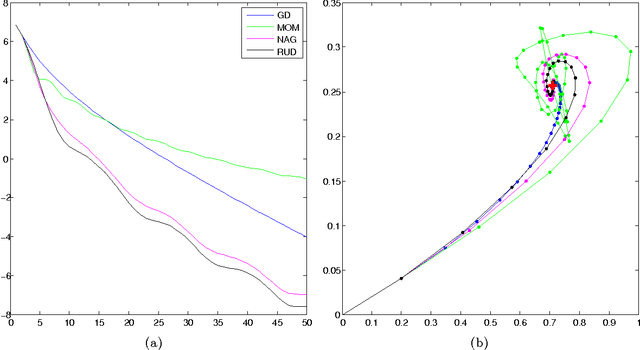
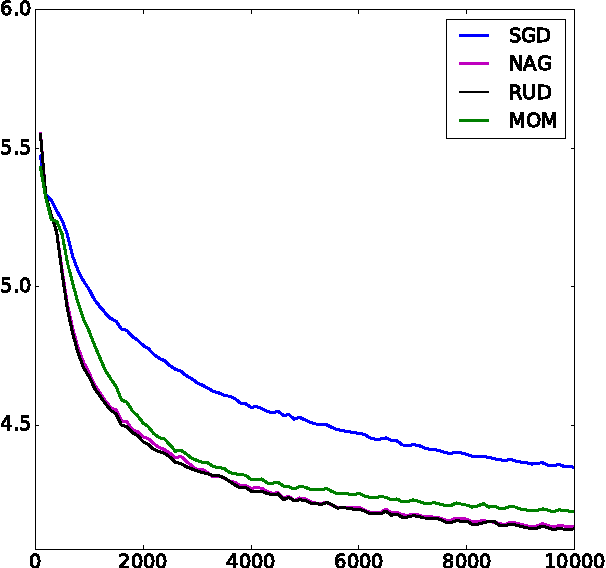
We present a unifying framework for adapting the update direction in gradient-based iterative optimization methods. As natural special cases we re-derive classical momentum and Nesterov's accelerated gradient method, lending a new intuitive interpretation to the latter algorithm. We show that a new algorithm, which we term Regularised Gradient Descent, can converge more quickly than either Nesterov's algorithm or the classical momentum algorithm.

Dealing with a large number of classes -- Likelihood, Discrimination or Ranking?

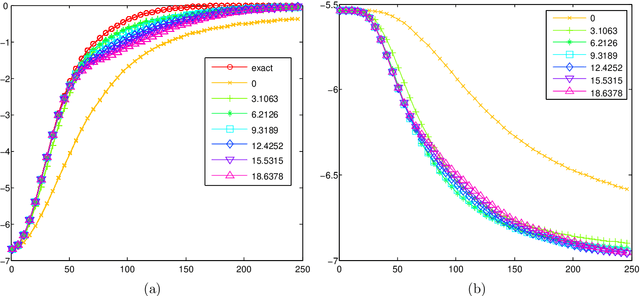
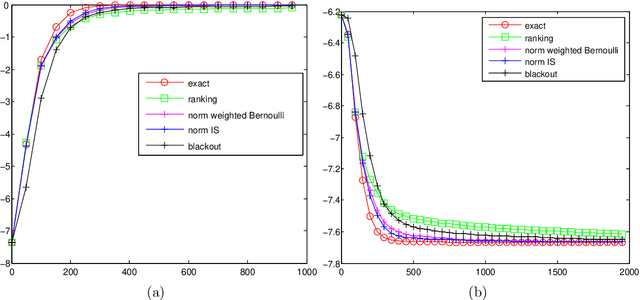
We consider training probabilistic classifiers in the case of a large number of classes. The number of classes is assumed too large to perform exact normalisation over all classes. To account for this we consider a simple approach that directly approximates the likelihood. We show that this simple approach works well on toy problems and is competitive with recently introduced alternative non-likelihood based approximations. Furthermore, we relate this approach to a simple ranking objective. This leads us to suggest a specific setting for the optimal threshold in the ranking objective.

On solving Ordinary Differential Equations using Gaussian Processes

We describe a set of Gaussian Process based approaches that can be used to solve non-linear Ordinary Differential Equations. We suggest an explicit probabilistic solver and two implicit methods, one analogous to Picard iteration and the other to gradient matching. All methods have greater accuracy than previously suggested Gaussian Process approaches. We also suggest a general approach that can yield error estimates from any standard ODE solver.

Variational Optimization

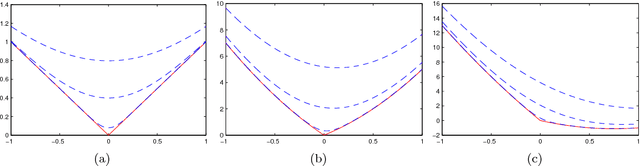
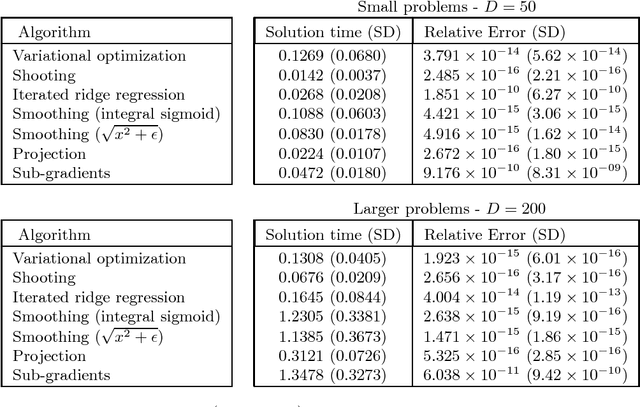
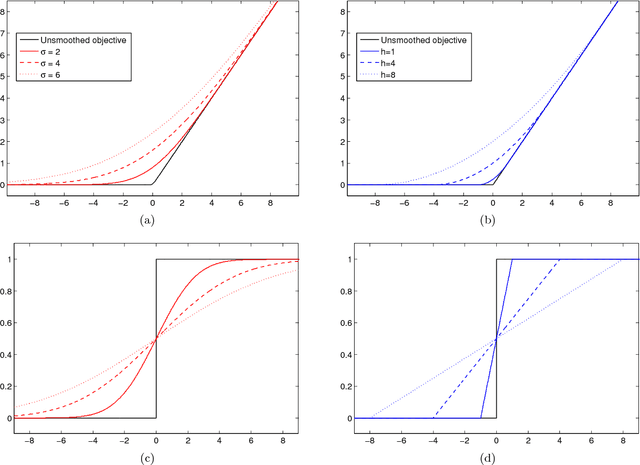
We discuss a general technique that can be used to form a differentiable bound on the optima of non-differentiable or discrete objective functions. We form a unified description of these methods and consider under which circumstances the bound is concave. In particular we consider two concrete applications of the method, namely sparse learning and support vector classification.

On the Computational Complexity of Stochastic Controller Optimization in POMDPs

We show that the problem of finding an optimal stochastic 'blind' controller in a Markov decision process is an NP-hard problem. The corresponding decision problem is NP-hard, in PSPACE, and SQRT-SUM-hard, hence placing it in NP would imply breakthroughs in long-standing open problems in computer science. Our result establishes that the more general problem of stochastic controller optimization in POMDPs is also NP-hard. Nonetheless, we outline a special case that is convex and admits efficient global solutions.

Bayesian Conditional Cointegration

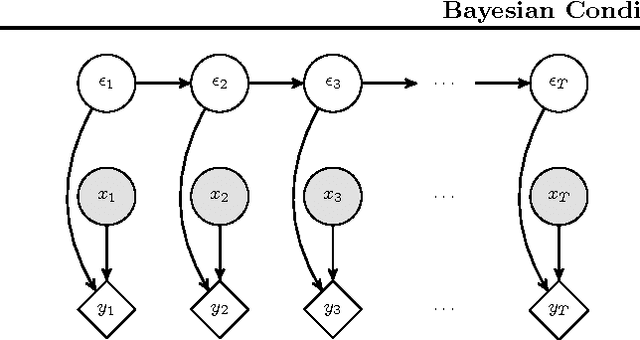
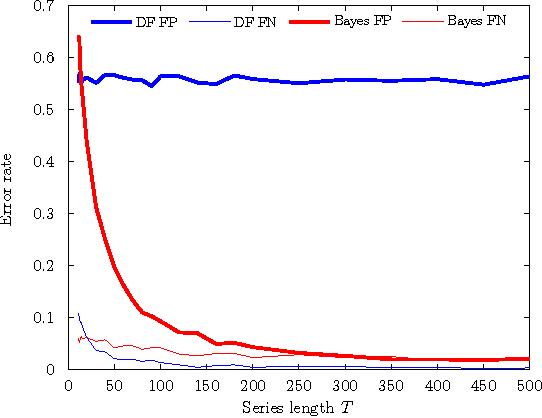
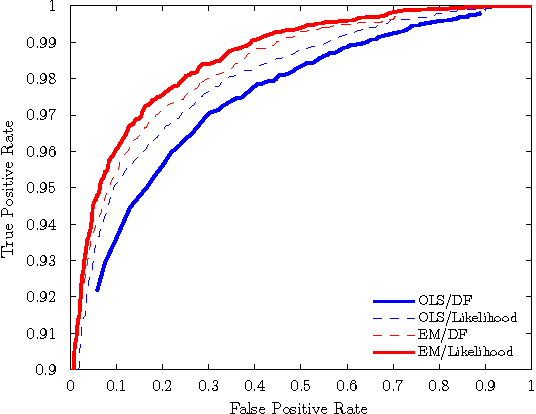
Cointegration is an important topic for time-series, and describes a relationship between two series in which a linear combination is stationary. Classically, the test for cointegration is based on a two stage process in which first the linear relation between the series is estimated by Ordinary Least Squares. Subsequently a unit root test is performed on the residuals. A well-known deficiency of this classical approach is that it can lead to erroneous conclusions about the presence of cointegration. As an alternative, we present a framework for estimating whether cointegration exists using Bayesian inference which is empirically superior to the classical approach. Finally, we apply our technique to model segmented cointegration in which cointegration may exist only for limited time. In contrast to previous approaches our model makes no restriction on the number of possible cointegration segments.