Chris Bracegirdle
University College London
Bayesian Conditional Cointegration
Jun 27, 2012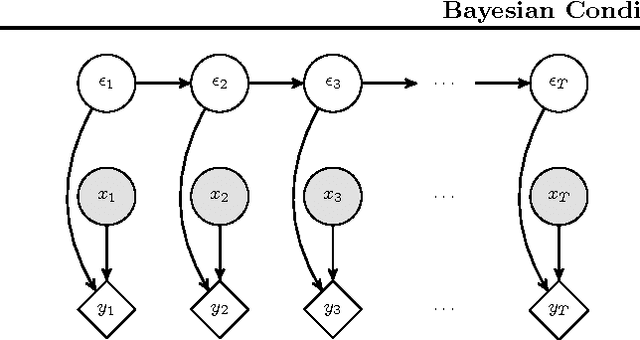

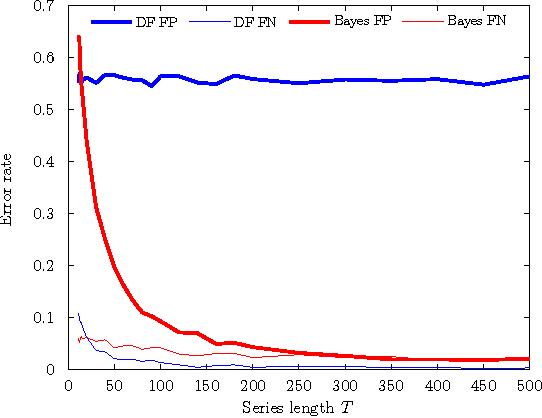
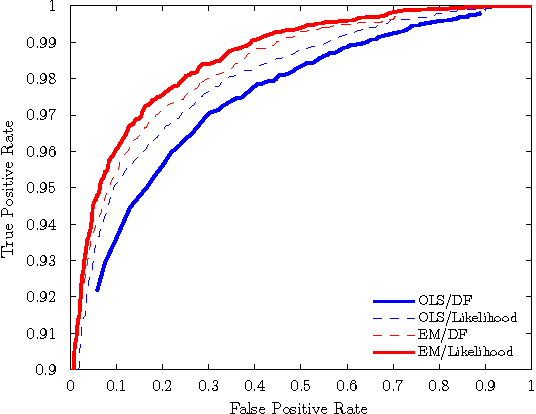
Abstract:Cointegration is an important topic for time-series, and describes a relationship between two series in which a linear combination is stationary. Classically, the test for cointegration is based on a two stage process in which first the linear relation between the series is estimated by Ordinary Least Squares. Subsequently a unit root test is performed on the residuals. A well-known deficiency of this classical approach is that it can lead to erroneous conclusions about the presence of cointegration. As an alternative, we present a framework for estimating whether cointegration exists using Bayesian inference which is empirically superior to the classical approach. Finally, we apply our technique to model segmented cointegration in which cointegration may exist only for limited time. In contrast to previous approaches our model makes no restriction on the number of possible cointegration segments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge