A Kernel-based Resource-efficient Neural Surrogate for Multi-fidelity Prediction of Aerodynamic Field

Surrogate models provide fast alternatives to costly aerodynamic simulations and are extremely useful in design and optimization applications. This study proposes the use of a recent kernel-based neural surrogate, KHRONOS. In this work, we blend sparse high-fidelity (HF) data with low-fidelity (LF) information to predict aerodynamic fields under varying constraints in computational resources. Unlike traditional approaches, KHRONOS is built upon variational principles, interpolation theory, and tensor decomposition. These elements provide a mathematical basis for heavy pruning compared to dense neural networks. Using the AirfRANS dataset as a high-fidelity benchmark and NeuralFoil to generate low-fidelity counterparts, this work compares the performance of KHRONOS with three contemporary model architectures: a multilayer perceptron (MLP), a graph neural network (GNN), and a physics-informed neural network (PINN). We consider varying levels of high-fidelity data availability (0%, 10%, and 30%) and increasingly complex geometry parameterizations. These are used to predict the surface pressure coefficient distribution over the airfoil. Results indicate that, whilst all models eventually achieve comparable predictive accuracy, KHRONOS excels in resource-constrained conditions. In this domain, KHRONOS consistently requires orders of magnitude fewer trainable parameters and delivers much faster training and inference than contemporary dense neural networks at comparable accuracy. These findings highlight the potential of KHRONOS and similar architectures to balance accuracy and efficiency in multi-fidelity aerodynamic field prediction.

Manifold Alignment-Based Multi-Fidelity Reduced-Order Modeling Applied to Structural Analysis

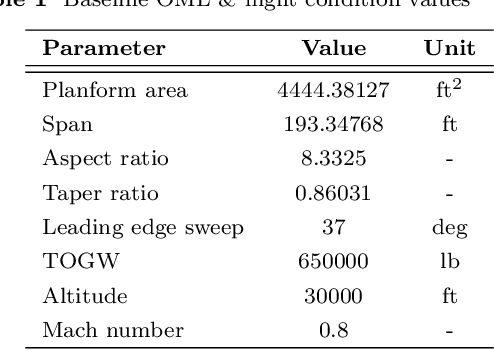
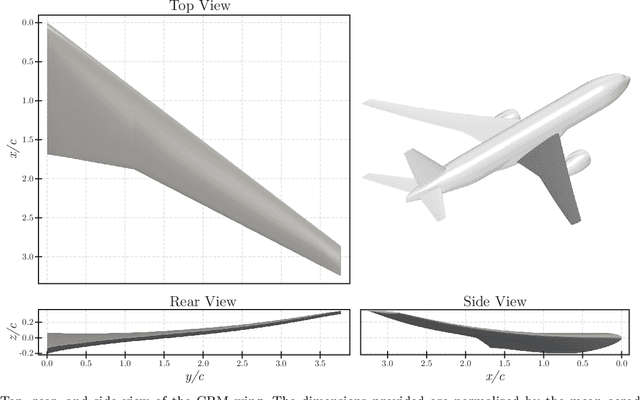
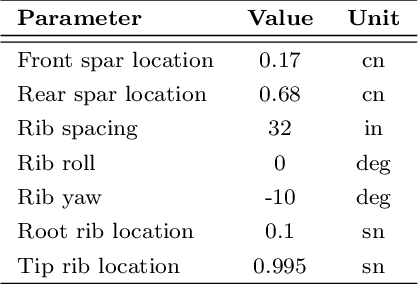
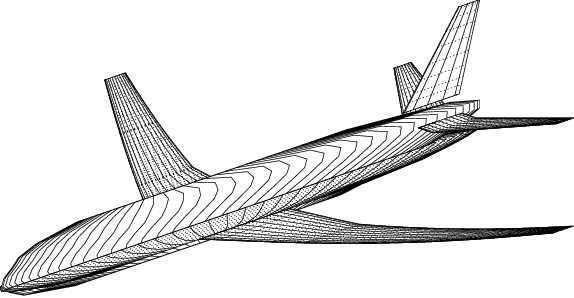
This work presents the application of a recently developed parametric, non-intrusive, and multi-fidelity reduced-order modeling method on high-dimensional displacement and stress fields arising from the structural analysis of geometries that differ in the size of discretization and structural topology.The proposed approach leverages manifold alignment to fuse inconsistent field outputs from high- and low-fidelity simulations by individually projecting their solution onto a common subspace. The effectiveness of the method is demonstrated on two multi-fidelity scenarios involving the structural analysis of a benchmark wing geometry. Results show that outputs from structural simulations using incompatible grids, or related yet different topologies, are easily combined into a single predictive model, thus eliminating the need for additional pre-processing of the data. The new multi-fidelity reduced-order model achieves a relatively higher predictive accuracy at a lower computational cost when compared to a single-fidelity model.