On the performance of multi-fidelity and reduced-dimensional neural emulators for inference of physiologic boundary conditions

Solving inverse problems in cardiovascular modeling is particularly challenging due to the high computational cost of running high-fidelity simulations. In this work, we focus on Bayesian parameter estimation and explore different methods to reduce the computational cost of sampling from the posterior distribution by leveraging low-fidelity approximations. A common approach is to construct a surrogate model for the high-fidelity simulation itself. Another is to build a surrogate for the discrepancy between high- and low-fidelity models. This discrepancy, which is often easier to approximate, is modeled with either a fully connected neural network or a nonlinear dimensionality reduction technique that enables surrogate construction in a lower-dimensional space. A third possible approach is to treat the discrepancy between the high-fidelity and surrogate models as random noise and estimate its distribution using normalizing flows. This allows us to incorporate the approximation error into the Bayesian inverse problem by modifying the likelihood function. We validate five different methods which are variations of the above on analytical test cases by comparing them to posterior distributions derived solely from high-fidelity models, assessing both accuracy and computational cost. Finally, we demonstrate our approaches on two cardiovascular examples of increasing complexity: a lumped-parameter Windkessel model and a patient-specific three-dimensional anatomy.

Enabling stratified sampling in high dimensions via nonlinear dimensionality reduction

We consider the problem of propagating the uncertainty from a possibly large number of random inputs through a computationally expensive model. Stratified sampling is a well-known variance reduction strategy, but its application, thus far, has focused on models with a limited number of inputs due to the challenges of creating uniform partitions in high dimensions. To overcome these challenges, we perform stratification with respect to the uniform distribution defined over the unit interval, and then derive the corresponding strata in the original space using nonlinear dimensionality reduction. We show that our approach is effective in high dimensions and can be used to further reduce the variance of multifidelity Monte Carlo estimators.

InVAErt networks for amortized inference and identifiability analysis of lumped parameter hemodynamic models

Estimation of cardiovascular model parameters from electronic health records (EHR) poses a significant challenge primarily due to lack of identifiability. Structural non-identifiability arises when a manifold in the space of parameters is mapped to a common output, while practical non-identifiability can result due to limited data, model misspecification, or noise corruption. To address the resulting ill-posed inverse problem, optimization-based or Bayesian inference approaches typically use regularization, thereby limiting the possibility of discovering multiple solutions. In this study, we use inVAErt networks, a neural network-based, data-driven framework for enhanced digital twin analysis of stiff dynamical systems. We demonstrate the flexibility and effectiveness of inVAErt networks in the context of physiological inversion of a six-compartment lumped parameter hemodynamic model from synthetic data to real data with missing components.

Quantification of total uncertainty in the physics-informed reconstruction of CVSim-6 physiology

When predicting physical phenomena through simulation, quantification of the total uncertainty due to multiple sources is as crucial as making sure the underlying numerical model is accurate. Possible sources include irreducible aleatoric uncertainty due to noise in the data, epistemic uncertainty induced by insufficient data or inadequate parameterization, and model-form uncertainty related to the use of misspecified model equations. Physics-based regularization interacts in nontrivial ways with aleatoric, epistemic and model-form uncertainty and their combination, and a better understanding of this interaction is needed to improve the predictive performance of physics-informed digital twins that operate under real conditions. With a specific focus on biological and physiological models, this study investigates the decomposition of total uncertainty in the estimation of states and parameters of a differential system simulated with MC X-TFC, a new physics-informed approach for uncertainty quantification based on random projections and Monte-Carlo sampling. MC X-TFC is applied to a six-compartment stiff ODE system, the CVSim-6 model, developed in the context of human physiology. The system is analyzed by progressively removing data while estimating an increasing number of parameters and by investigating total uncertainty under model-form misspecification of non-linear resistance in the pulmonary compartment. In particular, we focus on the interaction between the formulation of the discrepancy term and quantification of model-form uncertainty, and show how additional physics can help in the estimation process. The method demonstrates robustness and efficiency in estimating unknown states and parameters, even with limited, sparse, and noisy data. It also offers great flexibility in integrating data with physics for improved estimation, even in cases of model misspecification.

NeurAM: nonlinear dimensionality reduction for uncertainty quantification through neural active manifolds

We present a new approach for nonlinear dimensionality reduction, specifically designed for computationally expensive mathematical models. We leverage autoencoders to discover a one-dimensional neural active manifold (NeurAM) capturing the model output variability, plus a simultaneously learnt surrogate model with inputs on this manifold. The proposed dimensionality reduction framework can then be applied to perform outer loop many-query tasks, like sensitivity analysis and uncertainty propagation. In particular, we prove, both theoretically under idealized conditions, and numerically in challenging test cases, how NeurAM can be used to obtain multifidelity sampling estimators with reduced variance by sampling the models on the discovered low-dimensional and shared manifold among models. Several numerical examples illustrate the main features of the proposed dimensionality reduction strategy, and highlight its advantages with respect to existing approaches in the literature.

A Probabilistic Neural Twin for Treatment Planning in Peripheral Pulmonary Artery Stenosis

The substantial computational cost of high-fidelity models in numerical hemodynamics has, so far, relegated their use mainly to offline treatment planning. New breakthroughs in data-driven architectures and optimization techniques for fast surrogate modeling provide an exciting opportunity to overcome these limitations, enabling the use of such technology for time-critical decisions. We discuss an application to the repair of multiple stenosis in peripheral pulmonary artery disease through either transcatheter pulmonary artery rehabilitation or surgery, where it is of interest to achieve desired pressures and flows at specific locations in the pulmonary artery tree, while minimizing the risk for the patient. Since different degrees of success can be achieved in practice during treatment, we formulate the problem in probability, and solve it through a sample-based approach. We propose a new offline-online pipeline for probabilsitic real-time treatment planning which combines offline assimilation of boundary conditions, model reduction, and training dataset generation with online estimation of marginal probabilities, possibly conditioned on the degree of augmentation observed in already repaired lesions. Moreover, we propose a new approach for the parametrization of arbitrarily shaped vascular repairs through iterative corrections of a zero-dimensional approximant. We demonstrate this pipeline for a diseased model of the pulmonary artery tree available through the Vascular Model Repository.

InVAErt networks: a data-driven framework for emulation, inference and identifiability analysis

Use of generative models and deep learning for physics-based systems is currently dominated by the task of emulation. However, the remarkable flexibility offered by data-driven architectures would suggest to extend this representation to other aspects of system synthesis including model inversion and identifiability. We introduce inVAErt (pronounced \emph{invert}) networks, a comprehensive framework for data-driven analysis and synthesis of parametric physical systems which uses a deterministic encoder and decoder to represent the forward and inverse solution maps, normalizing flow to capture the probabilistic distribution of system outputs, and a variational encoder designed to learn a compact latent representation for the lack of bijectivity between inputs and outputs. We formally investigate the selection of penalty coefficients in the loss function and strategies for latent space sampling, since we find that these significantly affect both training and testing performance. We validate our framework through extensive numerical examples, including simple linear, nonlinear, and periodic maps, dynamical systems, and spatio-temporal PDEs.

LINFA: a Python library for variational inference with normalizing flow and annealing

Variational inference is an increasingly popular method in statistics and machine learning for approximating probability distributions. We developed LINFA (Library for Inference with Normalizing Flow and Annealing), a Python library for variational inference to accommodate computationally expensive models and difficult-to-sample distributions with dependent parameters. We discuss the theoretical background, capabilities, and performance of LINFA in various benchmarks. LINFA is publicly available on GitHub at https://github.com/desResLab/LINFA.

Differentially Private Normalizing Flows for Density Estimation, Data Synthesis, and Variational Inference with Application to Electronic Health Records

Electronic health records (EHR) often contain sensitive medical information about individual patients, posing significant limitations to sharing or releasing EHR data for downstream learning and inferential tasks. We use normalizing flows (NF), a family of deep generative models, to estimate the probability density of a dataset with differential privacy (DP) guarantees, from which privacy-preserving synthetic data are generated. We apply the technique to an EHR dataset containing patients with pulmonary hypertension. We assess the learning and inferential utility of the synthetic data by comparing the accuracy in the prediction of the hypertension status and variational posterior distribution of the parameters of a physics-based model. In addition, we use a simulated dataset from a nonlinear model to compare the results from variational inference (VI) based on privacy-preserving synthetic data, and privacy-preserving VI obtained from directly privatizing NFs for VI with DP guarantees given the original non-private dataset. The results suggest that synthetic data generated through differentially private density estimation with NF can yield good utility at a reasonable privacy cost. We also show that VI obtained from differentially private NF based on the free energy bound loss may produce variational approximations with significantly altered correlation structure, and loss formulations based on alternative dissimilarity metrics between two distributions might provide improved results.

Data-driven synchronization-avoiding algorithms in the explicit distributed structural analysis of soft tissue

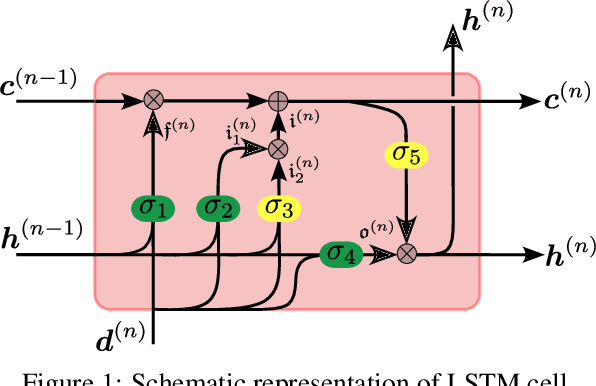
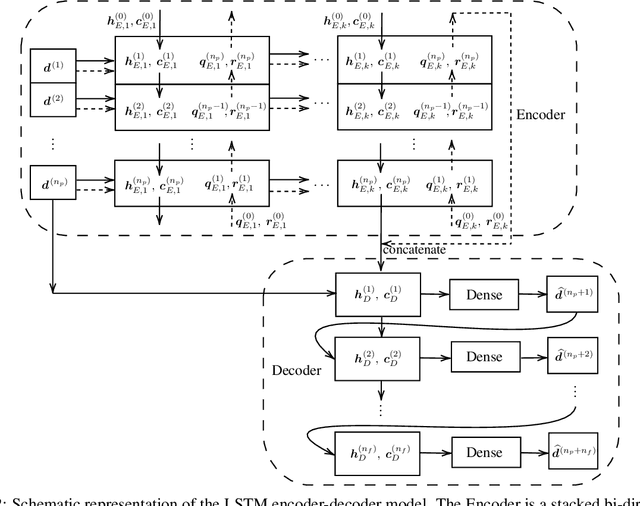
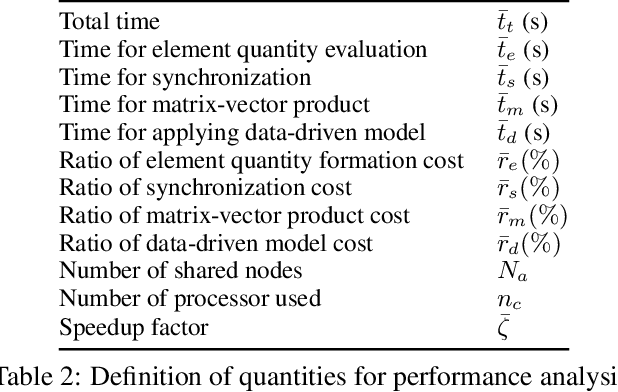
We propose a data-driven framework to increase the computational efficiency of the explicit finite element method in the structural analysis of soft tissue. An encoder-decoder long short-term memory deep neural network is trained based on the data produced by an explicit, distributed finite element solver. We leverage this network to predict synchronized displacements at shared nodes, minimizing the amount of communication between processors. We perform extensive numerical experiments to quantify the accuracy and stability of the proposed synchronization-avoiding algorithm.