Penzai + Treescope: A Toolkit for Interpreting, Visualizing, and Editing Models As Data

Much of today's machine learning research involves interpreting, modifying or visualizing models after they are trained. I present Penzai, a neural network library designed to simplify model manipulation by representing models as simple data structures, and Treescope, an interactive pretty-printer and array visualizer that can visualize both model inputs/outputs and the models themselves. Penzai models are built using declarative combinators that expose the model forward pass in the structure of the model object itself, and use named axes to ensure each operation is semantically meaningful. With Penzai's tree-editing selector system, users can both insert and replace model components, allowing them to intervene on intermediate values or make other edits to the model structure. Users can then get immediate feedback by visualizing the modified model with Treescope. I describe the motivation and main features of Penzai and Treescope, and discuss how treating the model as data enables a variety of analyses and interventions to be implemented as data-structure transformations, without requiring model designers to add explicit hooks.

Experts Don't Cheat: Learning What You Don't Know By Predicting Pairs

Identifying how much a model ${\widehat{p}}_{\theta}(Y|X)$ knows about the stochastic real-world process $p(Y|X)$ it was trained on is important to ensure it avoids producing incorrect or "hallucinated" answers or taking unsafe actions. But this is difficult for generative models because probabilistic predictions do not distinguish between per-response noise (aleatoric uncertainty) and lack of knowledge about the process (epistemic uncertainty), and existing epistemic uncertainty quantification techniques tend to be overconfident when the model underfits. We propose a general strategy for teaching a model to both approximate $p(Y|X)$ and also estimate the remaining gaps between ${\widehat{p}}_{\theta}(Y|X)$ and $p(Y|X)$: train it to predict pairs of independent responses drawn from the true conditional distribution, allow it to "cheat" by observing one response while predicting the other, then measure how much it cheats. Remarkably, we prove that being good at cheating (i.e. cheating whenever it improves your prediction) is equivalent to being second-order calibrated, a principled extension of ordinary calibration that allows us to construct provably-correct frequentist confidence intervals for $p(Y|X)$ and detect incorrect responses with high probability. We demonstrate empirically that our approach accurately estimates how much models don't know across ambiguous image classification, (synthetic) language modeling, and partially-observable navigation tasks, outperforming existing techniques.

A density estimation perspective on learning from pairwise human preferences

Learning from human feedback (LHF) -- and in particular learning from pairwise preferences -- has recently become a crucial ingredient in training large language models (LLMs), and has been the subject of much research. Most recent works frame it as a reinforcement learning problem, where a reward function is learned from pairwise preference data and the LLM is treated as a policy which is adapted to maximize the rewards, often under additional regularization constraints. We propose an alternative interpretation which centers on the generative process for pairwise preferences and treats LHF as a density estimation problem. We provide theoretical and empirical results showing that for a family of generative processes defined via preference behavior distribution equations, training a reward function on pairwise preferences effectively models an annotator's implicit preference distribution. Finally, we discuss and present findings on "annotator misspecification" -- failure cases where wrong modeling assumptions are made about annotator behavior, resulting in poorly-adapted models -- suggesting that approaches that learn from pairwise human preferences could have trouble learning from a population of annotators with diverse viewpoints.

R-U-SURE? Uncertainty-Aware Code Suggestions By Maximizing Utility Across Random User Intents

Large language models show impressive results at predicting structured text such as code, but also commonly introduce errors and hallucinations in their output. When used to assist software developers, these models may make mistakes that users must go back and fix, or worse, introduce subtle bugs that users may miss entirely. We propose Randomized Utility-driven Synthesis of Uncertain REgions (R-U-SURE), an approach for building uncertainty-aware suggestions based on a decision-theoretic model of goal-conditioned utility, using random samples from a generative model as a proxy for the unobserved possible intents of the end user. Our technique combines minimum-Bayes-risk decoding, dual decomposition, and decision diagrams in order to efficiently produce structured uncertainty summaries, given only sample access to an arbitrary generative model of code and an optional AST parser. We demonstrate R-U-SURE on three developer-assistance tasks, and show that it can be applied different user interaction patterns without retraining the model and leads to more accurate uncertainty estimates than token-probability baselines.

Contrastive Learning Can Find An Optimal Basis For Approximately View-Invariant Functions

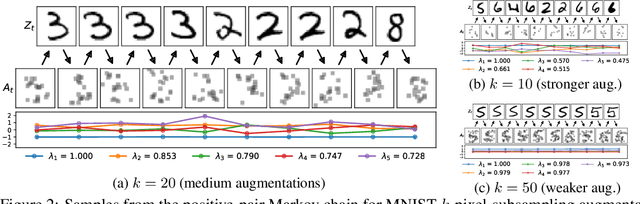
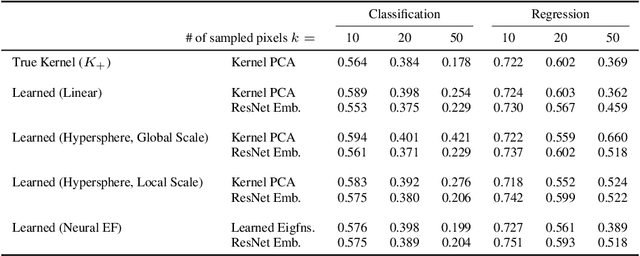
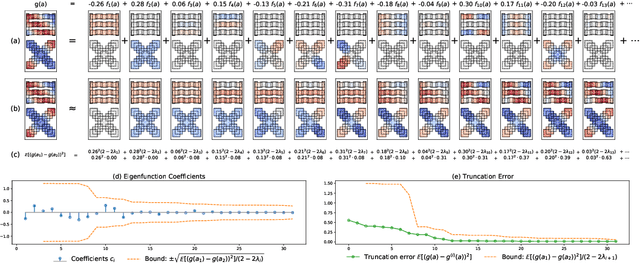
Contrastive learning is a powerful framework for learning self-supervised representations that generalize well to downstream supervised tasks. We show that multiple existing contrastive learning methods can be reinterpreted as learning kernel functions that approximate a fixed positive-pair kernel. We then prove that a simple representation obtained by combining this kernel with PCA provably minimizes the worst-case approximation error of linear predictors, under a straightforward assumption that positive pairs have similar labels. Our analysis is based on a decomposition of the target function in terms of the eigenfunctions of a positive-pair Markov chain, and a surprising equivalence between these eigenfunctions and the output of Kernel PCA. We give generalization bounds for downstream linear prediction using our Kernel PCA representation, and show empirically on a set of synthetic tasks that applying Kernel PCA to contrastive learning models can indeed approximately recover the Markov chain eigenfunctions, although the accuracy depends on the kernel parameterization as well as on the augmentation strength.

Learning Generalized Gumbel-max Causal Mechanisms

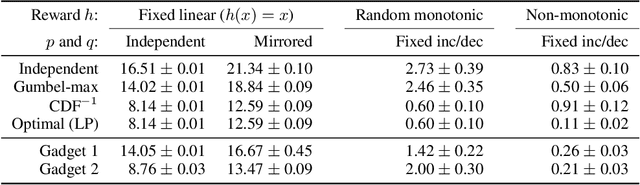
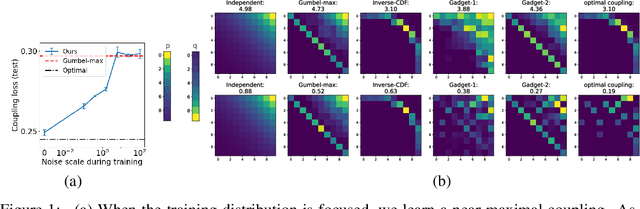
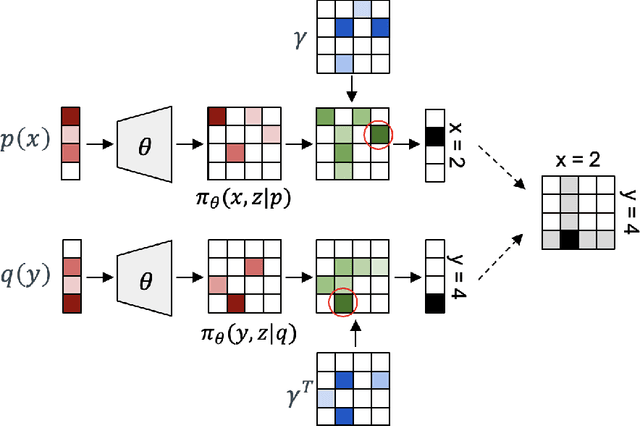
To perform counterfactual reasoning in Structural Causal Models (SCMs), one needs to know the causal mechanisms, which provide factorizations of conditional distributions into noise sources and deterministic functions mapping realizations of noise to samples. Unfortunately, the causal mechanism is not uniquely identified by data that can be gathered by observing and interacting with the world, so there remains the question of how to choose causal mechanisms. In recent work, Oberst & Sontag (2019) propose Gumbel-max SCMs, which use Gumbel-max reparameterizations as the causal mechanism due to an intuitively appealing counterfactual stability property. In this work, we instead argue for choosing a causal mechanism that is best under a quantitative criteria such as minimizing variance when estimating counterfactual treatment effects. We propose a parameterized family of causal mechanisms that generalize Gumbel-max. We show that they can be trained to minimize counterfactual effect variance and other losses on a distribution of queries of interest, yielding lower variance estimates of counterfactual treatment effect than fixed alternatives, also generalizing to queries not seen at training time.

Beyond In-Place Corruption: Insertion and Deletion In Denoising Probabilistic Models

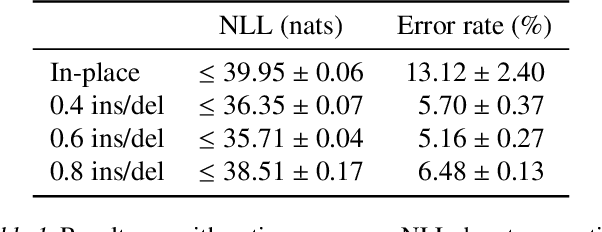
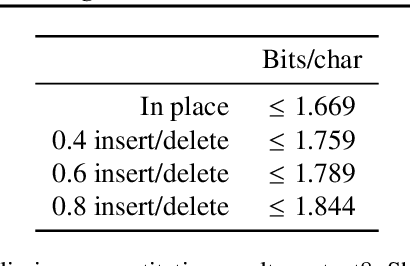
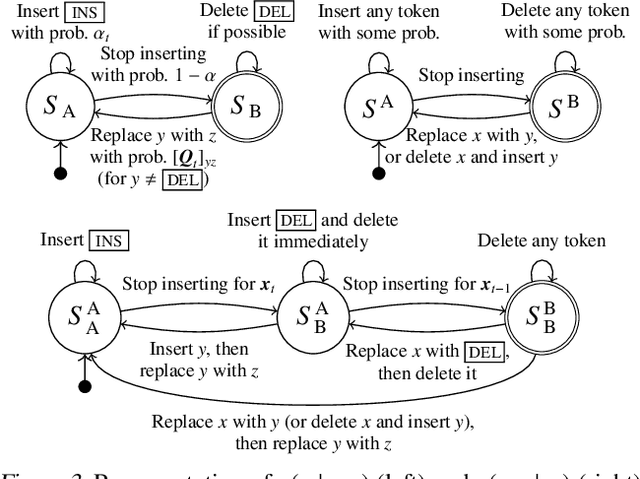
Denoising diffusion probabilistic models (DDPMs) have shown impressive results on sequence generation by iteratively corrupting each example and then learning to map corrupted versions back to the original. However, previous work has largely focused on in-place corruption, adding noise to each pixel or token individually while keeping their locations the same. In this work, we consider a broader class of corruption processes and denoising models over sequence data that can insert and delete elements, while still being efficient to train and sample from. We demonstrate that these models outperform standard in-place models on an arithmetic sequence task, and that when trained on the text8 dataset they can be used to fix spelling errors without any fine-tuning.

Structured Denoising Diffusion Models in Discrete State-Spaces

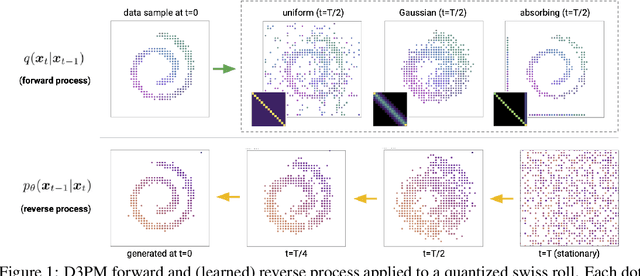
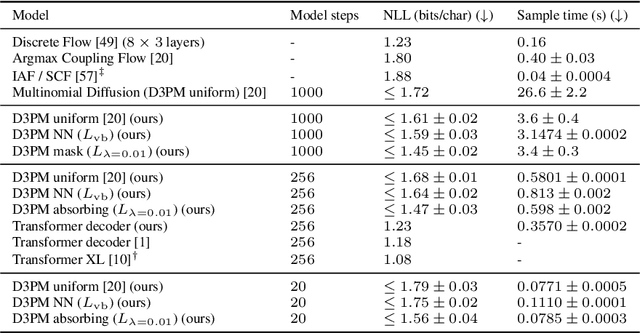
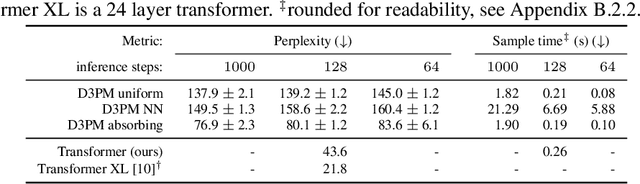
Denoising diffusion probabilistic models (DDPMs) (Ho et al. 2020) have shown impressive results on image and waveform generation in continuous state spaces. Here, we introduce Discrete Denoising Diffusion Probabilistic Models (D3PMs), diffusion-like generative models for discrete data that generalize the multinomial diffusion model of Hoogeboom et al. 2021, by going beyond corruption processes with uniform transition probabilities. This includes corruption with transition matrices that mimic Gaussian kernels in continuous space, matrices based on nearest neighbors in embedding space, and matrices that introduce absorbing states. The third allows us to draw a connection between diffusion models and autoregressive and mask-based generative models. We show that the choice of transition matrix is an important design decision that leads to improved results in image and text domains. We also introduce a new loss function that combines the variational lower bound with an auxiliary cross entropy loss. For text, this model class achieves strong results on character-level text generation while scaling to large vocabularies on LM1B. On the image dataset CIFAR-10, our models approach the sample quality and exceed the log-likelihood of the continuous-space DDPM model.

Learning Graph Structure With A Finite-State Automaton Layer

Graph-based neural network models are producing strong results in a number of domains, in part because graphs provide flexibility to encode domain knowledge in the form of relational structure (edges) between nodes in the graph. In practice, edges are used both to represent intrinsic structure (e.g., abstract syntax trees of programs) and more abstract relations that aid reasoning for a downstream task (e.g., results of relevant program analyses). In this work, we study the problem of learning to derive abstract relations from the intrinsic graph structure. Motivated by their power in program analyses, we consider relations defined by paths on the base graph accepted by a finite-state automaton. We show how to learn these relations end-to-end by relaxing the problem into learning finite-state automata policies on a graph-based POMDP and then training these policies using implicit differentiation. The result is a differentiable Graph Finite-State Automaton (GFSA) layer that adds a new edge type (expressed as a weighted adjacency matrix) to a base graph. We demonstrate that this layer can find shortcuts in grid-world graphs and reproduce simple static analyses on Python programs. Additionally, we combine the GFSA layer with a larger graph-based model trained end-to-end on the variable misuse program understanding task, and find that using the GFSA layer leads to better performance than using hand-engineered semantic edges or other baseline methods for adding learned edge types.