DOPPLER: Dual-Policy Learning for Device Assignment in Asynchronous Dataflow Graphs

We study the problem of assigning operations in a dataflow graph to devices to minimize execution time in a work-conserving system, with emphasis on complex machine learning workloads. Prior learning-based methods often struggle due to three key limitations: (1) reliance on bulk-synchronous systems like TensorFlow, which under-utilize devices due to barrier synchronization; (2) lack of awareness of the scheduling mechanism of underlying systems when designing learning-based methods; and (3) exclusive dependence on reinforcement learning, ignoring the structure of effective heuristics designed by experts. In this paper, we propose \textsc{Doppler}, a three-stage framework for training dual-policy networks consisting of 1) a $\mathsf{SEL}$ policy for selecting operations and 2) a $\mathsf{PLC}$ policy for placing chosen operations on devices. Our experiments show that \textsc{Doppler} outperforms all baseline methods across tasks by reducing system execution time and additionally demonstrates sampling efficiency by reducing per-episode training time.

Auto-Differentiation of Relational Computations for Very Large Scale Machine Learning

The relational data model was designed to facilitate large-scale data management and analytics. We consider the problem of how to differentiate computations expressed relationally. We show experimentally that a relational engine running an auto-differentiated relational algorithm can easily scale to very large datasets, and is competitive with state-of-the-art, special-purpose systems for large-scale distributed machine learning.

Tensor Relational Algebra for Machine Learning System Design

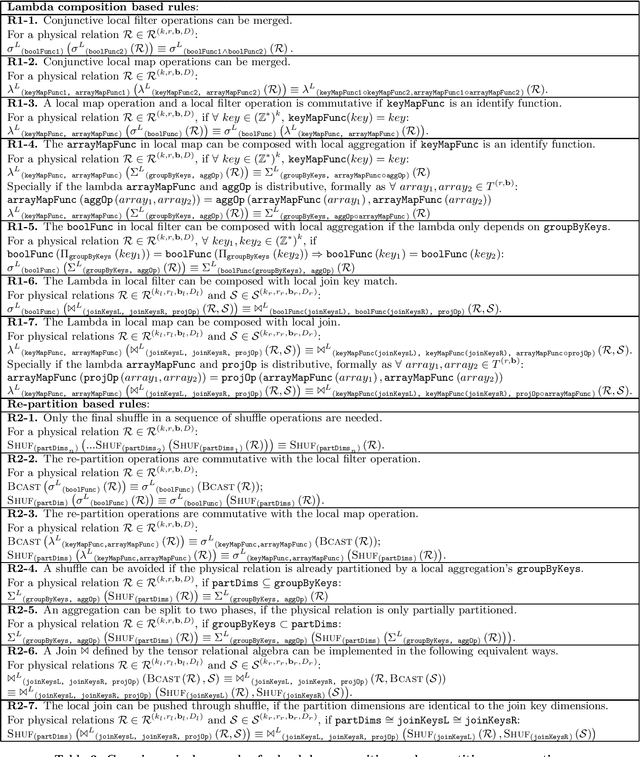
Machine learning (ML) systems have to support various tensor operations. However, such ML systems were largely developed without asking: what are the foundational abstractions necessary for building machine learning systems? We believe that proper computational and implementation abstractions will allow for the construction of self-configuring, declarative ML systems, especially when the goal is to execute tensor operations in a distributed environment, or partitioned across multiple AI accelerators (ASICs). To this end, we first introduce a tensor relational algebra (TRA), which is expressive to encode any tensor operation that can be written in the Einstein notation. We consider how TRA expressions can be re-written into an implementation algebra (IA) that enables effective implementation in a distributed environment, as well as how expressions in the IA can be optimized. Our empirical study shows that the optimized implementation provided by IA can reach or even out-perform carefully engineered HPC or ML systems for large scale tensor manipulations and ML workflows in distributed clusters.