Graph-Eq: Discovering Mathematical Equations using Graph Generative Models

The ability to discover meaningful, accurate, and concise mathematical equations that describe datasets is valuable across various domains. Equations offer explicit relationships between variables, enabling deeper insights into underlying data patterns. Most existing equation discovery methods rely on genetic programming, which iteratively searches the equation space but is often slow and prone to overfitting. By representing equations as directed acyclic graphs, we leverage the use of graph neural networks to learn the underlying semantics of equations, and generate new, previously unseen equations. Although graph generative models have been shown to be successful in discovering new types of graphs in many fields, there application in discovering equations remains largely unexplored. In this work, we propose Graph-EQ, a deep graph generative model designed for efficient equation discovery. Graph-EQ uses a conditional variational autoencoder (CVAE) to learn a rich latent representation of the equation space by training it on a large corpus of equations in an unsupervised manner. Instead of directly searching the equation space, we employ Bayesian optimization to efficiently explore this learned latent space. We show that the encoder-decoder architecture of Graph-Eq is able to accurately reconstruct input equations. Moreover, we show that the learned latent representation can be sampled and decoded into valid equations, including new and previously unseen equations in the training data. Finally, we assess Graph-Eq's ability to discover equations that best fit a dataset by exploring the latent space using Bayesian optimization. Latent space exploration is done on 20 dataset with known ground-truth equations, and Graph-Eq is shown to successfully discover the grountruth equation in the majority of datasets.

Arch-LLM: Taming LLMs for Neural Architecture Generation via Unsupervised Discrete Representation Learning

Unsupervised representation learning has been widely explored across various modalities, including neural architectures, where it plays a key role in downstream applications like Neural Architecture Search (NAS). These methods typically learn an unsupervised representation space before generating/ sampling architectures for the downstream search. A common approach involves the use of Variational Autoencoders (VAEs) to map discrete architectures onto a continuous representation space, however, sampling from these spaces often leads to a high percentage of invalid or duplicate neural architectures. This could be due to the unnatural mapping of inherently discrete architectural space onto a continuous space, which emphasizes the need for a robust discrete representation of these architectures. To address this, we introduce a Vector Quantized Variational Autoencoder (VQ-VAE) to learn a discrete latent space more naturally aligned with the discrete neural architectures. In contrast to VAEs, VQ-VAEs (i) map each architecture into a discrete code sequence and (ii) allow the prior to be learned by any generative model rather than assuming a normal distribution. We then represent these architecture latent codes as numerical sequences and train a text-to-text model leveraging a Large Language Model to learn and generate sequences representing architectures. We experiment our method with Inception/ ResNet-like cell-based search spaces, namely NAS-Bench-101 and NAS-Bench-201. Compared to VAE-based methods, our approach improves the generation of valid and unique architectures by over 80% on NASBench-101 and over 8% on NASBench-201. Finally, we demonstrate the applicability of our method in NAS employing a sequence-modeling-based NAS algorithm.

Day-ahead regional solar power forecasting with hierarchical temporal convolutional neural networks using historical power generation and weather data

Regional solar power forecasting, which involves predicting the total power generation from all rooftop photovoltaic systems in a region holds significant importance for various stakeholders in the energy sector. However, the vast amount of solar power generation and weather time series from geographically dispersed locations that need to be considered in the forecasting process makes accurate regional forecasting challenging. Therefore, previous work has limited the focus to either forecasting a single time series (i.e., aggregated time series) which is the addition of all solar generation time series in a region, disregarding the location-specific weather effects or forecasting solar generation time series of each PV site (i.e., individual time series) independently using location-specific weather data, resulting in a large number of forecasting models. In this work, we propose two deep-learning-based regional forecasting methods that can effectively leverage both types of time series (aggregated and individual) with weather data in a region. We propose two hierarchical temporal convolutional neural network architectures (HTCNN) and two strategies to adapt HTCNNs for regional solar power forecasting. At first, we explore generating a regional forecast using a single HTCNN. Next, we divide the region into multiple sub-regions based on weather information and train separate HTCNNs for each sub-region; the forecasts of each sub-region are then added to generate a regional forecast. The proposed work is evaluated using a large dataset collected over a year from 101 locations across Western Australia to provide a day ahead forecast. We compare our approaches with well-known alternative methods and show that the sub-region HTCNN requires fewer individual networks and achieves a forecast skill score of 40.2% reducing a statistically significant error by 6.5% compared to the best counterpart.

When To Grow? A Fitting Risk-Aware Policy for Layer Growing in Deep Neural Networks

Neural growth is the process of growing a small neural network to a large network and has been utilized to accelerate the training of deep neural networks. One crucial aspect of neural growth is determining the optimal growth timing. However, few studies investigate this systematically. Our study reveals that neural growth inherently exhibits a regularization effect, whose intensity is influenced by the chosen policy for growth timing. While this regularization effect may mitigate the overfitting risk of the model, it may lead to a notable accuracy drop when the model underfits. Yet, current approaches have not addressed this issue due to their lack of consideration of the regularization effect from neural growth. Motivated by these findings, we propose an under/over fitting risk-aware growth timing policy, which automatically adjusts the growth timing informed by the level of potential under/overfitting risks to address both risks. Comprehensive experiments conducted using CIFAR-10/100 and ImageNet datasets show that the proposed policy achieves accuracy improvements of up to 1.3% in models prone to underfitting while achieving similar accuracies in models suffering from overfitting compared to the existing methods.

GINN-LP: A Growing Interpretable Neural Network for Discovering Multivariate Laurent Polynomial Equations

Traditional machine learning is generally treated as a black-box optimization problem and does not typically produce interpretable functions that connect inputs and outputs. However, the ability to discover such interpretable functions is desirable. In this work, we propose GINN-LP, an interpretable neural network to discover the form and coefficients of the underlying equation of a dataset, when the equation is assumed to take the form of a multivariate Laurent Polynomial. This is facilitated by a new type of interpretable neural network block, named the "power-term approximator block", consisting of logarithmic and exponential activation functions. GINN-LP is end-to-end differentiable, making it possible to use backpropagation for training. We propose a neural network growth strategy that will enable finding the suitable number of terms in the Laurent polynomial that represents the data, along with sparsity regularization to promote the discovery of concise equations. To the best of our knowledge, this is the first model that can discover arbitrary multivariate Laurent polynomial terms without any prior information on the order. Our approach is first evaluated on a subset of data used in SRBench, a benchmark for symbolic regression. We first show that GINN-LP outperforms the state-of-the-art symbolic regression methods on datasets generated using 48 real-world equations in the form of multivariate Laurent polynomials. Next, we propose an ensemble method that combines our method with a high-performing symbolic regression method, enabling us to discover non-Laurent polynomial equations. We achieve state-of-the-art results in equation discovery, showing an absolute improvement of 7.1% over the best contender, by applying this ensemble method to 113 datasets within SRBench with known ground-truth equations.

NAPA-VQ: Neighborhood Aware Prototype Augmentation with Vector Quantization for Continual Learning

Catastrophic forgetting; the loss of old knowledge upon acquiring new knowledge, is a pitfall faced by deep neural networks in real-world applications. Many prevailing solutions to this problem rely on storing exemplars (previously encountered data), which may not be feasible in applications with memory limitations or privacy constraints. Therefore, the recent focus has been on Non-Exemplar based Class Incremental Learning (NECIL) where a model incrementally learns about new classes without using any past exemplars. However, due to the lack of old data, NECIL methods struggle to discriminate between old and new classes causing their feature representations to overlap. We propose NAPA-VQ: Neighborhood Aware Prototype Augmentation with Vector Quantization, a framework that reduces this class overlap in NECIL. We draw inspiration from Neural Gas to learn the topological relationships in the feature space, identifying the neighboring classes that are most likely to get confused with each other. This neighborhood information is utilized to enforce strong separation between the neighboring classes as well as to generate old class representative prototypes that can better aid in obtaining a discriminative decision boundary between old and new classes. Our comprehensive experiments on CIFAR-100, TinyImageNet, and ImageNet-Subset demonstrate that NAPA-VQ outperforms the State-of-the-art NECIL methods by an average improvement of 5%, 2%, and 4% in accuracy and 10%, 3%, and 9% in forgetting respectively. Our code can be found in https://github.com/TamashaM/NAPA-VQ.git.

DALLE-URBAN: Capturing the urban design expertise of large text to image transformers

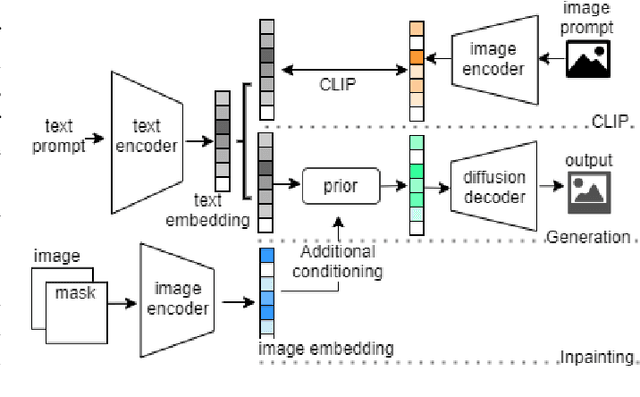
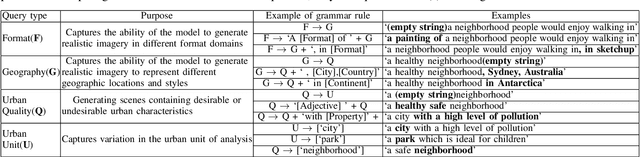
Automatically converting text descriptions into images using transformer architectures has recently received considerable attention. Such advances have implications for many applied design disciplines across fashion, art, architecture, urban planning, landscape design and the future tools available to such disciplines. However, a detailed analysis capturing the capabilities of such models, specifically with a focus on the built environment, has not been performed to date. In this work, we investigate the capabilities and biases of such text-to-image methods as it applies to the built environment in detail. We use a systematic grammar to generate queries related to the built environment and evaluate resulting generated images. We generate 1020 different images and find that text to image transformers are robust at generating realistic images across different domains for this use-case. Generated imagery can be found at the github: https://github.com/sachith500/DALLEURBAN

Self Organizing Nebulous Growths for Robust and Incremental Data Visualization

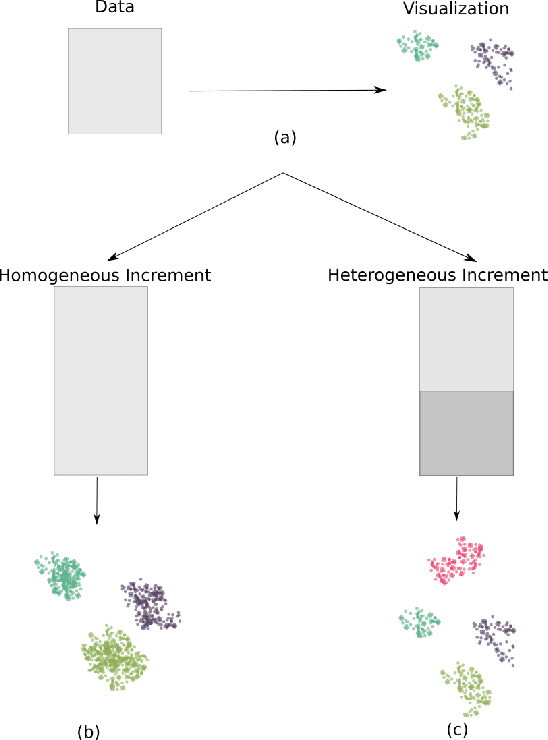
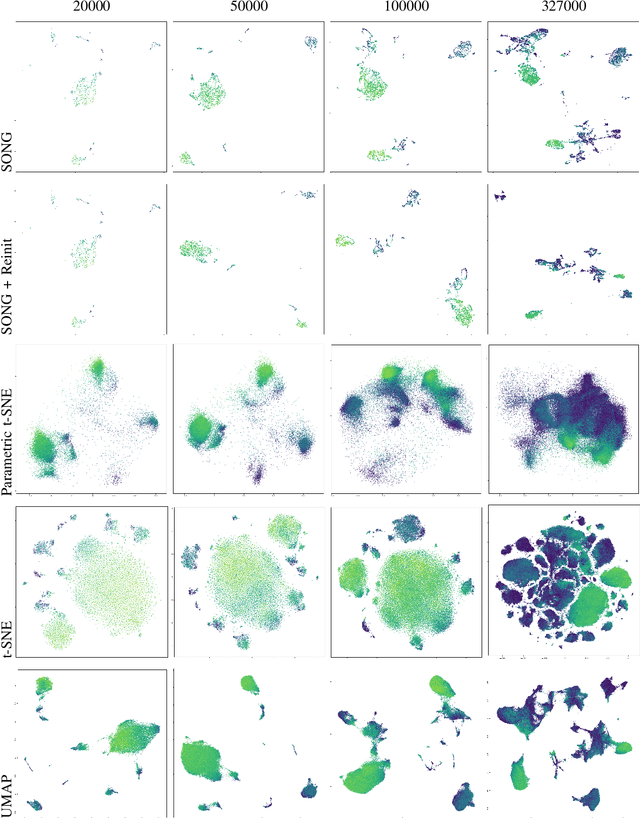
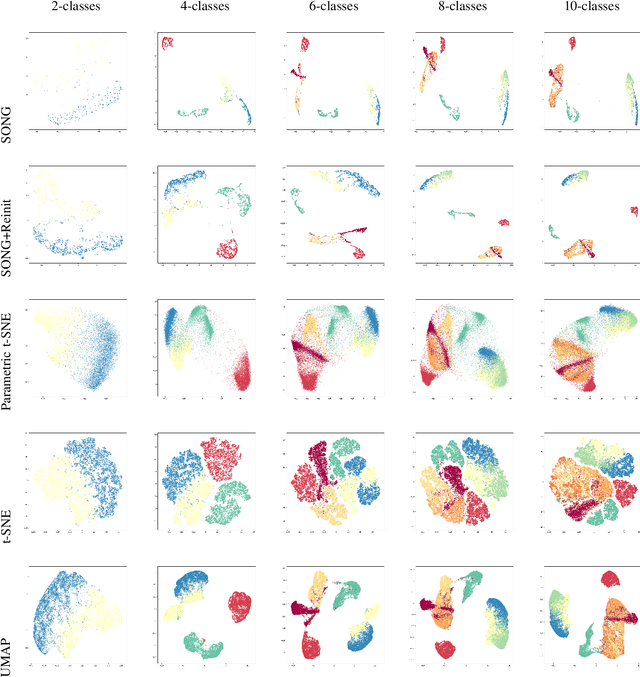
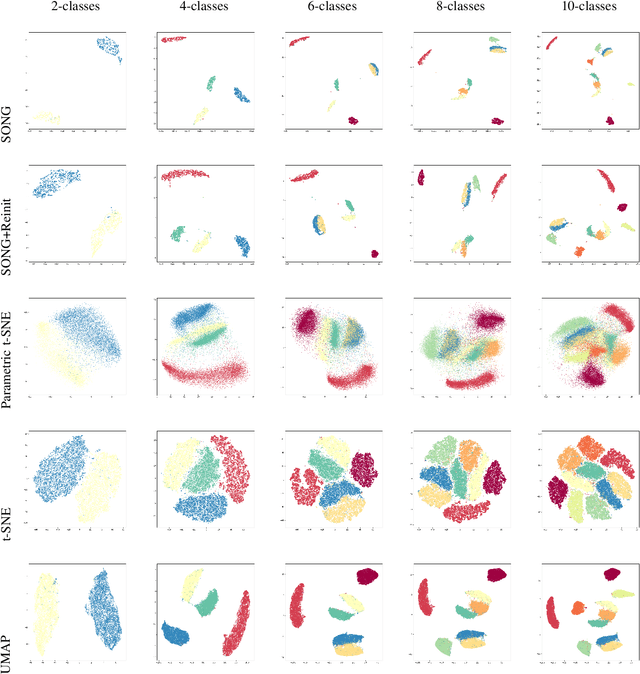
Non-parametric dimensionality reduction techniques, such as t-SNE and UMAP, are proficient in providing visualizations for fixed or static datasets, but they cannot incrementally map and insert new data points into existing data visualizations. We present Self-Organizing Nebulous Growths (SONG), a parametric nonlinear dimensionality reduction technique that supports incremental data visualization, i.e., incremental addition of new data while preserving the structure of the existing visualization. In addition, SONG is capable of handling new data increments no matter whether they are similar or heterogeneous to the existing observations in distribution. We test SONG on a variety of real and simulated datasets. The results show that SONG is superior to Parametric t-SNE, t-SNE and UMAP in incremental data visualization. Specifically, for heterogeneous increments, SONG improves over Parametric t-SNE by 14.98 % on the Fashion MNIST dataset and 49.73% on the MNIST dataset regarding the cluster quality measured by the Adjusted Mutual Information scores. On similar or homogeneous increments, the improvements are 8.36% and 42.26% respectively. Furthermore, even in static cases, SONG performs better or comparable to UMAP, and superior to t-SNE. We also demonstrate that the algorithmic foundations of SONG render it more tolerant to noise compared to UMAP and t-SNE, thus providing greater utility for data with high variance or high mixing of clusters or noise.