Meta-Optimization and Program Search using Language Models for Task and Motion Planning

Intelligent interaction with the real world requires robotic agents to jointly reason over high-level plans and low-level controls. Task and motion planning (TAMP) addresses this by combining symbolic planning and continuous trajectory generation. Recently, foundation model approaches to TAMP have presented impressive results, including fast planning times and the execution of natural language instructions. Yet, the optimal interface between high-level planning and low-level motion generation remains an open question: prior approaches are limited by either too much abstraction (e.g., chaining simplified skill primitives) or a lack thereof (e.g., direct joint angle prediction). Our method introduces a novel technique employing a form of meta-optimization to address these issues by: (i) using program search over trajectory optimization problems as an interface between a foundation model and robot control, and (ii) leveraging a zero-order method to optimize numerical parameters in the foundation model output. Results on challenging object manipulation and drawing tasks confirm that our proposed method improves over prior TAMP approaches.

Stein Variational Evolution Strategies

Stein Variational Gradient Descent (SVGD) is a highly efficient method to sample from an unnormalized probability distribution. However, the SVGD update relies on gradients of the log-density, which may not always be available. Existing gradient-free versions of SVGD make use of simple Monte Carlo approximations or gradients from surrogate distributions, both with limitations. To improve gradient-free Stein variational inference, we combine SVGD steps with evolution strategy (ES) updates. Our results demonstrate that the resulting algorithm generates high-quality samples from unnormalized target densities without requiring gradient information. Compared to prior gradient-free SVGD methods, we find that the integration of the ES update in SVGD significantly improves the performance on multiple challenging benchmark problems.

NLP Sampling: Combining MCMC and NLP Methods for Diverse Constrained Sampling

Generating diverse samples under hard constraints is a core challenge in many areas. With this work we aim to provide an integrative view and framework to combine methods from the fields of MCMC, constrained optimization, as well as robotics, and gain insights in their strengths from empirical evaluations. We propose NLP Sampling as a general problem formulation, propose a family of restarting two-phase methods as a framework to integrated methods from across the fields, and evaluate them on analytical and robotic manipulation planning problems. Complementary to this, we provide several conceptual discussions, e.g. on the role of Lagrange parameters, global sampling, and the idea of a Diffused NLP and a corresponding model-based denoising sampler.

RHH-LGP: Receding Horizon And Heuristics-Based Logic-Geometric Programming For Task And Motion Planning

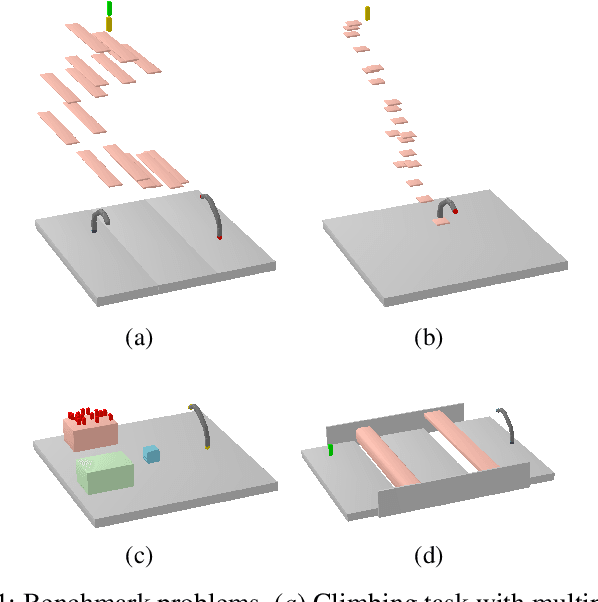
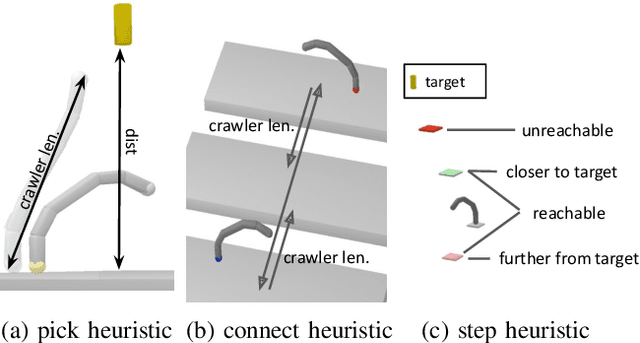
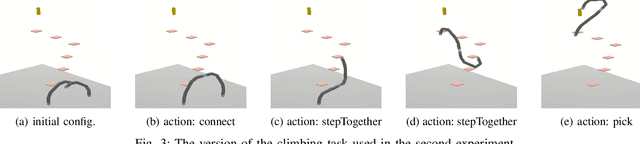
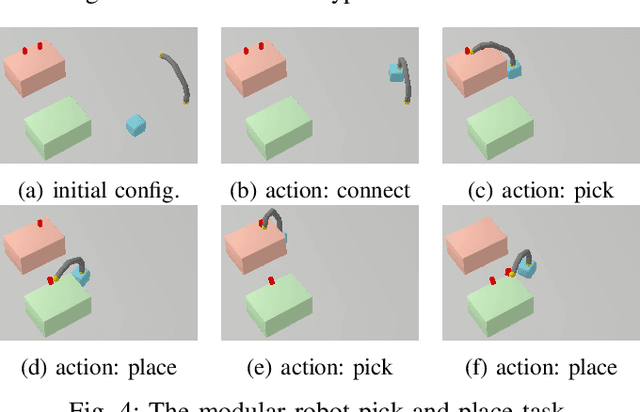
Sequential decision-making and motion planning for robotic manipulation induce combinatorial complexity. For long-horizon tasks, especially when the environment comprises many objects that can be interacted with, planning efficiency becomes even more important. To plan such long-horizon tasks, we present the RHH-LGP algorithm for combined task and motion planning (TAMP). First, we propose a TAMP approach (based on Logic-Geometric Programming) that effectively uses geometry-based heuristics for solving long-horizon manipulation tasks. We further improve the efficiency of this planner by a receding horizon formulation, resulting in RHH-LGP. We demonstrate the effectiveness and generality of our approach on several long-horizon tasks that require reasoning about interactions with a large number of objects. Using our framework, we can solve tasks that require multiple robots, including a mobile robot and snake-like walking robots, to form novel heterogeneous kinematic structures autonomously.