SoS1: O1 and R1-Like Reasoning LLMs are Sum-of-Square Solvers

Large Language Models (LLMs) have achieved human-level proficiency across diverse tasks, but their ability to perform rigorous mathematical problem solving remains an open challenge. In this work, we investigate a fundamental yet computationally intractable problem: determining whether a given multivariate polynomial is nonnegative. This problem, closely related to Hilbert's Seventeenth Problem, plays a crucial role in global polynomial optimization and has applications in various fields. First, we introduce SoS-1K, a meticulously curated dataset of approximately 1,000 polynomials, along with expert-designed reasoning instructions based on five progressively challenging criteria. Evaluating multiple state-of-the-art LLMs, we find that without structured guidance, all models perform only slightly above the random guess baseline 50%. However, high-quality reasoning instructions significantly improve accuracy, boosting performance up to 81%. Furthermore, our 7B model, SoS-7B, fine-tuned on SoS-1K for just 4 hours, outperforms the 671B DeepSeek-V3 and GPT-4o-mini in accuracy while only requiring 1.8% and 5% of the computation time needed for letters, respectively. Our findings highlight the potential of LLMs to push the boundaries of mathematical reasoning and tackle NP-hard problems.

Random Subspace Cubic-Regularization Methods, with Applications to Low-Rank Functions

We propose and analyze random subspace variants of the second-order Adaptive Regularization using Cubics (ARC) algorithm. These methods iteratively restrict the search space to some random subspace of the parameters, constructing and minimizing a local model only within this subspace. Thus, our variants only require access to (small-dimensional) projections of first- and second-order problem derivatives and calculate a reduced step inexpensively. Under suitable assumptions, the ensuing methods maintain the optimal first-order, and second-order, global rates of convergence of (full-dimensional) cubic regularization, while showing improved scalability both theoretically and numerically, particularly when applied to low-rank functions. When applied to the latter, our adaptive variant naturally adapts the subspace size to the true rank of the function, without knowing it a priori.

Dimensionality Reduction Techniques for Global Bayesian Optimisation

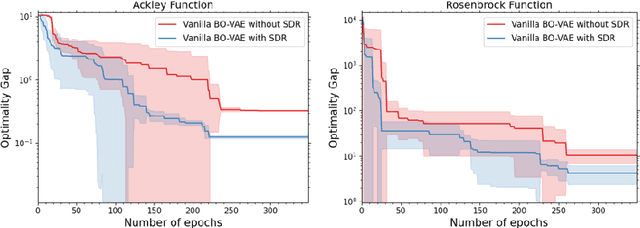
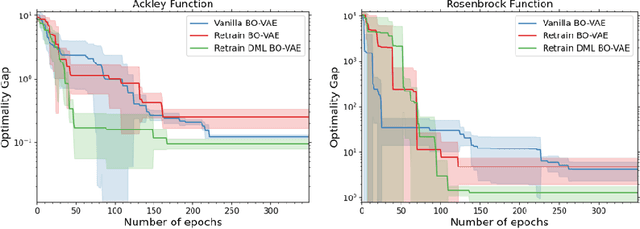
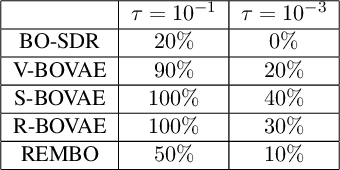
Bayesian Optimisation (BO) is a state-of-the-art global optimisation technique for black-box problems where derivative information is unavailable, and sample efficiency is crucial. However, improving the general scalability of BO has proved challenging. Here, we explore Latent Space Bayesian Optimisation (LSBO), that applies dimensionality reduction to perform BO in a reduced-dimensional subspace. While early LSBO methods used (linear) random projections (Wang et al., 2013), we employ Variational Autoencoders (VAEs) to manage more complex data structures and general DR tasks. Building on Grosnit et. al. (2021), we analyse the VAE-based LSBO framework, focusing on VAE retraining and deep metric loss. We suggest a few key corrections in their implementation, originally designed for tasks such as molecule generation, and reformulate the algorithm for broader optimisation purposes. Our numerical results show that structured latent manifolds improve BO performance. Additionally, we examine the use of the Mat\'{e}rn-$\frac{5}{2}$ kernel for Gaussian Processes in this LSBO context. We also integrate Sequential Domain Reduction (SDR), a standard global optimization efficiency strategy, into BO. SDR is included in a GPU-based environment using \textit{BoTorch}, both in the original and VAE-generated latent spaces, marking the first application of SDR within LSBO.

Registration of algebraic varieties using Riemannian optimization

We consider the point cloud registration problem, the task of finding a transformation between two point clouds that represent the same object but are expressed in different coordinate systems. Our approach is not based on a point-to-point correspondence, matching every point in the source point cloud to a point in the target point cloud. Instead, we assume and leverage a low-dimensional nonlinear geometric structure of the data. Firstly, we approximate each point cloud by an algebraic variety (a set defined by finitely many polynomial equations). This is done by solving an optimization problem on the Grassmann manifold, using a connection between algebraic varieties and polynomial bases. Secondly, we solve an optimization problem on the orthogonal group to find the transformation (rotation $+$ translation) which makes the two algebraic varieties overlap. We use second-order Riemannian optimization methods for the solution of both steps. Numerical experiments on real and synthetic data are provided, with encouraging results. Our approach is particularly useful when the two point clouds describe different parts of an objects (which may not even be overlapping), on the condition that the surface of the object may be well approximated by a set of polynomial equations. The first procedure -- the approximation -- is of independent interest, as it can be used for denoising data that belongs to an algebraic variety. We provide statistical guarantees for the estimation error of the denoising using Stein's unbiased estimator.

A Randomised Subspace Gauss-Newton Method for Nonlinear Least-Squares

We propose a Randomised Subspace Gauss-Newton (R-SGN) algorithm for solving nonlinear least-squares optimization problems, that uses a sketched Jacobian of the residual in the variable domain and solves a reduced linear least-squares on each iteration. A sublinear global rate of convergence result is presented for a trust-region variant of R-SGN, with high probability, which matches deterministic counterpart results in the order of the accuracy tolerance. Promising preliminary numerical results are presented for R-SGN on logistic regression and on nonlinear regression problems from the CUTEst collection.

Nonlinear matrix recovery using optimization on the Grassmann manifold

We investigate the problem of recovering a partially observed high-rank matrix whose columns obey a nonlinear structure such as a union of subspaces, an algebraic variety or grouped in clusters. The recovery problem is formulated as the rank minimization of a nonlinear feature map applied to the original matrix, which is then further approximated by a constrained non-convex optimization problem involving the Grassmann manifold. We propose two sets of algorithms, one arising from Riemannian optimization and the other as an alternating minimization scheme, both of which include first- and second-order variants. Both sets of algorithms have theoretical guarantees. In particular, for the alternating minimization, we establish global convergence and worst-case complexity bounds. Additionally, using the Kurdyka-Lojasiewicz property, we show that the alternating minimization converges to a unique limit point. We provide extensive numerical results for the recovery of union of subspaces and clustering under entry sampling and dense Gaussian sampling. Our methods are competitive with existing approaches and, in particular, high accuracy is achieved in the recovery using Riemannian second-order methods.

Global optimization using random embeddings

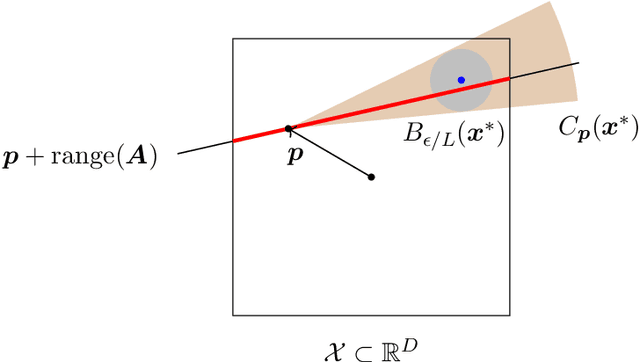
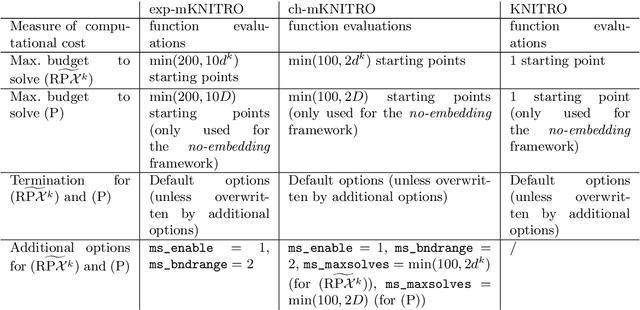
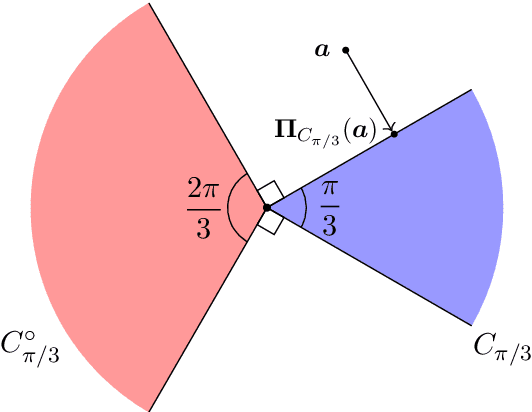
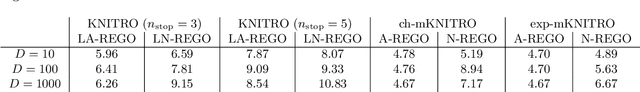
We propose a random-subspace algorithmic framework for global optimization of Lipschitz-continuous objectives, and analyse its convergence using novel tools from conic integral geometry. X-REGO randomly projects, in a sequential or simultaneous manner, the high-dimensional original problem into low-dimensional subproblems that can then be solved with any global, or even local, optimization solver. We estimate the probability that the randomly-embedded subproblem shares (approximately) the same global optimum as the original problem. This success probability is then used to show convergence of X-REGO to an approximate global solution of the original problem, under weak assumptions on the problem (having a strictly feasible global solution) and on the solver (guaranteed to find an approximate global solution of the reduced problem with sufficiently high probability). In the particular case of unconstrained objectives with low effective dimension, that only vary over a low-dimensional subspace, we propose an X-REGO variant that explores random subspaces of increasing dimension until finding the effective dimension of the problem, leading to X-REGO globally converging after a finite number of embeddings, proportional to the effective dimension. We show numerically that this variant efficiently finds both the effective dimension and an approximate global minimizer of the original problem.

Hashing embeddings of optimal dimension, with applications to linear least squares

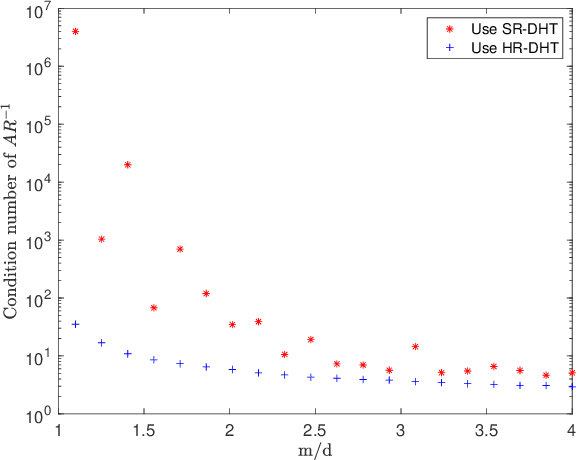
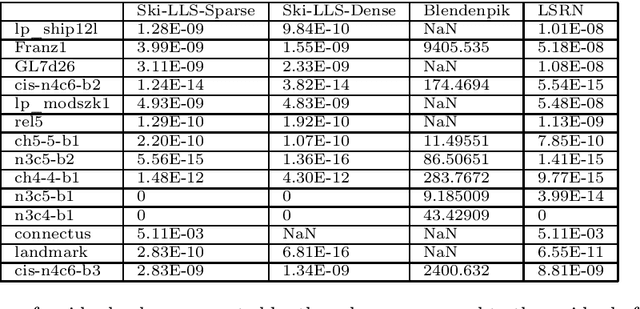
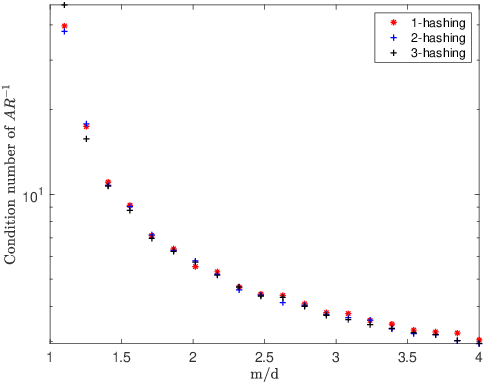
The aim of this paper is two-fold: firstly, to present subspace embedding properties for $s$-hashing sketching matrices, with $s\geq 1$, that are optimal in the projection dimension $m$ of the sketch, namely, $m=\mathcal{O}(d)$, where $d$ is the dimension of the subspace. A diverse set of results are presented that address the case when the input matrix has sufficiently low coherence (thus removing the $\log^2 d$ factor dependence in $m$, in the low-coherence result of Bourgain et al (2015) at the expense of a smaller coherence requirement); how this coherence changes with the number $s$ of column nonzeros (allowing a scaling of $\sqrt{s}$ of the coherence bound), or is reduced through suitable transformations (when considering hashed -- instead of subsampled -- coherence reducing transformations such as randomised Hadamard). Secondly, we apply these general hashing sketching results to the special case of Linear Least Squares (LLS), and develop Ski-LLS, a generic software package for these problems, that builds upon and improves the Blendenpik solver on dense input and the (sequential) LSRN performance on sparse problems. In addition to the hashing sketching improvements, we add suitable linear algebra tools for rank-deficient and for sparse problems that lead Ski-LLS to outperform not only sketching-based routines on randomly generated input, but also state of the art direct solver SPQR and iterative code HSL on certain subsets of the sparse Florida matrix collection; namely, on least squares problems that are significantly overdetermined, or moderately sparse, or difficult.

Scalable Derivative-Free Optimization for Nonlinear Least-Squares Problems

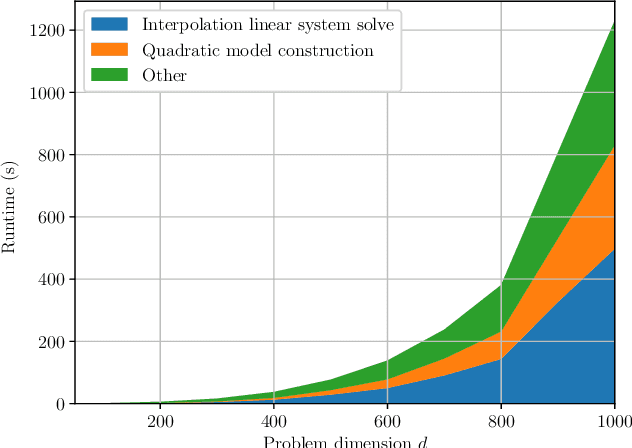
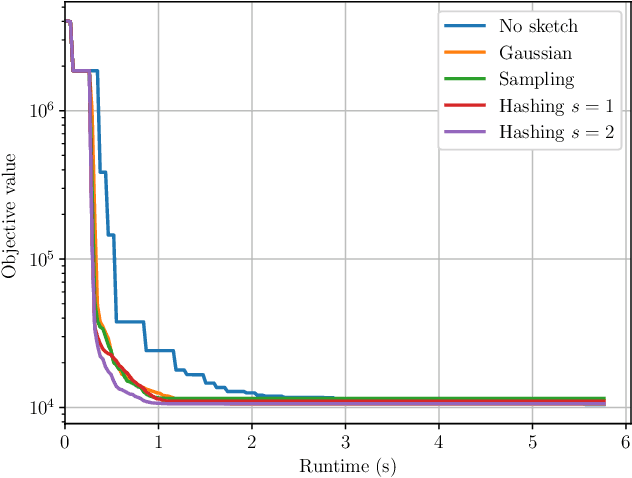
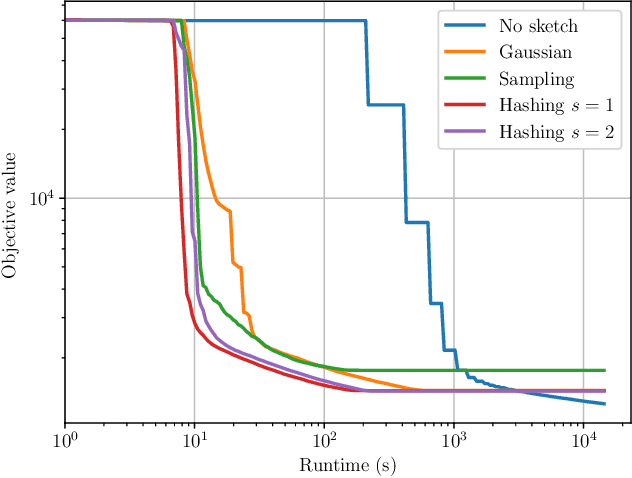
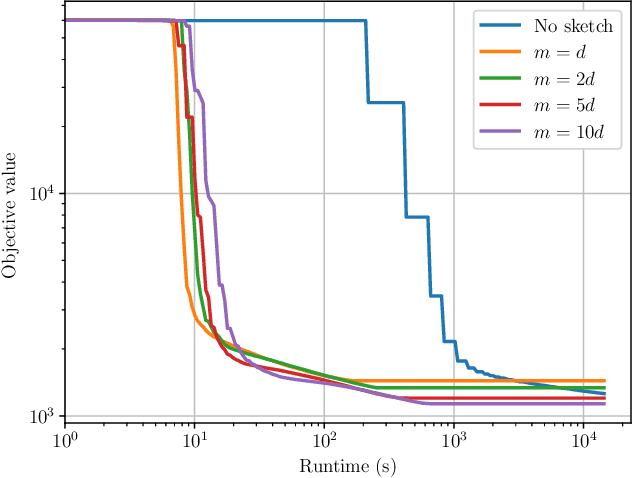
Derivative-free - or zeroth-order - optimization (DFO) has gained recent attention for its ability to solve problems in a variety of application areas, including machine learning, particularly involving objectives which are stochastic and/or expensive to compute. In this work, we develop a novel model-based DFO method for solving nonlinear least-squares problems. We improve on state-of-the-art DFO by performing dimensionality reduction in the observational space using sketching methods, avoiding the construction of a full local model. Our approach has a per-iteration computational cost which is linear in problem dimension in a big data regime, and numerical evidence demonstrates that, compared to existing software, it has dramatically improved runtime performance on overdetermined least-squares problems.

Sharp worst-case evaluation complexity bounds for arbitrary-order nonconvex optimization with inexpensive constraints

We provide sharp worst-case evaluation complexity bounds for nonconvex minimization problems with general inexpensive constraints, i.e.\ problems where the cost of evaluating/enforcing of the (possibly nonconvex or even disconnected) constraints, if any, is negligible compared to that of evaluating the objective function. These bounds unify, extend or improve all known upper and lower complexity bounds for unconstrained and convexly-constrained problems. It is shown that, given an accuracy level $\epsilon$, a degree of highest available Lipschitz continuous derivatives $p$ and a desired optimality order $q$ between one and $p$, a conceptual regularization algorithm requires no more than $O(\epsilon^{-\frac{p+1}{p-q+1}})$ evaluations of the objective function and its derivatives to compute a suitably approximate $q$-th order minimizer. With an appropriate choice of the regularization, a similar result also holds if the $p$-th derivative is merely H\"older rather than Lipschitz continuous. We provide an example that shows that the above complexity bound is sharp for unconstrained and a wide class of constrained problems, we also give reasons for the optimality of regularization methods from a worst-case complexity point of view, within a large class of algorithms that use the same derivative information.