Bilevel Learning with Inexact Stochastic Gradients

Bilevel learning has gained prominence in machine learning, inverse problems, and imaging applications, including hyperparameter optimization, learning data-adaptive regularizers, and optimizing forward operators. The large-scale nature of these problems has led to the development of inexact and computationally efficient methods. Existing adaptive methods predominantly rely on deterministic formulations, while stochastic approaches often adopt a doubly-stochastic framework with impractical variance assumptions, enforces a fixed number of lower-level iterations, and requires extensive tuning. In this work, we focus on bilevel learning with strongly convex lower-level problems and a nonconvex sum-of-functions in the upper-level. Stochasticity arises from data sampling in the upper-level which leads to inexact stochastic hypergradients. We establish their connection to state-of-the-art stochastic optimization theory for nonconvex objectives. Furthermore, we prove the convergence of inexact stochastic bilevel optimization under mild assumptions. Our empirical results highlight significant speed-ups and improved generalization in imaging tasks such as image denoising and deblurring in comparison with adaptive deterministic bilevel methods.

Non-Uniform Smoothness for Gradient Descent

The analysis of gradient descent-type methods typically relies on the Lipschitz continuity of the objective gradient. This generally requires an expensive hyperparameter tuning process to appropriately calibrate a stepsize for a given problem. In this work we introduce a local first-order smoothness oracle (LFSO) which generalizes the Lipschitz continuous gradients smoothness condition and is applicable to any twice-differentiable function. We show that this oracle can encode all relevant problem information for tuning stepsizes for a suitably modified gradient descent method and give global and local convergence results. We also show that LFSOs in this modified first-order method can yield global linear convergence rates for non-strongly convex problems with extremely flat minima, and thus improve over the lower bound on rates achievable by general (accelerated) first-order methods.

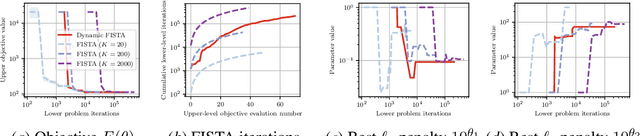
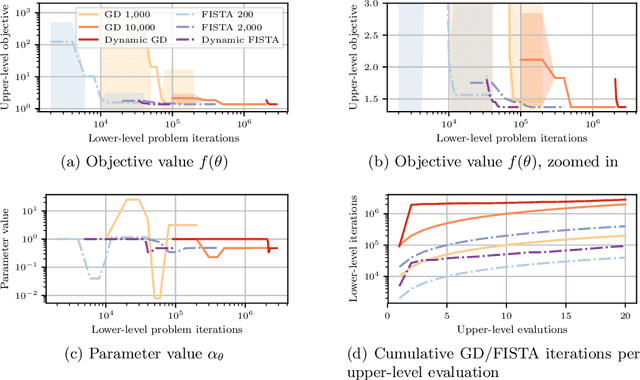
Dynamic Bilevel Learning with Inexact Line Search

In various domains within imaging and data science, particularly when addressing tasks modeled utilizing the variational regularization approach, manually configuring regularization parameters presents a formidable challenge. The difficulty intensifies when employing regularizers involving a large number of hyperparameters. To overcome this challenge, bilevel learning is employed to learn suitable hyperparameters. However, due to the use of numerical solvers, the exact gradient with respect to the hyperparameters is unattainable, necessitating the use of methods relying on approximate gradients. State-of-the-art inexact methods a priori select a decreasing summable sequence of the required accuracy and only assure convergence given a sufficiently small fixed step size. Despite this, challenges persist in determining the Lipschitz constant of the hypergradient and identifying an appropriate fixed step size. Conversely, computing exact function values is not feasible, impeding the use of line search. In this work, we introduce a provably convergent inexact backtracking line search involving inexact function evaluations and hypergradients. We show convergence to a stationary point of the loss with respect to hyperparameters. Additionally, we propose an algorithm to determine the required accuracy dynamically. Our numerical experiments demonstrate the efficiency and feasibility of our approach for hyperparameter estimation in variational regularization problems, alongside its robustness in terms of the initial accuracy and step size choices.

Analyzing Inexact Hypergradients for Bilevel Learning

Estimating hyperparameters has been a long-standing problem in machine learning. We consider the case where the task at hand is modeled as the solution to an optimization problem. Here the exact gradient with respect to the hyperparameters cannot be feasibly computed and approximate strategies are required. We introduce a unified framework for computing hypergradients that generalizes existing methods based on the implicit function theorem and automatic differentiation/backpropagation, showing that these two seemingly disparate approaches are actually tightly connected. Our framework is extremely flexible, allowing its subproblems to be solved with any suitable method, to any degree of accuracy. We derive a priori and computable a posteriori error bounds for all our methods, and numerically show that our a posteriori bounds are usually more accurate. Our numerical results also show that, surprisingly, for efficient bilevel optimization, the choice of hypergradient algorithm is at least as important as the choice of lower-level solver.

Optimizing illumination patterns for classical ghost imaging

Classical ghost imaging is a new paradigm in imaging where the image of an object is not measured directly with a pixelated detector. Rather, the object is subject to a set of illumination patterns and the total interaction of the object, e.g., reflected or transmitted photons or particles, is measured for each pattern with a single-pixel or bucket detector. An image of the object is then computed through the correlation of each pattern and the corresponding bucket value. Assuming no prior knowledge of the object, the set of patterns used to compute the ghost image dictates the image quality. In the visible-light regime, programmable spatial light modulators can generate the illumination patterns. In many other regimes -- such as x rays, electrons, and neutrons -- no such dynamically configurable modulators exist, and patterns are commonly produced by employing a transversely-translated mask. In this paper we explore some of the properties of masks or speckle that should be considered to maximize ghost-image quality, given a certain experimental classical ghost-imaging setup employing a transversely-displaced but otherwise non-configurable mask.

A simplified convergence theory for Byzantine resilient stochastic gradient descent

In distributed learning, a central server trains a model according to updates provided by nodes holding local data samples. In the presence of one or more malicious servers sending incorrect information (a Byzantine adversary), standard algorithms for model training such as stochastic gradient descent (SGD) fail to converge. In this paper, we present a simplified convergence theory for the generic Byzantine Resilient SGD method originally proposed by Blanchard et al. [NeurIPS 2017]. Compared to the existing analysis, we shown convergence to a stationary point in expectation under standard assumptions on the (possibly nonconvex) objective function and flexible assumptions on the stochastic gradients.

Efficient Hyperparameter Tuning with Dynamic Accuracy Derivative-Free Optimization

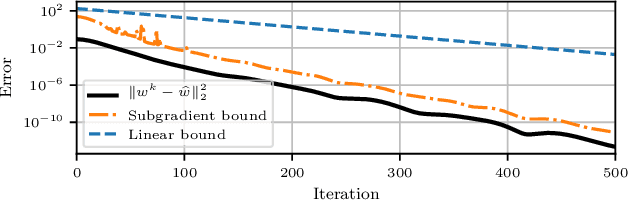
Many machine learning solutions are framed as optimization problems which rely on good hyperparameters. Algorithms for tuning these hyperparameters usually assume access to exact solutions to the underlying learning problem, which is typically not practical. Here, we apply a recent dynamic accuracy derivative-free optimization method to hyperparameter tuning, which allows inexact evaluations of the learning problem while retaining convergence guarantees. We test the method on the problem of learning elastic net weights for a logistic classifier, and demonstrate its robustness and efficiency compared to a fixed accuracy approach. This demonstrates a promising approach for hyperparameter tuning, with both convergence guarantees and practical performance.

Scalable Derivative-Free Optimization for Nonlinear Least-Squares Problems

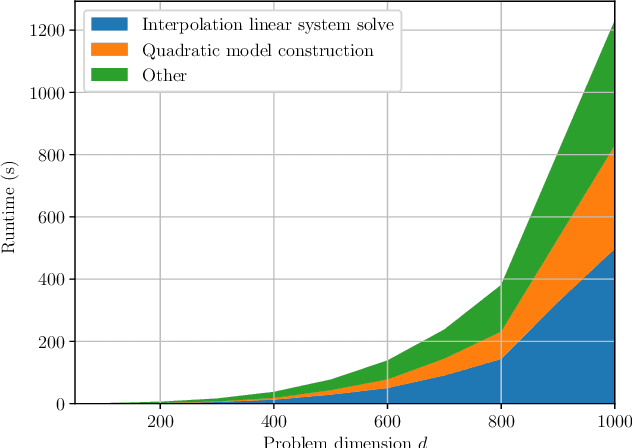
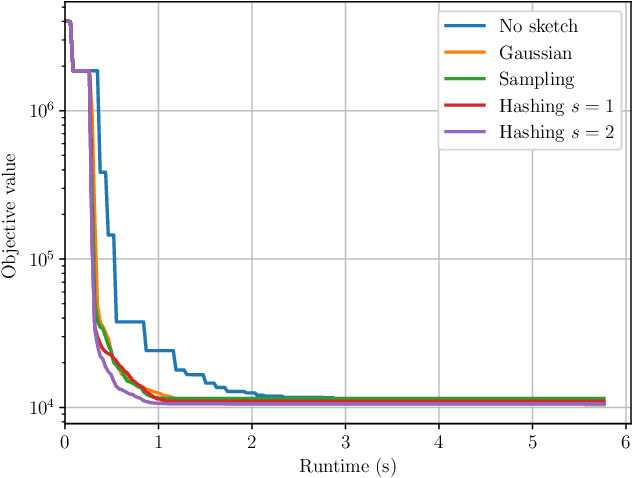
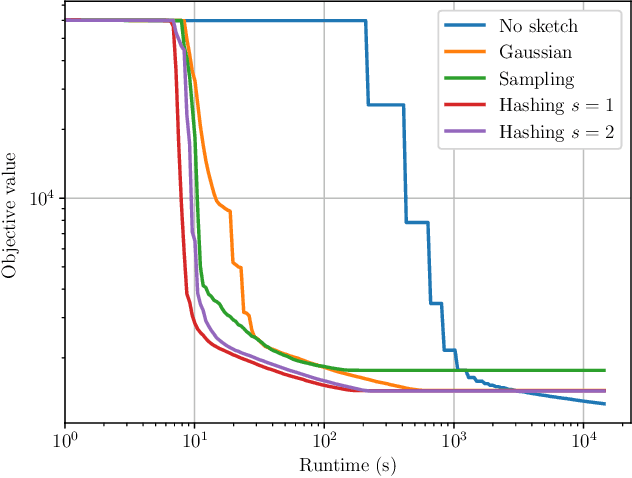
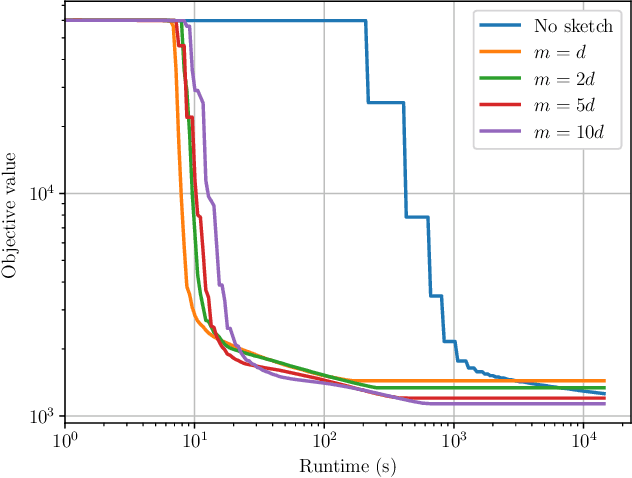
Derivative-free - or zeroth-order - optimization (DFO) has gained recent attention for its ability to solve problems in a variety of application areas, including machine learning, particularly involving objectives which are stochastic and/or expensive to compute. In this work, we develop a novel model-based DFO method for solving nonlinear least-squares problems. We improve on state-of-the-art DFO by performing dimensionality reduction in the observational space using sketching methods, avoiding the construction of a full local model. Our approach has a per-iteration computational cost which is linear in problem dimension in a big data regime, and numerical evidence demonstrates that, compared to existing software, it has dramatically improved runtime performance on overdetermined least-squares problems.

Inexact Derivative-Free Optimization for Bilevel Learning

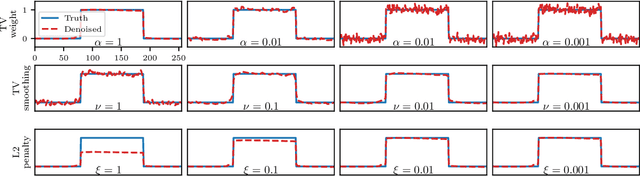
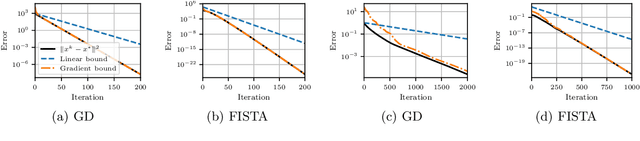
Variational regularization techniques are dominant in the field of mathematical imaging. A drawback of these techniques is that they are dependent on a number of parameters which have to be set by the user. A by now common strategy to resolve this issue is to learn these parameters from data. While mathematically appealing this strategy leads to a nested optimization problem (known as bilevel optimization) which is computationally very difficult to handle. A key ingredient in solving the upper-level problem is the exact solution of the lower-level problem which is practically infeasible. In this work we propose to solve these problems using inexact derivative-free optimization algorithms which never require to solve the lower-level problem exactly. We provide global convergence and worst-case complexity analysis of our approach, and test our proposed framework on ROF-denoising and learning MRI sampling patterns. Dynamically adjusting the lower-level accuracy yields learned parameters with similar reconstruction quality as high-accuracy evaluations but with dramatic reductions in computational work (up to 100 times faster in some cases).