Chuanfei Dong
Data-Driven Modeling of Landau Damping by Physics-Informed Neural Networks
Nov 02, 2022



Abstract:Kinetic approaches are generally accurate in dealing with microscale plasma physics problems but are computationally expensive for large-scale or multiscale systems. One of the long-standing problems in plasma physics is the integration of kinetic physics into fluid models, which is often achieved through sophisticated analytical closure terms. In this study, we successfully construct a multi-moment fluid model with an implicit fluid closure included in the neural network using machine learning. The multi-moment fluid model is trained with a small fraction of sparsely sampled data from kinetic simulations of Landau damping, using the physics-informed neural network (PINN) and the gradient-enhanced physics-informed neural network (gPINN). The multi-moment fluid model constructed using either PINN or gPINN reproduces the time evolution of the electric field energy, including its damping rate, and the plasma dynamics from the kinetic simulations. For the first time, we introduce a new variant of the gPINN architecture, namely, gPINN$p$ to capture the Landau damping process. Instead of including the gradients of all the equation residuals, gPINN$p$ only adds the gradient of the pressure equation residual as one additional constraint. Among the three approaches, the gPINN$p$-constructed multi-moment fluid model offers the most accurate results. This work sheds new light on the accurate and efficient modeling of large-scale systems, which can be extended to complex multiscale laboratory, space, and astrophysical plasma physics problems.
Data-driven, multi-moment fluid modeling of Landau damping
Sep 10, 2022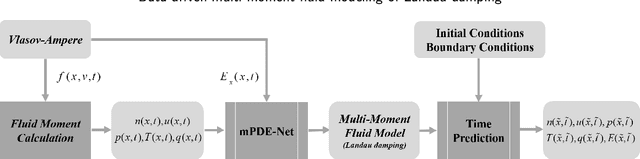

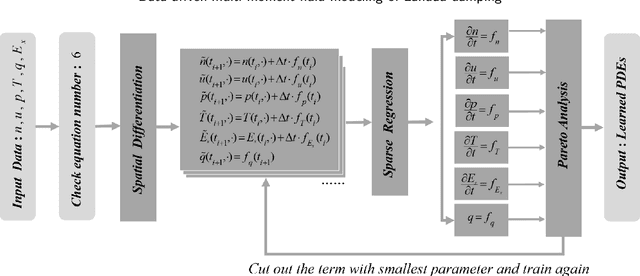
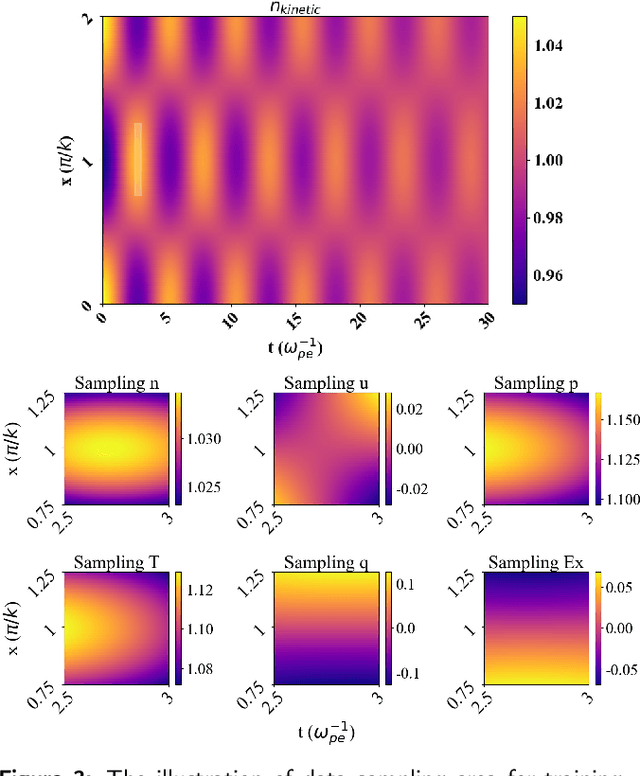
Abstract:Deriving governing equations of complex physical systems based on first principles can be quite challenging when there are certain unknown terms and hidden physical mechanisms in the systems. In this work, we apply a deep learning architecture to learn fluid partial differential equations (PDEs) of a plasma system based on the data acquired from a fully kinetic model. The learned multi-moment fluid PDEs are demonstrated to incorporate kinetic effects such as Landau damping. Based on the learned fluid closure, the data-driven, multi-moment fluid modeling can well reproduce all the physical quantities derived from the fully kinetic model. The calculated damping rate of Landau damping is consistent with both the fully kinetic simulation and the linear theory. The data-driven fluid modeling of PDEs for complex physical systems may be applied to improve fluid closure and reduce the computational cost of multi-scale modeling of global systems.
Algorithms and Statistical Models for Scientific Discovery in the Petabyte Era
Nov 05, 2019Abstract:The field of astronomy has arrived at a turning point in terms of size and complexity of both datasets and scientific collaboration. Commensurately, algorithms and statistical models have begun to adapt --- e.g., via the onset of artificial intelligence --- which itself presents new challenges and opportunities for growth. This white paper aims to offer guidance and ideas for how we can evolve our technical and collaborative frameworks to promote efficient algorithmic development and take advantage of opportunities for scientific discovery in the petabyte era. We discuss challenges for discovery in large and complex data sets; challenges and requirements for the next stage of development of statistical methodologies and algorithmic tool sets; how we might change our paradigms of collaboration and education; and the ethical implications of scientists' contributions to widely applicable algorithms and computational modeling. We start with six distinct recommendations that are supported by the commentary following them. This white paper is related to a larger corpus of effort that has taken place within and around the Petabytes to Science Workshops (https://petabytestoscience.github.io/).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge