Toward Optimal Search and Retrieval for RAG

Retrieval-augmented generation (RAG) is a promising method for addressing some of the memory-related challenges associated with Large Language Models (LLMs). Two separate systems form the RAG pipeline, the retriever and the reader, and the impact of each on downstream task performance is not well-understood. Here, we work towards the goal of understanding how retrievers can be optimized for RAG pipelines for common tasks such as Question Answering (QA). We conduct experiments focused on the relationship between retrieval and RAG performance on QA and attributed QA and unveil a number of insights useful to practitioners developing high-performance RAG pipelines. For example, lowering search accuracy has minor implications for RAG performance while potentially increasing retrieval speed and memory efficiency.

Locally-Adaptive Quantization for Streaming Vector Search

Retrieving the most similar vector embeddings to a given query among a massive collection of vectors has long been a key component of countless real-world applications. The recently introduced Retrieval-Augmented Generation is one of the most prominent examples. For many of these applications, the database evolves over time by inserting new data and removing outdated data. In these cases, the retrieval problem is known as streaming similarity search. While Locally-Adaptive Vector Quantization (LVQ), a highly efficient vector compression method, yields state-of-the-art search performance for non-evolving databases, its usefulness in the streaming setting has not been yet established. In this work, we study LVQ in streaming similarity search. In support of our evaluation, we introduce two improvements of LVQ: Turbo LVQ and multi-means LVQ that boost its search performance by up to 28% and 27%, respectively. Our studies show that LVQ and its new variants enable blazing fast vector search, outperforming its closest competitor by up to 9.4x for identically distributed data and by up to 8.8x under the challenging scenario of data distribution shifts (i.e., where the statistical distribution of the data changes over time). We release our contributions as part of Scalable Vector Search, an open-source library for high-performance similarity search.

LeanVec: Search your vectors faster by making them fit

Modern deep learning models have the ability to generate high-dimensional vectors whose similarity reflects semantic resemblance. Thus, similarity search, i.e., the operation of retrieving those vectors in a large collection that are similar to a given query, has become a critical component of a wide range of applications that demand highly accurate and timely answers. In this setting, the high vector dimensionality puts similarity search systems under compute and memory pressure, leading to subpar performance. Additionally, cross-modal retrieval tasks have become increasingly common, e.g., where a user inputs a text query to find the most relevant images for that query. However, these queries often have different distributions than the database embeddings, making it challenging to achieve high accuracy. In this work, we present LeanVec, a framework that combines linear dimensionality reduction with vector quantization to accelerate similarity search on high-dimensional vectors while maintaining accuracy. We present LeanVec variants for in-distribution (ID) and out-of-distribution (OOD) queries. LeanVec-ID yields accuracies on par with those from recently introduced deep learning alternatives whose computational overhead precludes their usage in practice. LeanVec-OOD uses a novel technique for dimensionality reduction that considers the query and database distributions to simultaneously boost the accuracy and the performance of the framework even further (even presenting competitive results when the query and database distributions match). All in all, our extensive and varied experimental results show that LeanVec produces state-of-the-art results, with up to 3.7x improvement in search throughput and up to 4.9x faster index build time over the state of the art.

Similarity search in the blink of an eye with compressed indices

Nowadays, data is represented by vectors. Retrieving those vectors, among millions and billions, that are similar to a given query is a ubiquitous problem of relevance for a wide range of applications. In this work, we present new techniques for creating faster and smaller indices to run these searches. To this end, we introduce a novel vector compression method, Locally-adaptive Vector Quantization (LVQ), that simultaneously reduces memory footprint and improves search performance, with minimal impact on search accuracy. LVQ is designed to work optimally in conjunction with graph-based indices, reducing their effective bandwidth while enabling random-access-friendly fast similarity computations. Our experimental results show that LVQ, combined with key optimizations for graph-based indices in modern datacenter systems, establishes the new state of the art in terms of performance and memory footprint. For billions of vectors, LVQ outcompetes the second-best alternatives: (1) in the low-memory regime, by up to 20.7x in throughput with up to a 3x memory footprint reduction, and (2) in the high-throughput regime by 5.8x with 1.4x less memory.

A Bayesian Hyperprior Approach for Joint Image Denoising and Interpolation, with an Application to HDR Imaging

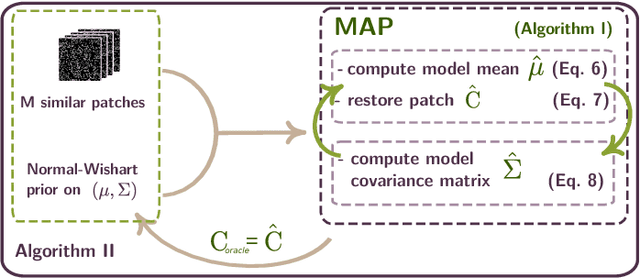
Recently, impressive denoising results have been achieved by Bayesian approaches which assume Gaussian models for the image patches. This improvement in performance can be attributed to the use of per-patch models. Unfortunately such an approach is particularly unstable for most inverse problems beyond denoising. In this work, we propose the use of a hyperprior to model image patches, in order to stabilize the estimation procedure. There are two main advantages to the proposed restoration scheme: Firstly it is adapted to diagonal degradation matrices, and in particular to missing data problems (e.g. inpainting of missing pixels or zooming). Secondly it can deal with signal dependent noise models, particularly suited to digital cameras. As such, the scheme is especially adapted to computational photography. In order to illustrate this point, we provide an application to high dynamic range imaging from a single image taken with a modified sensor, which shows the effectiveness of the proposed scheme.

Probabilistic Fluorescence-Based Synapse Detection

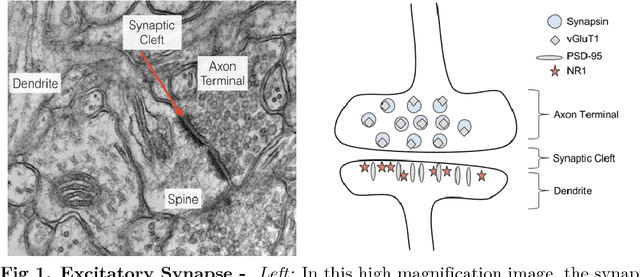
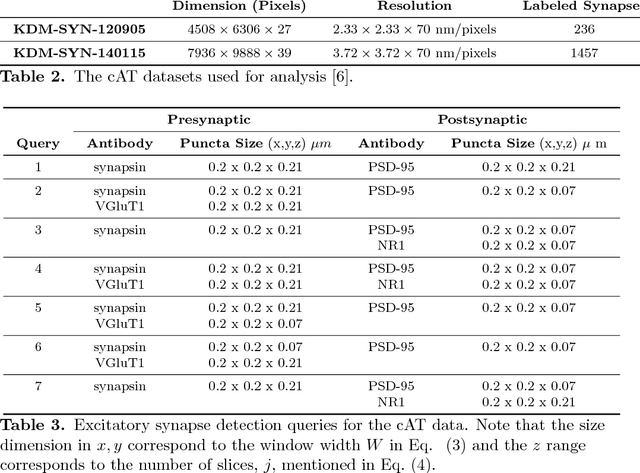
Brain function results from communication between neurons connected by complex synaptic networks. Synapses are themselves highly complex and diverse signaling machines, containing protein products of hundreds of different genes, some in hundreds of copies, arranged in precise lattice at each individual synapse. Synapses are fundamental not only to synaptic network function but also to network development, adaptation, and memory. In addition, abnormalities of synapse numbers or molecular components are implicated in most mental and neurological disorders. Despite their obvious importance, mammalian synapse populations have so far resisted detailed quantitative study. In human brains and most animal nervous systems, synapses are very small and very densely packed: there are approximately 1 billion synapses per cubic millimeter of human cortex. This volumetric density poses very substantial challenges to proteometric analysis at the critical level of the individual synapse. The present work describes new probabilistic image analysis methods for single-synapse analysis of synapse populations in both animal and human brains.

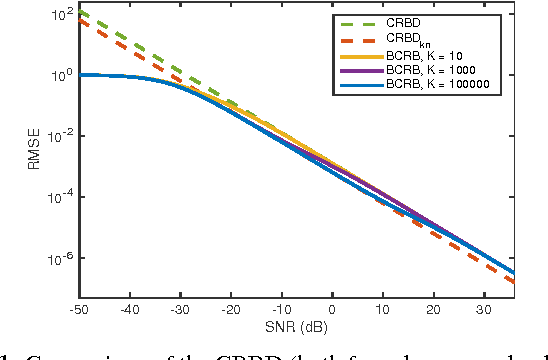
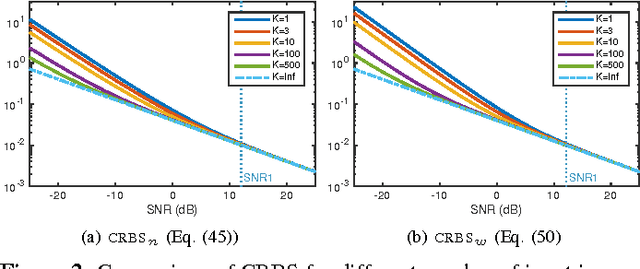
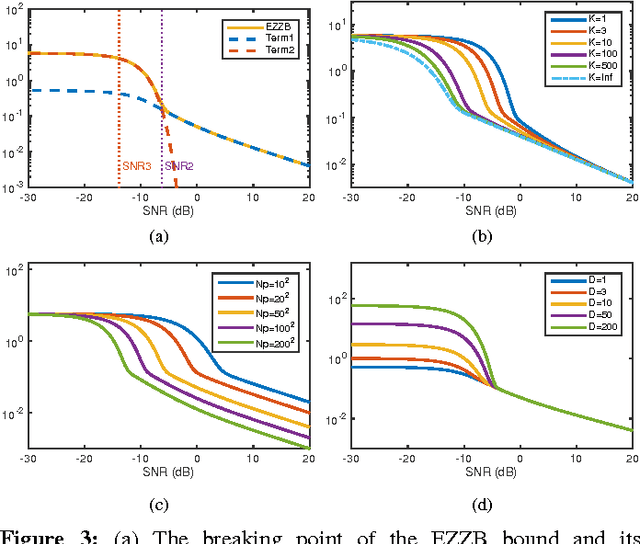
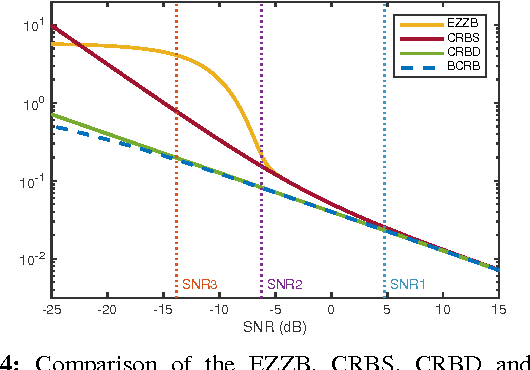
Fundamental Limits in Multi-image Alignment

The performance of multi-image alignment, bringing different images into one coordinate system, is critical in many applications with varied signal-to-noise ratio (SNR) conditions. A great amount of effort is being invested into developing methods to solve this problem. Several important questions thus arise, including: Which are the fundamental limits in multi-image alignment performance? Does having access to more images improve the alignment? Theoretical bounds provide a fundamental benchmark to compare methods and can help establish whether improvements can be made. In this work, we tackle the problem of finding the performance limits in image registration when multiple shifted and noisy observations are available. We derive and analyze the Cram\'er-Rao and Ziv-Zakai lower bounds under different statistical models for the underlying image. The accuracy of the derived bounds is experimentally assessed through a comparison to the maximum likelihood estimator. We show the existence of different behavior zones depending on the difficulty level of the problem, given by the SNR conditions of the input images. We find that increasing the number of images is only useful below a certain SNR threshold, above which the pairwise MLE estimation proves to be optimal. The analysis we present here brings further insight into the fundamental limitations of the multi-image alignment problem.