Reducing base drag on road vehicles using pulsed jets optimized by hybrid genetic algorithms

Aerodynamic drag on flat-backed vehicles like vans and trucks is dominated by a low-pressure wake, whose control is critical for reducing fuel consumption. This paper presents an experimental study at $Re_W\approx 78,300$ on active flow control using four pulsed jets at the rear edges of a bluff body model. A hybrid genetic algorithm, combining a global search with a local gradient-based optimizer, was used to determine the optimal jet actuation parameters in an experiment-in-the-loop setup. The cost function was designed to achieve a net energy saving by simultaneously minimizing aerodynamic drag and penalizing the actuation's energy consumption. The optimization campaign successfully identified a control strategy that yields a drag reduction of approximately 10%. The optimal control law features a strong, low-frequency actuation from the bottom jet, which targets the main vortex shedding, while the top and lateral jets address higher-frequency, less energetic phenomena. Particle Image Velocimetry analysis reveals a significant upward shift and stabilization of the wake, leading to substantial pressure recovery on the model's lower base. Ultimately, this work demonstrates that a model-free optimization approach can successfully identify non-intuitive, multi-faceted actuation strategies that yield significant and energetically efficient drag reduction.

Towards aerodynamic surrogate modeling based on $β$-variational autoencoders

Surrogate models combining dimensionality reduction and regression techniques are essential to reduce the need for costly high-fidelity CFD data. New approaches using $\beta$-Variational Autoencoder ($\beta$-VAE) architectures have shown promise in obtaining high-quality low-dimensional representations of high-dimensional flow data while enabling physical interpretation of their latent spaces. We propose a surrogate model based on latent space regression to predict pressure distributions on a transonic wing given the flight conditions: Mach number and angle of attack. The $\beta$-VAE model, enhanced with Principal Component Analysis (PCA), maps high-dimensional data to a low-dimensional latent space, showing a direct correlation with flight conditions. Regularization through $\beta$ requires careful tuning to improve the overall performance, while PCA pre-processing aids in constructing an effective latent space, improving autoencoder training and performance. Gaussian Process Regression is used to predict latent space variables from flight conditions, showing robust behavior independent of $\beta$, and the decoder reconstructs the high-dimensional pressure field data. This pipeline provides insight into unexplored flight conditions. Additionally, a fine-tuning process of the decoder further refines the model, reducing dependency on $\beta$ and enhancing accuracy. The structured latent space, robust regression performance, and significant improvements from fine-tuning collectively create a highly accurate and efficient surrogate model. Our methodology demonstrates the effectiveness of $\beta$-VAEs for aerodynamic surrogate modeling, offering a rapid, cost-effective, and reliable alternative for aerodynamic data prediction.

$β$-Variational autoencoders and transformers for reduced-order modelling of fluid flows

Variational autoencoder (VAE) architectures have the potential to develop reduced-order models (ROMs) for chaotic fluid flows. We propose a method for learning compact and near-orthogonal ROMs using a combination of a $\beta$-VAE and a transformer, tested on numerical data from a two-dimensional viscous flow in both periodic and chaotic regimes. The $\beta$-VAE is trained to learn a compact latent representation of the flow velocity, and the transformer is trained to predict the temporal dynamics in latent space. Using the $\beta$-VAE to learn disentangled representations in latent-space, we obtain a more interpretable flow model with features that resemble those observed in the proper orthogonal decomposition, but with a more efficient representation. Using Poincar\'e maps, the results show that our method can capture the underlying dynamics of the flow outperforming other prediction models. The proposed method has potential applications in other fields such as weather forecasting, structural dynamics or biomedical engineering.

Super-resolution GANs of randomly-seeded fields

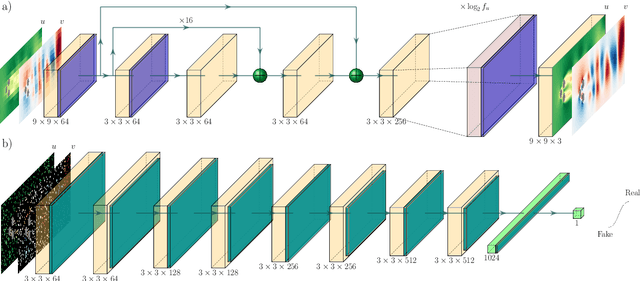
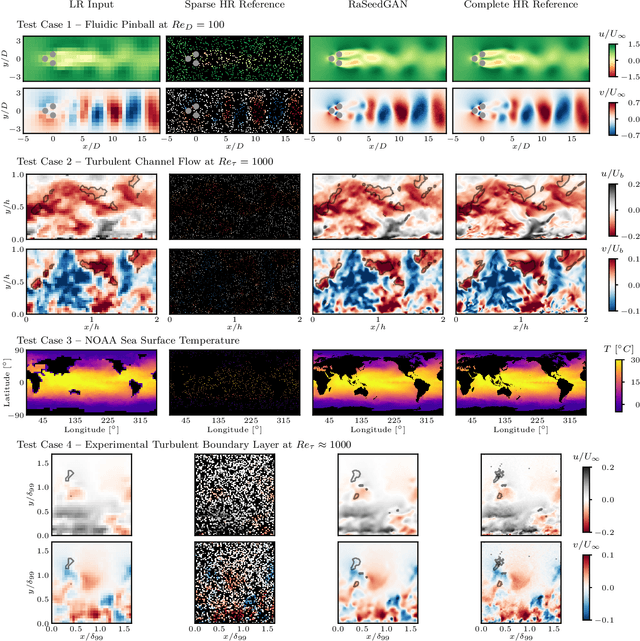
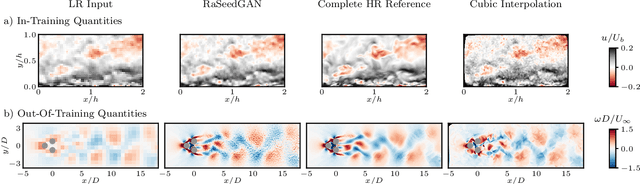
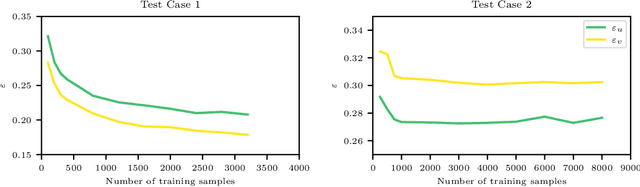
Reconstruction of field quantities from sparse measurements is a problem arising in a broad spectrum of applications. This task is particularly challenging when mapping between point sparse measurements and field quantities shall be performed in an unsupervised manner. Further complexity is added for moving sensors and/or random on-off status. Under such conditions, the most straightforward solution is to interpolate the scattered data onto a regular grid. However, the spatial resolution achieved with this approach is ultimately limited by the mean spacing between the sparse measurements. In this work, we propose a novel super-resolution generative adversarial network (GAN) framework to estimate field quantities from random sparse sensors without needing any full-resolution field for training. The algorithm exploits random sampling to provide incomplete views of the high-resolution underlying distributions. It is hereby referred to as RAndomly-SEEDed super-resolution GAN (RaSeedGAN). The proposed technique is tested on synthetic databases of fluid flow simulations, ocean surface temperature distributions measurements, and particle image velocimetry data of a zero-pressure-gradient turbulent boundary layer. The results show an excellent performance of the proposed methodology even in cases with a high level of gappyness (>50\%) or noise conditions. To our knowledge, this is the first super-resolution GANs algorithm for full-field estimation from randomly-seeded fields with no need of a full-field high-resolution representation during training nor of a library of training examples.