TIMEST: Temporal Information Motif Estimator Using Sampling Trees

The mining of pattern subgraphs, known as motifs, is a core task in the field of graph mining. Edges in real-world networks often have timestamps, so there is a need for temporal motif mining. A temporal motif is a richer structure that imposes timing constraints on the edges of the motif. Temporal motifs have been used to analyze social networks, financial transactions, and biological networks. Motif counting in temporal graphs is particularly challenging. A graph with millions of edges can have trillions of temporal motifs, since the same edge can occur with multiple timestamps. There is a combinatorial explosion of possibilities, and state-of-the-art algorithms cannot manage motifs with more than four vertices. In this work, we present TIMEST: a general, fast, and accurate estimation algorithm to count temporal motifs of arbitrary sizes in temporal networks. Our approach introduces a temporal spanning tree sampler that leverages weighted sampling to generate substructures of target temporal motifs. This method carefully takes a subset of temporal constraints of the motif that can be jointly and efficiently sampled. TIMEST uses randomized estimation techniques to obtain accurate estimates of motif counts. We give theoretical guarantees on the running time and approximation guarantees of TIMEST. We perform an extensive experimental evaluation and show that TIMEST is both faster and more accurate than previous algorithms. Our CPU implementation exhibits an average speedup of 28x over state-of-the-art GPU implementation of the exact algorithm, and 6x speedup over SOTA approximate algorithms while consistently showcasing less than 5% error in most cases. For example, TIMEST can count the number of instances of a financial fraud temporal motif in four minutes with 0.6% error, while exact methods take more than two days.

Triadic First-Order Logic Queries in Temporal Networks

Motif counting is a fundamental problem in network analysis, and there is a rich literature of theoretical and applied algorithms for this problem. Given a large input network $G$, a motif $H$ is a small "pattern" graph indicative of special local structure. Motif/pattern mining involves finding all matches of this pattern in the input $G$. The simplest, yet challenging, case of motif counting is when $H$ has three vertices, often called a "triadic" query. Recent work has focused on "temporal graph mining", where the network $G$ has edges with timestamps (and directions) and $H$ has time constraints. Inspired by concepts in logic and database theory, we introduce the study of "thresholded First Order Logic (FOL) Motif Analysis" for massive temporal networks. A typical triadic motif query asks for the existence of three vertices that form a desired temporal pattern. An "FOL" motif query is obtained by having both existential and thresholded universal quantifiers. This allows for query semantics that can mine richer information from networks. A typical triadic query would be "find all triples of vertices $u,v,w$ such that they form a triangle within one hour". A thresholded FOL query can express "find all pairs $u,v$ such that for half of $w$ where $(u,w)$ formed an edge, $(v,w)$ also formed an edge within an hour". We design the first algorithm, FOLTY, for mining thresholded FOL triadic queries. The theoretical running time of FOLTY matches the best known running time for temporal triangle counting in sparse graphs. We give an efficient implementation of FOLTY using specialized temporal data structures. FOLTY has excellent empirical behavior, and can answer triadic FOL queries on graphs with nearly 70M edges is less than hour on commodity hardware. Our work has the potential to start a new research direction in the classic well-studied problem of motif analysis.

Monotonicity Testing of High-Dimensional Distributions with Subcube Conditioning

We study monotonicity testing of high-dimensional distributions on $\{-1,1\}^n$ in the model of subcube conditioning, suggested and studied by Canonne, Ron, and Servedio~\cite{CRS15} and Bhattacharyya and Chakraborty~\cite{BC18}. Previous work shows that the \emph{sample complexity} of monotonicity testing must be exponential in $n$ (Rubinfeld, Vasilian~\cite{RV20}, and Aliakbarpour, Gouleakis, Peebles, Rubinfeld, Yodpinyanee~\cite{AGPRY19}). We show that the subcube \emph{query complexity} is $\tilde{\Theta}(n/\varepsilon^2)$, by proving nearly matching upper and lower bounds. Our work is the first to use directed isoperimetric inequalities (developed for function monotonicity testing) for analyzing a distribution testing algorithm. Along the way, we generalize an inequality of Khot, Minzer, and Safra~\cite{KMS18} to real-valued functions on $\{-1,1\}^n$. We also study uniformity testing of distributions that are promised to be monotone, a problem introduced by Rubinfeld, Servedio~\cite{RS09} , using subcube conditioning. We show that the query complexity is $\tilde{\Theta}(\sqrt{n}/\varepsilon^2)$. Our work proves the lower bound, which matches (up to poly-logarithmic factors) the uniformity testing upper bound for general distributions (Canonne, Chen, Kamath, Levi, Waingarten~\cite{CCKLW21}). Hence, we show that monotonicity does not help, beyond logarithmic factors, in testing uniformity of distributions with subcube conditional queries.

Accurate and Fast Estimation of Temporal Motifs using Path Sampling

Counting the number of small subgraphs, called motifs, is a fundamental problem in social network analysis and graph mining. Many real-world networks are directed and temporal, where edges have timestamps. Motif counting in directed, temporal graphs is especially challenging because there are a plethora of different kinds of patterns. Temporal motif counts reveal much richer information and there is a need for scalable algorithms for motif counting. A major challenge in counting is that there can be trillions of temporal motif matches even with a graph with only millions of vertices. Both the motifs and the input graphs can have multiple edges between two vertices, leading to a combinatorial explosion problem. Counting temporal motifs involving just four vertices is not feasible with current state-of-the-art algorithms. We design an algorithm, TEACUPS, that addresses this problem using a novel technique of temporal path sampling. We combine a path sampling method with carefully designed temporal data structures, to propose an efficient approximate algorithm for temporal motif counting. TEACUPS is an unbiased estimator with provable concentration behavior, which can be used to bound the estimation error. For a Bitcoin graph with hundreds of millions of edges, TEACUPS runs in less than 1 minute, while the exact counting algorithm takes more than a day. We empirically demonstrate the accuracy of TEACUPS on large datasets, showing an average of 30$\times$ speedup (up to 2000$\times$ speedup) compared to existing GPU-based exact counting methods while preserving high count estimation accuracy.

Covering a Graph with Dense Subgraph Families, via Triangle-Rich Sets

Graphs are a fundamental data structure used to represent relationships in domains as diverse as the social sciences, bioinformatics, cybersecurity, the Internet, and more. One of the central observations in network science is that real-world graphs are globally sparse, yet contains numerous "pockets" of high edge density. A fundamental task in graph mining is to discover these dense subgraphs. Most common formulations of the problem involve finding a single (or a few) "optimally" dense subsets. But in most real applications, one does not care for the optimality. Instead, we want to find a large collection of dense subsets that covers a significant fraction of the input graph. We give a mathematical formulation of this problem, using a new definition of regularly triangle-rich (RTR) families. These families capture the notion of dense subgraphs that contain many triangles and have degrees comparable to the subgraph size. We design a provable algorithm, RTRExtractor, that can discover RTR families that approximately cover any RTR set. The algorithm is efficient and is inspired by recent results that use triangle counts for community testing and clustering. We show that RTRExtractor has excellent behavior on a large variety of real-world datasets. It is able to process graphs with hundreds of millions of edges within minutes. Across many datasets, RTRExtractor achieves high coverage using high edge density datasets. For example, the output covers a quarter of the vertices with subgraphs of edge density more than (say) $0.5$, for datasets with 10M+ edges. We show an example of how the output of RTRExtractor correlates with meaningful sets of similar vertices in a citation network, demonstrating the utility of RTRExtractor for unsupervised graph discovery tasks.

Classic Graph Structural Features Outperform Factorization-Based Graph Embedding Methods on Community Labeling

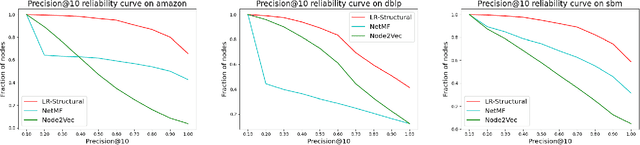
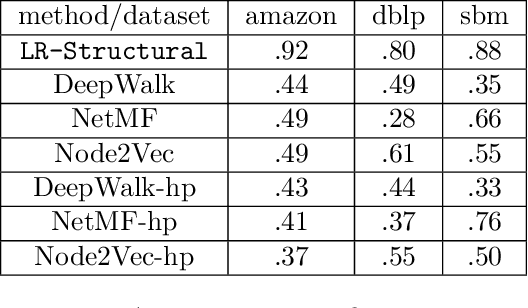
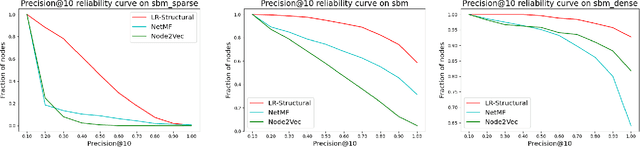
Graph representation learning (also called graph embeddings) is a popular technique for incorporating network structure into machine learning models. Unsupervised graph embedding methods aim to capture graph structure by learning a low-dimensional vector representation (the embedding) for each node. Despite the widespread use of these embeddings for a variety of downstream transductive machine learning tasks, there is little principled analysis of the effectiveness of this approach for common tasks. In this work, we provide an empirical and theoretical analysis for the performance of a class of embeddings on the common task of pairwise community labeling. This is a binary variant of the classic community detection problem, which seeks to build a classifier to determine whether a pair of vertices participate in a community. In line with our goal of foundational understanding, we focus on a popular class of unsupervised embedding techniques that learn low rank factorizations of a vertex proximity matrix (this class includes methods like GraRep, DeepWalk, node2vec, NetMF). We perform detailed empirical analysis for community labeling over a variety of real and synthetic graphs with ground truth. In all cases we studied, the models trained from embedding features perform poorly on community labeling. In constrast, a simple logistic model with classic graph structural features handily outperforms the embedding models. For a more principled understanding, we provide a theoretical analysis for the (in)effectiveness of these embeddings in capturing the community structure. We formally prove that popular low-dimensional factorization methods either cannot produce community structure, or can only produce ``unstable" communities. These communities are inherently unstable under small perturbations.

Randomized Algorithms for Scientific Computing (RASC)

Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

The impossibility of low rank representations for triangle-rich complex networks

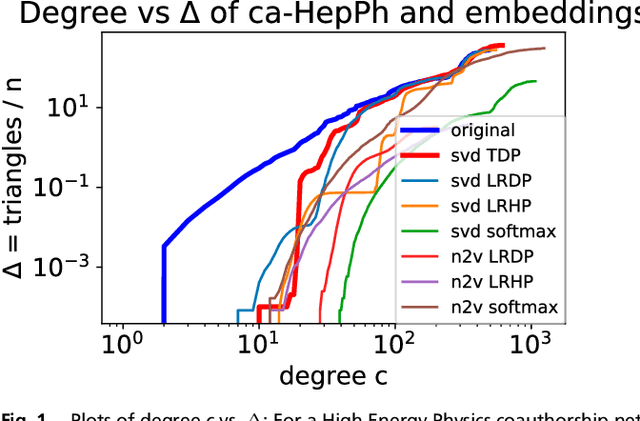
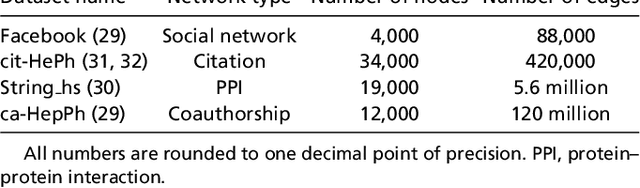
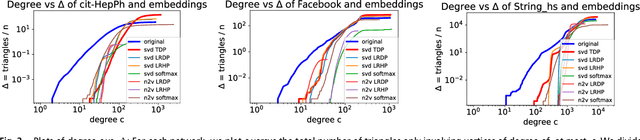
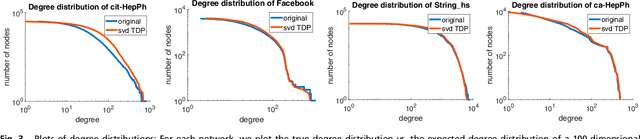
The study of complex networks is a significant development in modern science, and has enriched the social sciences, biology, physics, and computer science. Models and algorithms for such networks are pervasive in our society, and impact human behavior via social networks, search engines, and recommender systems to name a few. A widely used algorithmic technique for modeling such complex networks is to construct a low-dimensional Euclidean embedding of the vertices of the network, where proximity of vertices is interpreted as the likelihood of an edge. Contrary to the common view, we argue that such graph embeddings do not}capture salient properties of complex networks. The two properties we focus on are low degree and large clustering coefficients, which have been widely established to be empirically true for real-world networks. We mathematically prove that any embedding (that uses dot products to measure similarity) that can successfully create these two properties must have rank nearly linear in the number of vertices. Among other implications, this establishes that popular embedding techniques such as Singular Value Decomposition and node2vec fail to capture significant structural aspects of real-world complex networks. Furthermore, we empirically study a number of different embedding techniques based on dot product, and show that they all fail to capture the triangle structure.

Influence and Dynamic Behavior in Random Boolean Networks

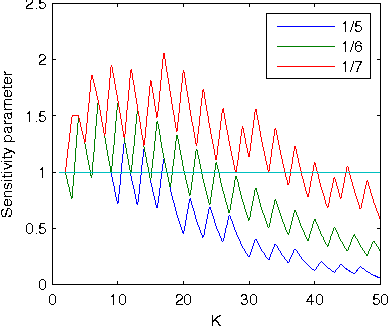
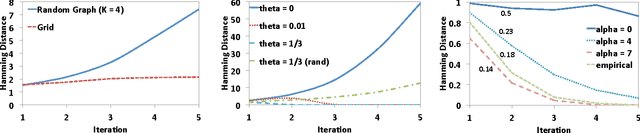
We present a rigorous mathematical framework for analyzing dynamics of a broad class of Boolean network models. We use this framework to provide the first formal proof of many of the standard critical transition results in Boolean network analysis, and offer analogous characterizations for novel classes of random Boolean networks. We precisely connect the short-run dynamic behavior of a Boolean network to the average influence of the transfer functions. We show that some of the assumptions traditionally made in the more common mean-field analysis of Boolean networks do not hold in general. For example, we offer some evidence that imbalance, or expected internal inhomogeneity, of transfer functions is a crucial feature that tends to drive quiescent behavior far more strongly than previously observed.