Depthwise Hyperparameter Transfer in Residual Networks: Dynamics and Scaling Limit

The cost of hyperparameter tuning in deep learning has been rising with model sizes, prompting practitioners to find new tuning methods using a proxy of smaller networks. One such proposal uses $\mu$P parameterized networks, where the optimal hyperparameters for small width networks transfer to networks with arbitrarily large width. However, in this scheme, hyperparameters do not transfer across depths. As a remedy, we study residual networks with a residual branch scale of $1/\sqrt{\text{depth}}$ in combination with the $\mu$P parameterization. We provide experiments demonstrating that residual architectures including convolutional ResNets and Vision Transformers trained with this parameterization exhibit transfer of optimal hyperparameters across width and depth on CIFAR-10 and ImageNet. Furthermore, our empirical findings are supported and motivated by theory. Using recent developments in the dynamical mean field theory (DMFT) description of neural network learning dynamics, we show that this parameterization of ResNets admits a well-defined feature learning joint infinite-width and infinite-depth limit and show convergence of finite-size network dynamics towards this limit.

Les Houches Lectures on Deep Learning at Large & Infinite Width

These lectures, presented at the 2022 Les Houches Summer School on Statistical Physics and Machine Learning, focus on the infinite-width limit and large-width regime of deep neural networks. Topics covered include various statistical and dynamical properties of these networks. In particular, the lecturers discuss properties of random deep neural networks; connections between trained deep neural networks, linear models, kernels, and Gaussian processes that arise in the infinite-width limit; and perturbative and non-perturbative treatments of large but finite-width networks, at initialization and after training.

Quantitative CLTs in Deep Neural Networks

We study the distribution of a fully connected neural network with random Gaussian weights and biases in which the hidden layer widths are proportional to a large constant $n$. Under mild assumptions on the non-linearity, we obtain quantitative bounds on normal approximations valid at large but finite $n$ and any fixed network depth. Our theorems show both for the finite-dimensional distributions and the entire process, that the distance between a random fully connected network (and its derivatives) to the corresponding infinite width Gaussian process scales like $n^{-\gamma}$ for $\gamma>0$, with the exponent depending on the metric used to measure discrepancy. Our bounds are strictly stronger in terms of their dependence on network width than any previously available in the literature; in the one-dimensional case, we also prove that they are optimal, i.e., we establish matching lower bounds.

Principles for Initialization and Architecture Selection in Graph Neural Networks with ReLU Activations

This article derives and validates three principles for initialization and architecture selection in finite width graph neural networks (GNNs) with ReLU activations. First, we theoretically derive what is essentially the unique generalization to ReLU GNNs of the well-known He-initialization. Our initialization scheme guarantees that the average scale of network outputs and gradients remains order one at initialization. Second, we prove in finite width vanilla ReLU GNNs that oversmoothing is unavoidable at large depth when using fixed aggregation operator, regardless of initialization. We then prove that using residual aggregation operators, obtained by interpolating a fixed aggregation operator with the identity, provably alleviates oversmoothing at initialization. Finally, we show that the common practice of using residual connections with a fixup-type initialization provably avoids correlation collapse in final layer features at initialization. Through ablation studies we find that using the correct initialization, residual aggregation operators, and residual connections in the forward pass significantly and reliably speeds up early training dynamics in deep ReLU GNNs on a variety of tasks.

Depth Dependence of $μ$P Learning Rates in ReLU MLPs

In this short note we consider random fully connected ReLU networks of width $n$ and depth $L$ equipped with a mean-field weight initialization. Our purpose is to study the dependence on $n$ and $L$ of the maximal update ($\mu$P) learning rate, the largest learning rate for which the mean squared change in pre-activations after one step of gradient descent remains uniformly bounded at large $n,L$. As in prior work on $\mu$P of Yang et. al., we find that this maximal update learning rate is independent of $n$ for all but the first and last layer weights. However, we find that it has a non-trivial dependence of $L$, scaling like $L^{-3/2}.$

Bayesian Interpolation with Deep Linear Networks

This article concerns Bayesian inference using deep linear networks with output dimension one. In the interpolating (zero noise) regime we show that with Gaussian weight priors and MSE negative log-likelihood loss both the predictive posterior and the Bayesian model evidence can be written in closed form in terms of a class of meromorphic special functions called Meijer-G functions. These results are non-asymptotic and hold for any training dataset, network depth, and hidden layer widths, giving exact solutions to Bayesian interpolation using a deep Gaussian process with a Euclidean covariance at each layer. Through novel asymptotic expansions of Meijer-G functions, a rich new picture of the role of depth emerges. Specifically, we find that the posteriors in deep linear networks with data-independent priors are the same as in shallow networks with evidence maximizing data-dependent priors. In this sense, deep linear networks make provably optimal predictions. We also prove that, starting from data-agnostic priors, Bayesian model evidence in wide networks is only maximized at infinite depth. This gives a principled reason to prefer deeper networks (at least in the linear case). Finally, our results show that with data-agnostic priors a novel notion of effective depth given by \[\#\text{hidden layers}\times\frac{\#\text{training data}}{\text{network width}}\] determines the Bayesian posterior in wide linear networks, giving rigorous new scaling laws for generalization error.

Maximal Initial Learning Rates in Deep ReLU Networks

Training a neural network requires choosing a suitable learning rate, involving a trade-off between speed and effectiveness of convergence. While there has been considerable theoretical and empirical analysis of how large the learning rate can be, most prior work focuses only on late-stage training. In this work, we introduce the maximal initial learning rate $\eta^{\ast}$ - the largest learning rate at which a randomly initialized neural network can successfully begin training and achieve (at least) a given threshold accuracy. Using a simple approach to estimate $\eta^{\ast}$, we observe that in constant-width fully-connected ReLU networks, $\eta^{\ast}$ demonstrates different behavior to the maximum learning rate later in training. Specifically, we find that $\eta^{\ast}$ is well predicted as a power of $(\text{depth} \times \text{width})$, provided that (i) the width of the network is sufficiently large compared to the depth, and (ii) the input layer of the network is trained at a relatively small learning rate. We further analyze the relationship between $\eta^{\ast}$ and the sharpness $\lambda_{1}$ of the network at initialization, indicating that they are closely though not inversely related. We formally prove bounds for $\lambda_{1}$ in terms of $(\text{depth} \times \text{width})$ that align with our empirical results.

Deep Architecture Connectivity Matters for Its Convergence: A Fine-Grained Analysis

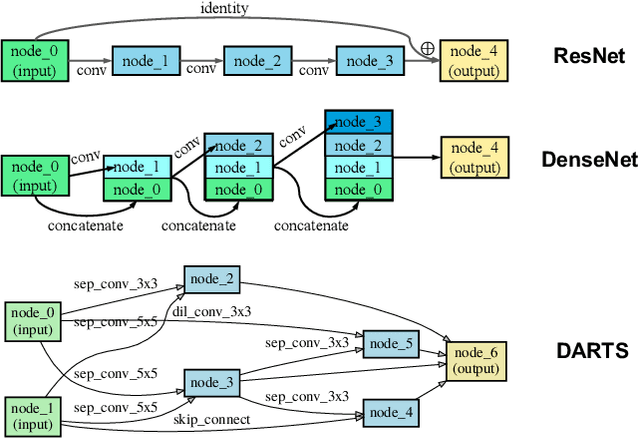
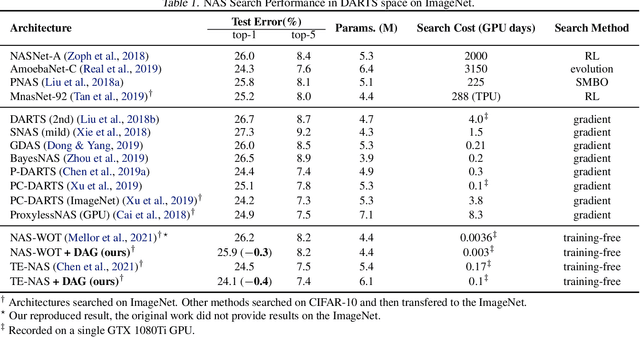
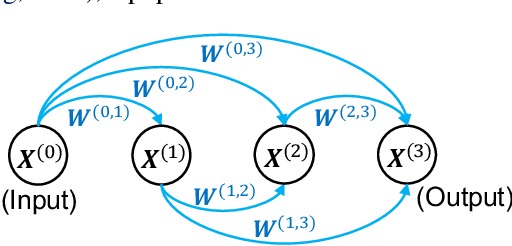
Advanced deep neural networks (DNNs), designed by either human or AutoML algorithms, are growing increasingly complex. Diverse operations are connected by complicated connectivity patterns, e.g., various types of skip connections. Those topological compositions are empirically effective and observed to smooth the loss landscape and facilitate the gradient flow in general. However, it remains elusive to derive any principled understanding of their effects on the DNN capacity or trainability, and to understand why or in which aspect one specific connectivity pattern is better than another. In this work, we theoretically characterize the impact of connectivity patterns on the convergence of DNNs under gradient descent training in fine granularity. By analyzing a wide network's Neural Network Gaussian Process (NNGP), we are able to depict how the spectrum of an NNGP kernel propagates through a particular connectivity pattern, and how that affects the bound of convergence rates. As one practical implication of our results, we show that by a simple filtration on "unpromising" connectivity patterns, we can trim down the number of models to evaluate, and significantly accelerate the large-scale neural architecture search without any overhead. Codes will be released at https://github.com/chenwydj/architecture_convergence.

Correlation Functions in Random Fully Connected Neural Networks at Finite Width

This article considers fully connected neural networks with Gaussian random weights and biases and $L$ hidden layers, each of width proportional to a large parameter $n$. For polynomially bounded non-linearities we give sharp estimates in powers of $1/n$ for the joint correlation functions of the network output and its derivatives. Moreover, we obtain exact layerwise recursions for these correlation functions and solve a number of special cases for classes of non-linearities including $\mathrm{ReLU}$ and $\tanh$. We find in both cases that the depth-to-width ratio $L/n$ plays the role of an effective network depth, controlling both the scale of fluctuations at individual neurons and the size of inter-neuron correlations. We use this to study a somewhat simplified version of the so-called exploding and vanishing gradient problem, proving that this particular variant occurs if and only if $L/n$ is large. Several of the key ideas in this article were first developed at a physics level of rigor in a recent monograph with Roberts and Yaida.

Ridgeless Interpolation with Shallow ReLU Networks in $1D$ is Nearest Neighbor Curvature Extrapolation and Provably Generalizes on Lipschitz Functions

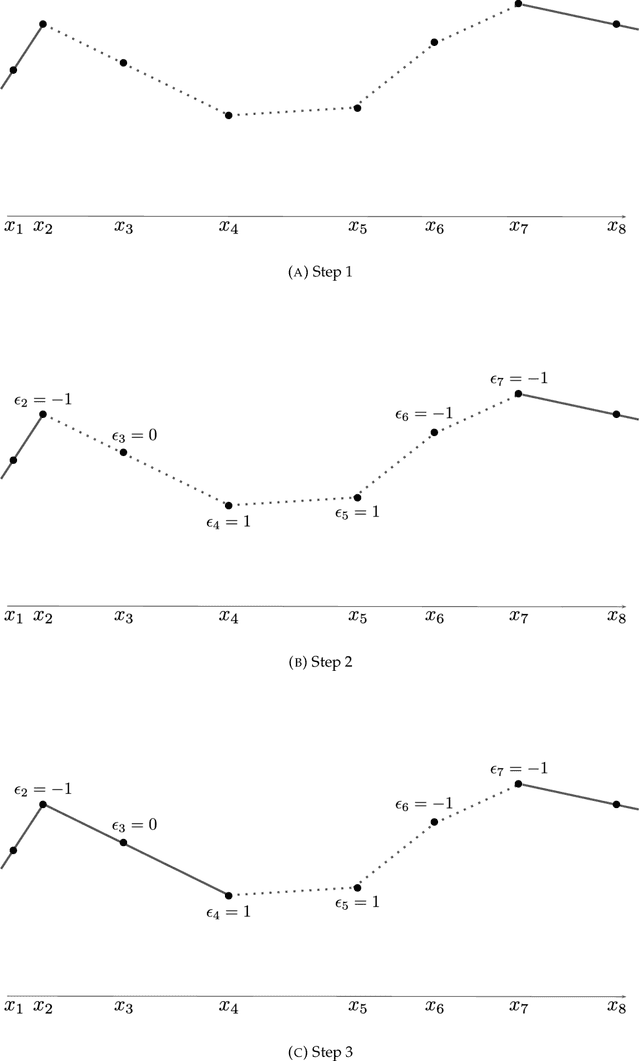
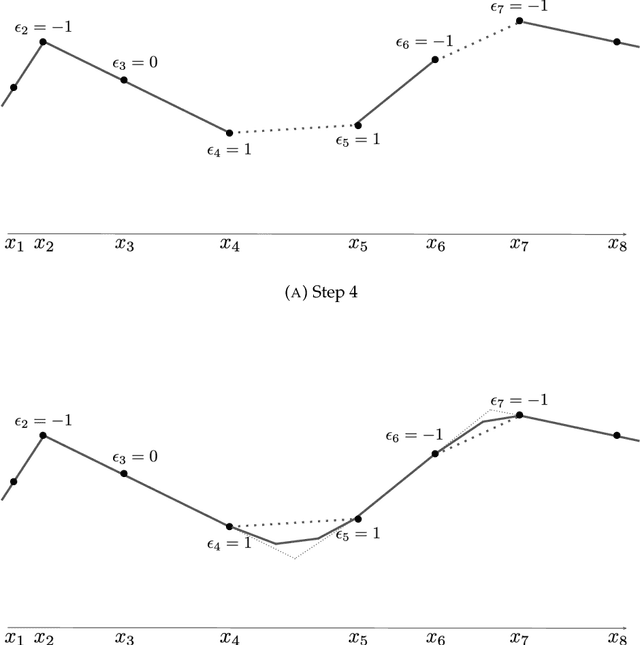
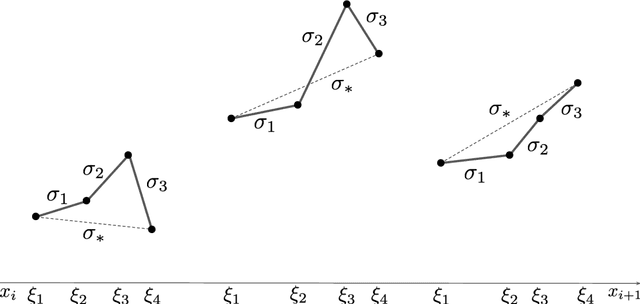
We prove a precise geometric description of all one layer ReLU networks $z(x;\theta)$ with a single linear unit and input/output dimensions equal to one that interpolate a given dataset $\mathcal D=\{(x_i,f(x_i))\}$ and, among all such interpolants, minimize the $\ell_2$-norm of the neuron weights. Such networks can intuitively be thought of as those that minimize the mean-squared error over $\mathcal D$ plus an infinitesimal weight decay penalty. We therefore refer to them as ridgeless ReLU interpolants. Our description proves that, to extrapolate values $z(x;\theta)$ for inputs $x\in (x_i,x_{i+1})$ lying between two consecutive datapoints, a ridgeless ReLU interpolant simply compares the signs of the discrete estimates for the curvature of $f$ at $x_i$ and $x_{i+1}$ derived from the dataset $\mathcal D$. If the curvature estimates at $x_i$ and $x_{i+1}$ have different signs, then $z(x;\theta)$ must be linear on $(x_i,x_{i+1})$. If in contrast the curvature estimates at $x_i$ and $x_{i+1}$ are both positive (resp. negative), then $z(x;\theta)$ is convex (resp. concave) on $(x_i,x_{i+1})$. Our results show that ridgeless ReLU interpolants achieve the best possible generalization for learning $1d$ Lipschitz functions, up to universal constants.