Bayesian Inference with Deep Weakly Nonlinear Networks

We show at a physics level of rigor that Bayesian inference with a fully connected neural network and a shaped nonlinearity of the form $\phi(t) = t + \psi t^3/L$ is (perturbatively) solvable in the regime where the number of training datapoints $P$ , the input dimension $N_0$, the network layer widths $N$, and the network depth $L$ are simultaneously large. Our results hold with weak assumptions on the data; the main constraint is that $P < N_0$. We provide techniques to compute the model evidence and posterior to arbitrary order in $1/N$ and at arbitrary temperature. We report the following results from the first-order computation: 1. When the width $N$ is much larger than the depth $L$ and training set size $P$, neural network Bayesian inference coincides with Bayesian inference using a kernel. The value of $\psi$ determines the curvature of a sphere, hyperbola, or plane into which the training data is implicitly embedded under the feature map. 2. When $LP/N$ is a small constant, neural network Bayesian inference departs from the kernel regime. At zero temperature, neural network Bayesian inference is equivalent to Bayesian inference using a data-dependent kernel, and $LP/N$ serves as an effective depth that controls the extent of feature learning. 3. In the restricted case of deep linear networks ($\psi=0$) and noisy data, we show a simple data model for which evidence and generalization error are optimal at zero temperature. As $LP/N$ increases, both evidence and generalization further improve, demonstrating the benefit of depth in benign overfitting.

Bayesian Interpolation with Deep Linear Networks

This article concerns Bayesian inference using deep linear networks with output dimension one. In the interpolating (zero noise) regime we show that with Gaussian weight priors and MSE negative log-likelihood loss both the predictive posterior and the Bayesian model evidence can be written in closed form in terms of a class of meromorphic special functions called Meijer-G functions. These results are non-asymptotic and hold for any training dataset, network depth, and hidden layer widths, giving exact solutions to Bayesian interpolation using a deep Gaussian process with a Euclidean covariance at each layer. Through novel asymptotic expansions of Meijer-G functions, a rich new picture of the role of depth emerges. Specifically, we find that the posteriors in deep linear networks with data-independent priors are the same as in shallow networks with evidence maximizing data-dependent priors. In this sense, deep linear networks make provably optimal predictions. We also prove that, starting from data-agnostic priors, Bayesian model evidence in wide networks is only maximized at infinite depth. This gives a principled reason to prefer deeper networks (at least in the linear case). Finally, our results show that with data-agnostic priors a novel notion of effective depth given by \[\#\text{hidden layers}\times\frac{\#\text{training data}}{\text{network width}}\] determines the Bayesian posterior in wide linear networks, giving rigorous new scaling laws for generalization error.

Biological error correction codes generate fault-tolerant neural networks

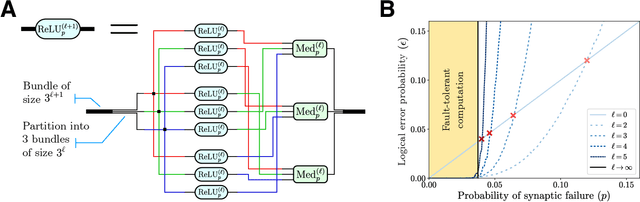
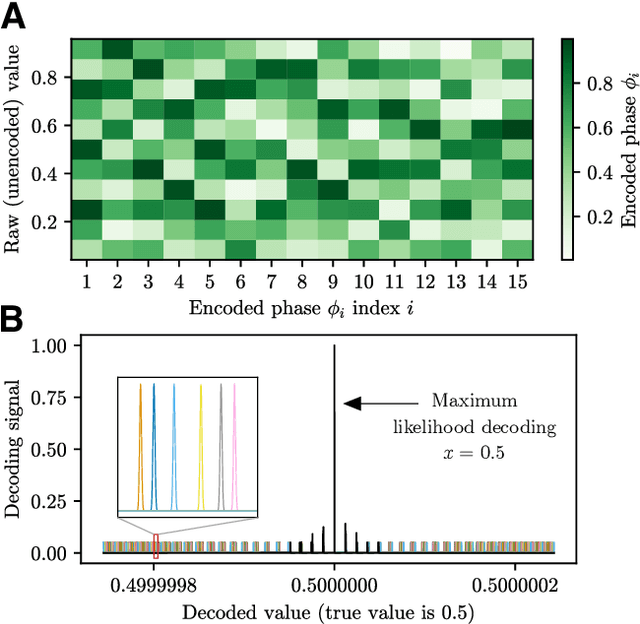
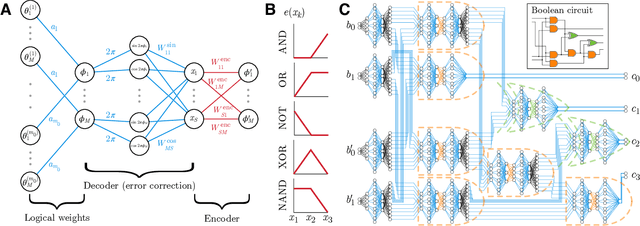
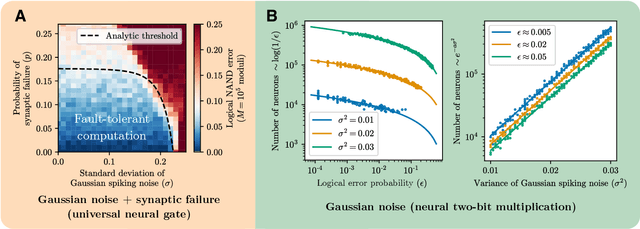
It has been an open question in deep learning if fault-tolerant computation is possible: can arbitrarily reliable computation be achieved using only unreliable neurons? In the mammalian cortex, analog error correction codes known as grid codes have been observed to protect states against neural spiking noise, but their role in information processing is unclear. Here, we use these biological codes to show that a universal fault-tolerant neural network can be achieved if the faultiness of each neuron lies below a sharp threshold, which we find coincides in order of magnitude with noise observed in biological neurons. The discovery of a sharp phase transition from faulty to fault-tolerant neural computation opens a path towards understanding noisy analog systems in artificial intelligence and neuroscience.

A quantum algorithm for training wide and deep classical neural networks

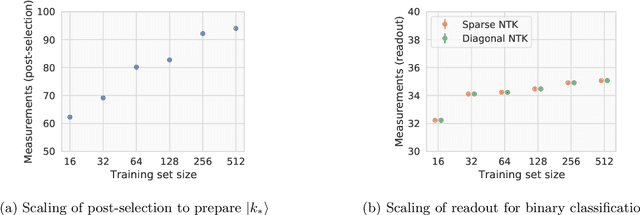
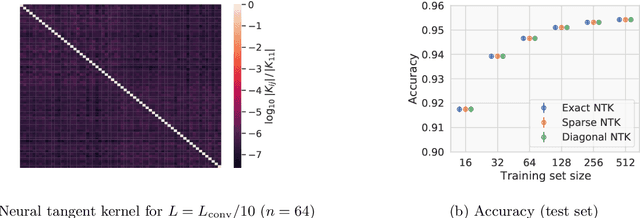
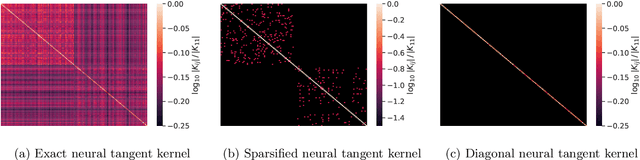
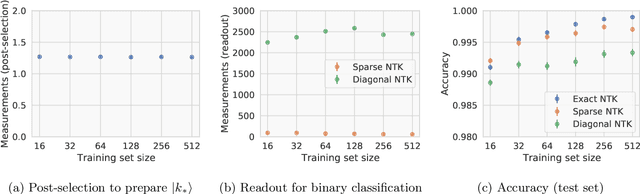
Given the success of deep learning in classical machine learning, quantum algorithms for traditional neural network architectures may provide one of the most promising settings for quantum machine learning. Considering a fully-connected feedforward neural network, we show that conditions amenable to classical trainability via gradient descent coincide with those necessary for efficiently solving quantum linear systems. We propose a quantum algorithm to approximately train a wide and deep neural network up to $O(1/n)$ error for a training set of size $n$ by performing sparse matrix inversion in $O(\log n)$ time. To achieve an end-to-end exponential speedup over gradient descent, the data distribution must permit efficient state preparation and readout. We numerically demonstrate that the MNIST image dataset satisfies such conditions; moreover, the quantum algorithm matches the accuracy of the fully-connected network. Beyond the proven architecture, we provide empirical evidence for $O(\log n)$ training of a convolutional neural network with pooling.

Quantum adiabatic machine learning with zooming

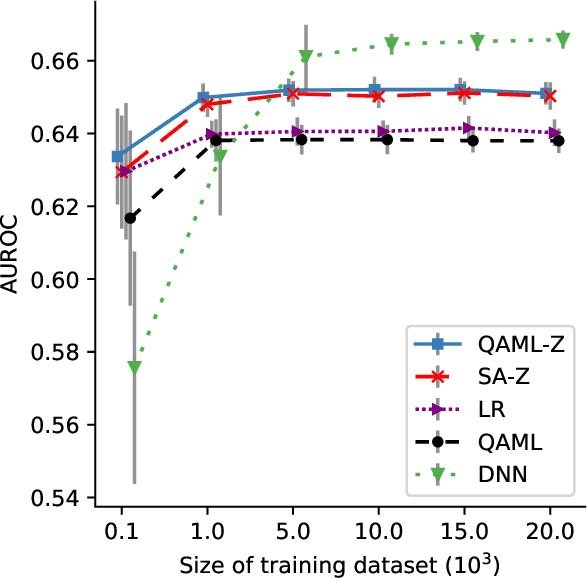
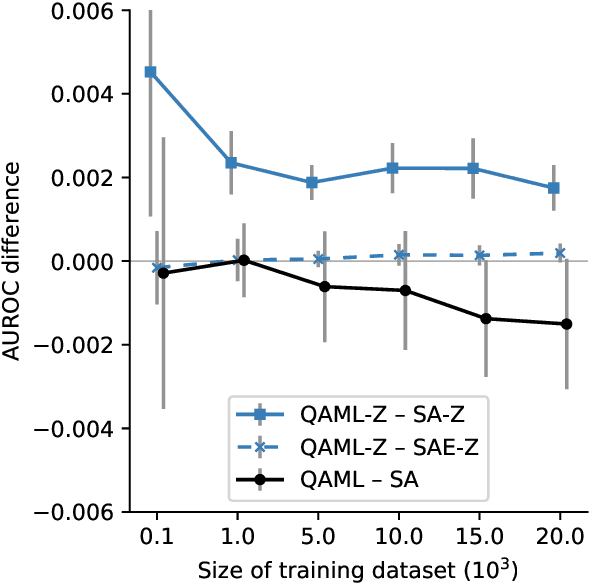
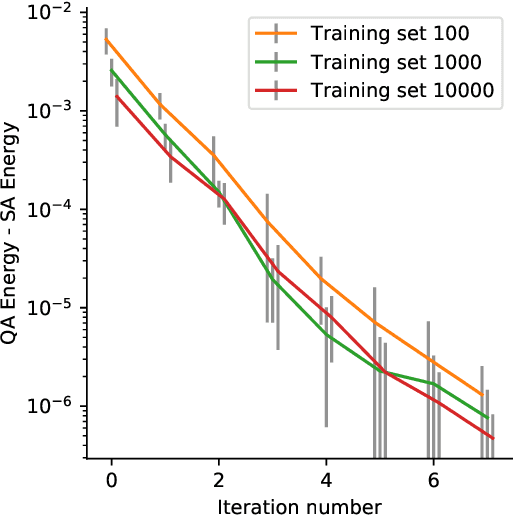
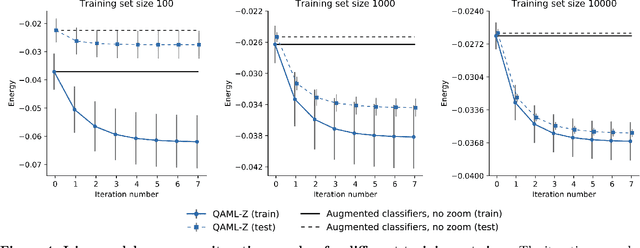
Recent work has shown that quantum annealing for machine learning (QAML) can perform comparably to state-of-the-art machine learning methods with a specific application to Higgs boson classification. We propose a variant algorithm (QAML-Z) that iteratively zooms in on a region of the energy surface by mapping the problem to a continuous space and sequentially applying quantum annealing to an augmented set of weak classifiers. Results on a programmable quantum annealer show that QAML-Z increases the performance difference between QAML and classical deep neural networks by over 40% as measured by area under the ROC curve for small training set sizes. Furthermore, QAML-Z reduces the advantage of deep neural networks over QAML for large training sets by around 50%, indicating that QAML-Z produces stronger classifiers that retain the robustness of the original QAML algorithm.

Charged particle tracking with quantum annealing-inspired optimization

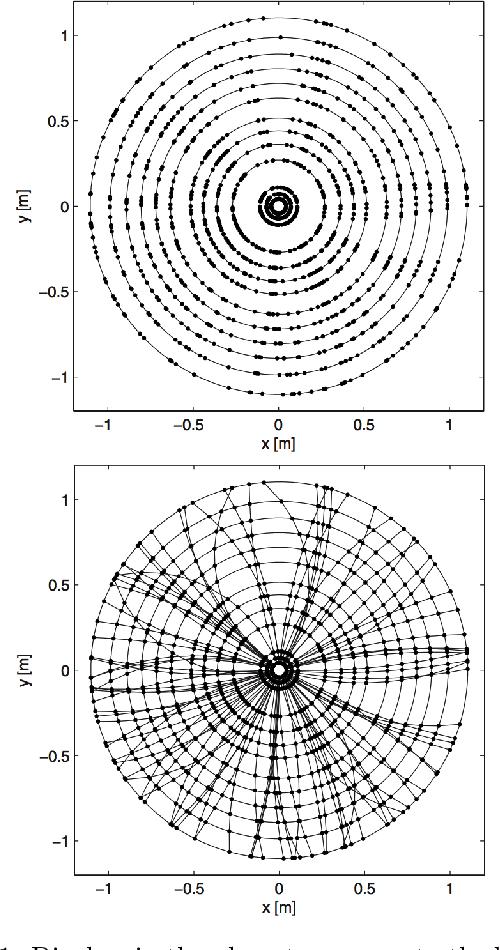
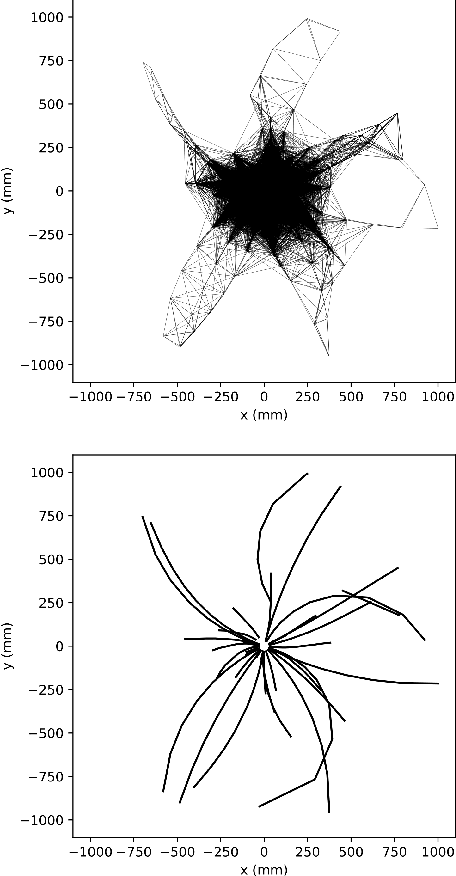
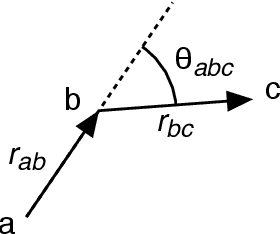
At the High Luminosity Large Hadron Collider (HL-LHC), traditional track reconstruction techniques that are critical for analysis are expected to face challenges due to scaling with track density. Quantum annealing has shown promise in its ability to solve combinatorial optimization problems amidst an ongoing effort to establish evidence of a quantum speedup. As a step towards exploiting such potential speedup, we investigate a track reconstruction approach by adapting the existing geometric Denby-Peterson (Hopfield) network method to the quantum annealing framework and to HL-LHC conditions. Furthermore, we develop additional techniques to embed the problem onto existing and near-term quantum annealing hardware. Results using simulated annealing and quantum annealing with the D-Wave 2X system on the TrackML dataset are presented, demonstrating the successful application of a quantum annealing-inspired algorithm to the track reconstruction challenge. We find that combinatorial optimization problems can effectively reconstruct tracks, suggesting possible applications for fast hardware-specific implementations at the LHC while leaving open the possibility of a quantum speedup for tracking.