A Comparative Study of Modern Inference Techniques for Structured Discrete Energy Minimization Problems

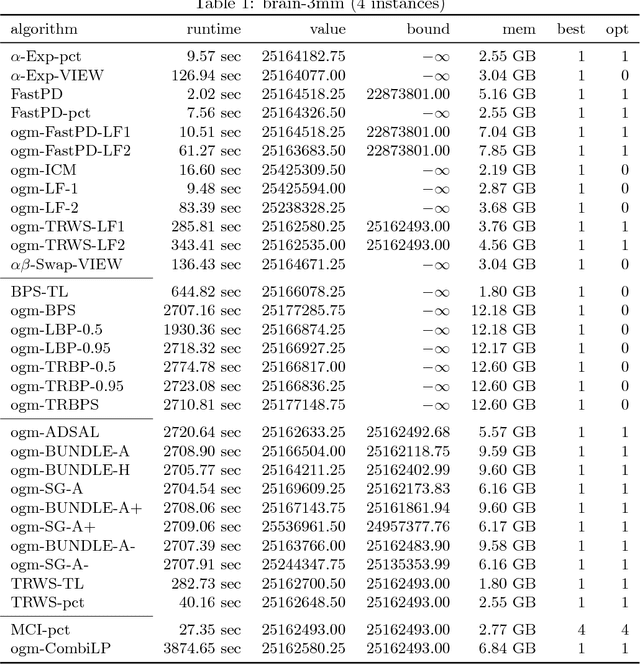
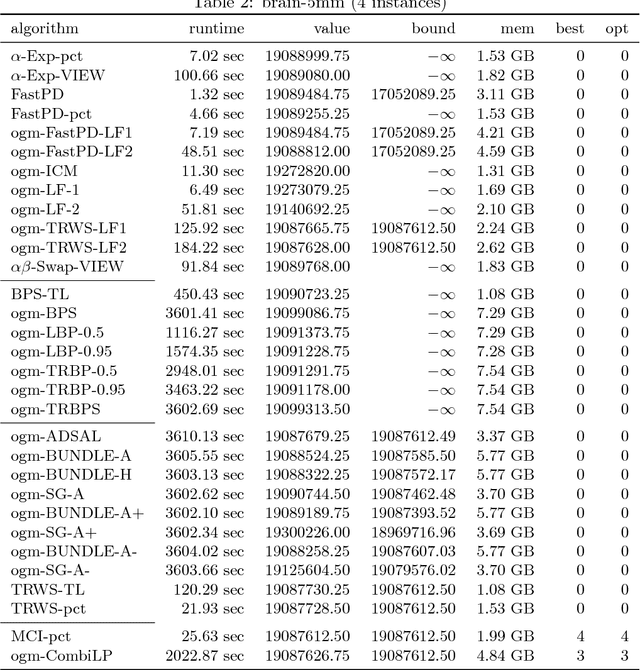
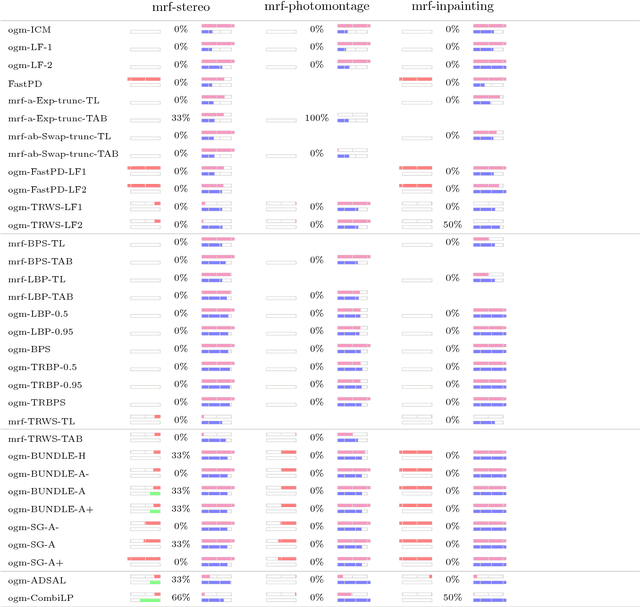
Szeliski et al. published an influential study in 2006 on energy minimization methods for Markov Random Fields (MRF). This study provided valuable insights in choosing the best optimization technique for certain classes of problems. While these insights remain generally useful today, the phenomenal success of random field models means that the kinds of inference problems that have to be solved changed significantly. Specifically, the models today often include higher order interactions, flexible connectivity structures, large la\-bel-spaces of different cardinalities, or learned energy tables. To reflect these changes, we provide a modernized and enlarged study. We present an empirical comparison of 32 state-of-the-art optimization techniques on a corpus of 2,453 energy minimization instances from diverse applications in computer vision. To ensure reproducibility, we evaluate all methods in the OpenGM 2 framework and report extensive results regarding runtime and solution quality. Key insights from our study agree with the results of Szeliski et al. for the types of models they studied. However, on new and challenging types of models our findings disagree and suggest that polyhedral methods and integer programming solvers are competitive in terms of runtime and solution quality over a large range of model types.

Efficient MRF Energy Minimization via Adaptive Diminishing Smoothing

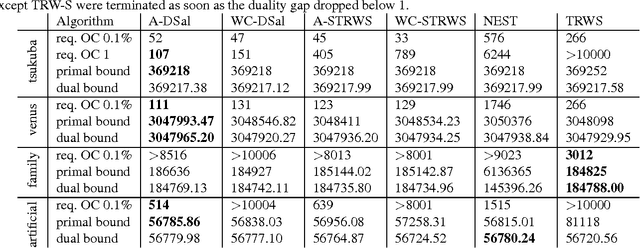
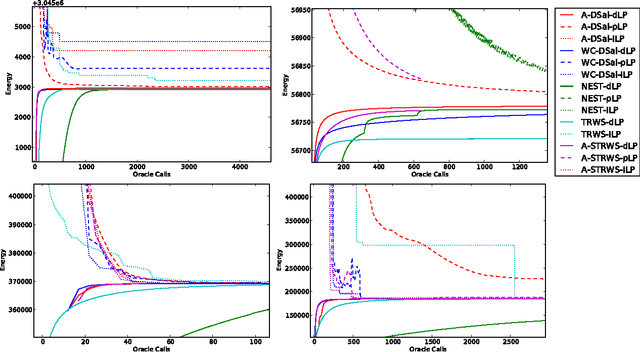
We consider the linear programming relaxation of an energy minimization problem for Markov Random Fields. The dual objective of this problem can be treated as a concave and unconstrained, but non-smooth function. The idea of smoothing the objective prior to optimization was recently proposed in a series of papers. Some of them suggested the idea to decrease the amount of smoothing (so called temperature) while getting closer to the optimum. However, no theoretical substantiation was provided. We propose an adaptive smoothing diminishing algorithm based on the duality gap between relaxed primal and dual objectives and demonstrate the efficiency of our approach with a smoothed version of Sequential Tree-Reweighted Message Passing (TRW-S) algorithm. The strategy is applicable to other algorithms as well, avoids adhoc tuning of the smoothing during iterations, and provably guarantees convergence to the optimum.

Getting Feasible Variable Estimates From Infeasible Ones: MRF Local Polytope Study

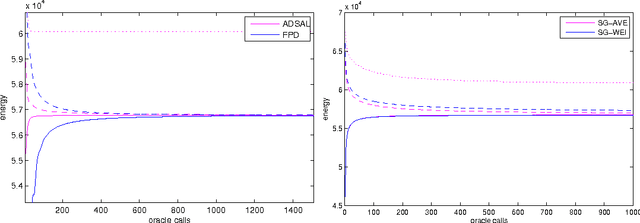
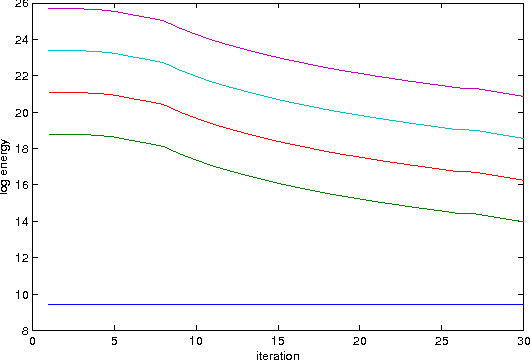
This paper proposes a method for construction of approximate feasible primal solutions from dual ones for large-scale optimization problems possessing certain separability properties. Whereas infeasible primal estimates can typically be produced from (sub-)gradients of the dual function, it is often not easy to project them to the primal feasible set, since the projection itself has a complexity comparable to the complexity of the initial problem. We propose an alternative efficient method to obtain feasibility and show that its properties influencing the convergence to the optimum are similar to the properties of the Euclidean projection. We apply our method to the local polytope relaxation of inference problems for Markov Random Fields and demonstrate its superiority over existing methods.