Discrete graphical models -- an optimization perspective

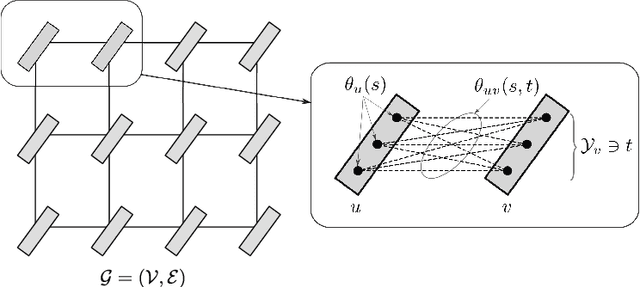
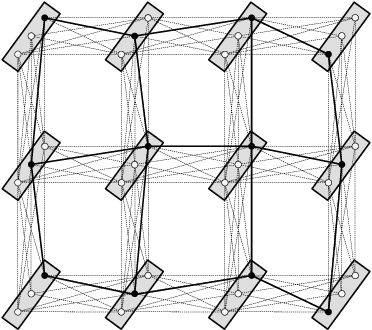
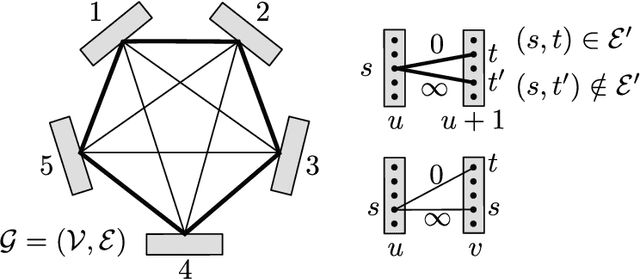
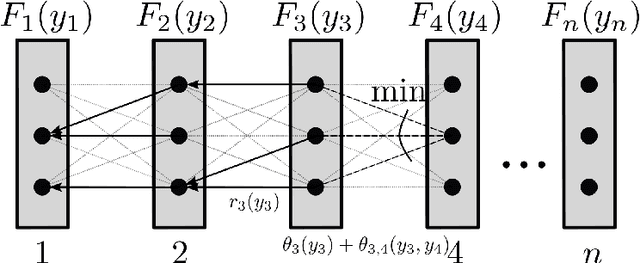
This monograph is about discrete energy minimization for discrete graphical models. It considers graphical models, or, more precisely, maximum a posteriori inference for graphical models, purely as a combinatorial optimization problem. Modeling, applications, probabilistic interpretations and many other aspects are either ignored here or find their place in examples and remarks only. It covers the integer linear programming formulation of the problem as well as its linear programming, Lagrange and Lagrange decomposition-based relaxations. In particular, it provides a detailed analysis of the polynomially solvable acyclic and submodular problems, along with the corresponding exact optimization methods. Major approximate methods, such as message passing and graph cut techniques are also described and analyzed comprehensively. The monograph can be useful for undergraduate and graduate students studying optimization or graphical models, as well as for experts in optimization who want to have a look into graphical models. To make the monograph suitable for both categories of readers we explicitly separate the mathematical optimization background chapters from those specific to graphical models.

Maximum Persistency via Iterative Relaxed Inference with Graphical Models

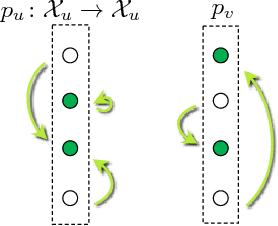
We consider the NP-hard problem of MAP-inference for undirected discrete graphical models. We propose a polynomial time and practically efficient algorithm for finding a part of its optimal solution. Specifically, our algorithm marks some labels of the considered graphical model either as (i) optimal, meaning that they belong to all optimal solutions of the inference problem; (ii) non-optimal if they provably do not belong to any solution. With access to an exact solver of a linear programming relaxation to the MAP-inference problem, our algorithm marks the maximal possible (in a specified sense) number of labels. We also present a version of the algorithm, which has access to a suboptimal dual solver only and still can ensure the (non-)optimality for the marked labels, although the overall number of the marked labels may decrease. We propose an efficient implementation, which runs in time comparable to a single run of a suboptimal dual solver. Our method is well-scalable and shows state-of-the-art results on computational benchmarks from machine learning and computer vision.

A Dual Ascent Framework for Lagrangean Decomposition of Combinatorial Problems

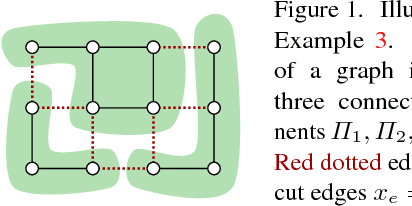
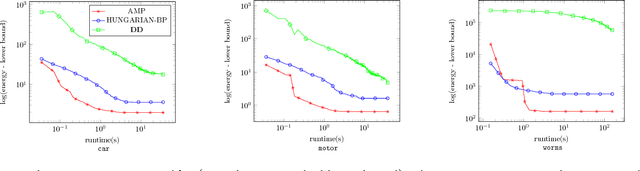
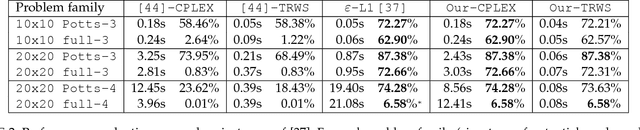
We propose a general dual ascent framework for Lagrangean decomposition of combinatorial problems. Although methods of this type have shown their efficiency for a number of problems, so far there was no general algorithm applicable to multiple problem types. In his work, we propose such a general algorithm. It depends on several parameters, which can be used to optimize its performance in each particular setting. We demonstrate efficacy of our method on graph matching and multicut problems, where it outperforms state-of-the-art solvers including those based on subgradient optimization and off-the-shelf linear programming solvers.

A Study of Lagrangean Decompositions and Dual Ascent Solvers for Graph Matching

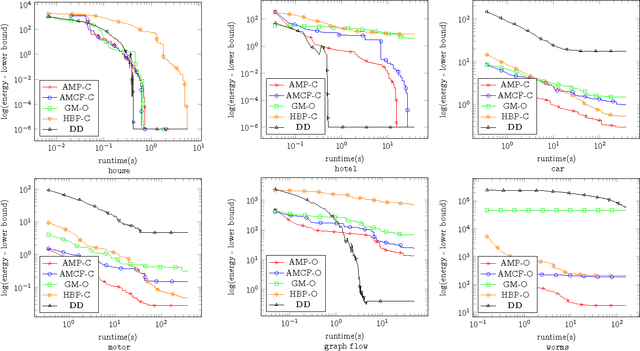
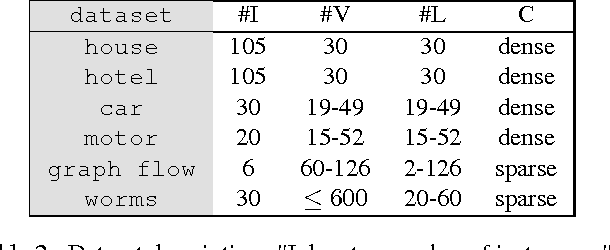
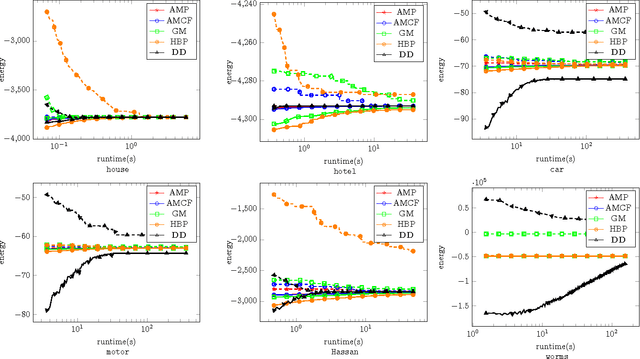
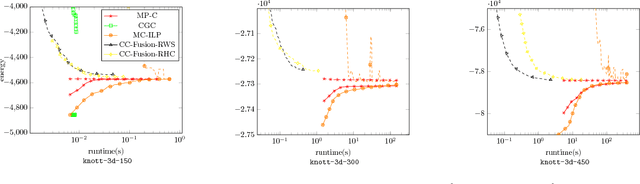
We study the quadratic assignment problem, in computer vision also known as graph matching. Two leading solvers for this problem optimize the Lagrange decomposition duals with sub-gradient and dual ascent (also known as message passing) updates. We explore s direction further and propose several additional Lagrangean relaxations of the graph matching problem along with corresponding algorithms, which are all based on a common dual ascent framework. Our extensive empirical evaluation gives several theoretical insights and suggests a new state-of-the-art any-time solver for the considered problem. Our improvement over state-of-the-art is particularly visible on a new dataset with large-scale sparse problem instances containing more than 500 graph nodes each.

Global Hypothesis Generation for 6D Object Pose Estimation

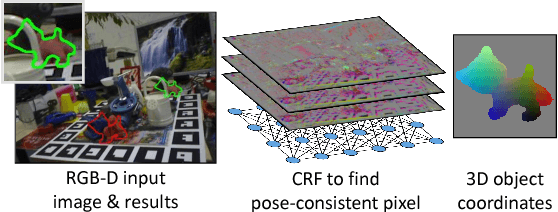
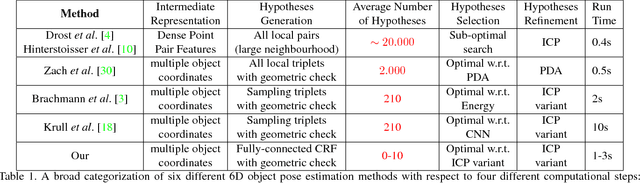
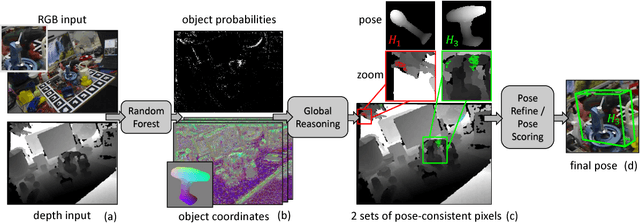
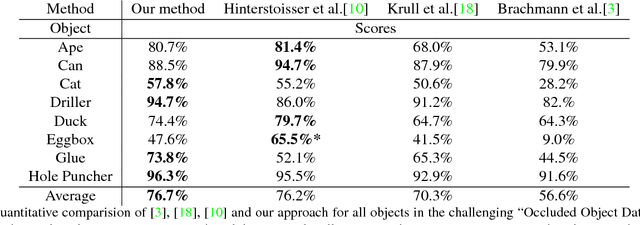
This paper addresses the task of estimating the 6D pose of a known 3D object from a single RGB-D image. Most modern approaches solve this task in three steps: i) Compute local features; ii) Generate a pool of pose-hypotheses; iii) Select and refine a pose from the pool. This work focuses on the second step. While all existing approaches generate the hypotheses pool via local reasoning, e.g. RANSAC or Hough-voting, we are the first to show that global reasoning is beneficial at this stage. In particular, we formulate a novel fully-connected Conditional Random Field (CRF) that outputs a very small number of pose-hypotheses. Despite the potential functions of the CRF being non-Gaussian, we give a new and efficient two-step optimization procedure, with some guarantees for optimality. We utilize our global hypotheses generation procedure to produce results that exceed state-of-the-art for the challenging "Occluded Object Dataset".

InstanceCut: from Edges to Instances with MultiCut

This work addresses the task of instance-aware semantic segmentation. Our key motivation is to design a simple method with a new modelling-paradigm, which therefore has a different trade-off between advantages and disadvantages compared to known approaches. Our approach, we term InstanceCut, represents the problem by two output modalities: (i) an instance-agnostic semantic segmentation and (ii) all instance-boundaries. The former is computed from a standard convolutional neural network for semantic segmentation, and the latter is derived from a new instance-aware edge detection model. To reason globally about the optimal partitioning of an image into instances, we combine these two modalities into a novel MultiCut formulation. We evaluate our approach on the challenging CityScapes dataset. Despite the conceptual simplicity of our approach, we achieve the best result among all published methods, and perform particularly well for rare object classes.

Joint Training of Generic CNN-CRF Models with Stochastic Optimization

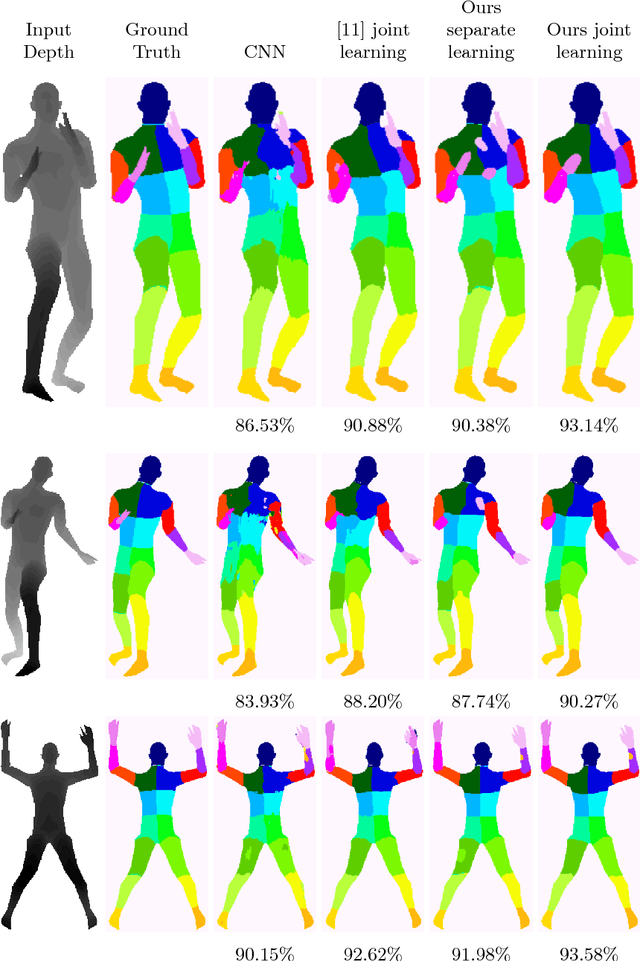
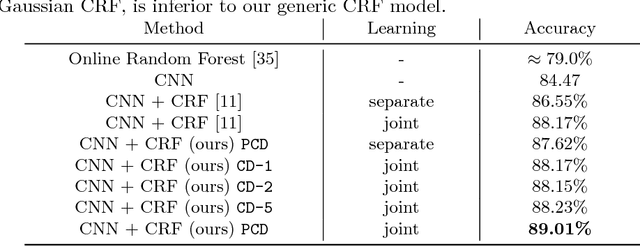
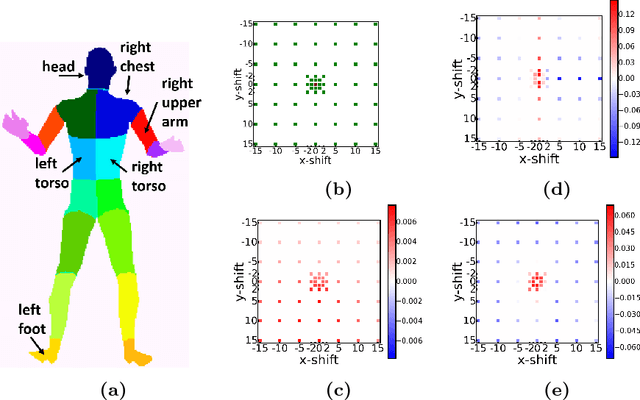
We propose a new CNN-CRF end-to-end learning framework, which is based on joint stochastic optimization with respect to both Convolutional Neural Network (CNN) and Conditional Random Field (CRF) parameters. While stochastic gradient descent is a standard technique for CNN training, it was not used for joint models so far. We show that our learning method is (i) general, i.e. it applies to arbitrary CNN and CRF architectures and potential functions; (ii) scalable, i.e. it has a low memory footprint and straightforwardly parallelizes on GPUs; (iii) easy in implementation. Additionally, the unified CNN-CRF optimization approach simplifies a potential hardware implementation. We empirically evaluate our method on the task of semantic labeling of body parts in depth images and show that it compares favorably to competing techniques.

Joint M-Best-Diverse Labelings as a Parametric Submodular Minimization

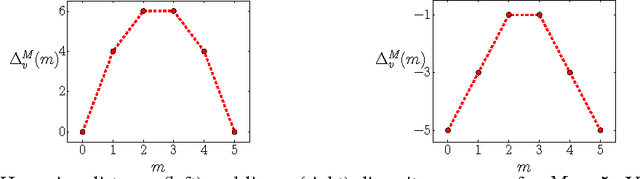
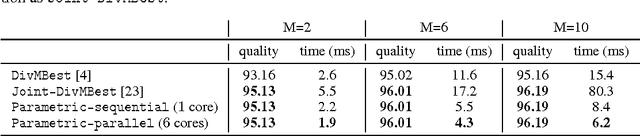
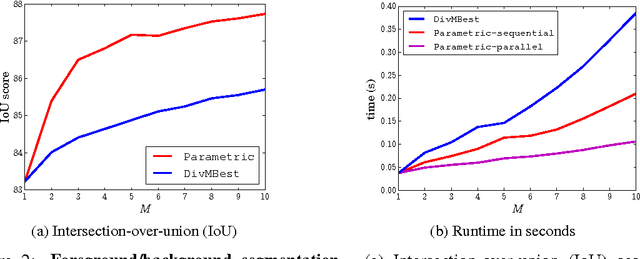
We consider the problem of jointly inferring the M-best diverse labelings for a binary (high-order) submodular energy of a graphical model. Recently, it was shown that this problem can be solved to a global optimum, for many practically interesting diversity measures. It was noted that the labelings are, so-called, nested. This nestedness property also holds for labelings of a class of parametric submodular minimization problems, where different values of the global parameter $\gamma$ give rise to different solutions. The popular example of the parametric submodular minimization is the monotonic parametric max-flow problem, which is also widely used for computing multiple labelings. As the main contribution of this work we establish a close relationship between diversity with submodular energies and the parametric submodular minimization. In particular, the joint M-best diverse labelings can be obtained by running a non-parametric submodular minimization (in the special case - max-flow) solver for M different values of $\gamma$ in parallel, for certain diversity measures. Importantly, the values for $\gamma$ can be computed in a closed form in advance, prior to any optimization. These theoretical results suggest two simple yet efficient algorithms for the joint M-best diverse problem, which outperform competitors in terms of runtime and quality of results. In particular, as we show in the paper, the new methods compute the exact M-best diverse labelings faster than a popular method of Batra et al., which in some sense only obtains approximate solutions.

Multicuts and Perturb & MAP for Probabilistic Graph Clustering

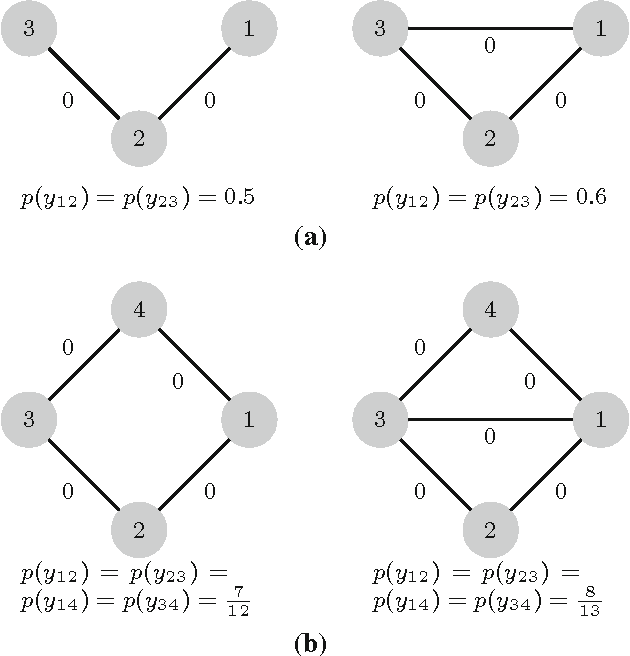
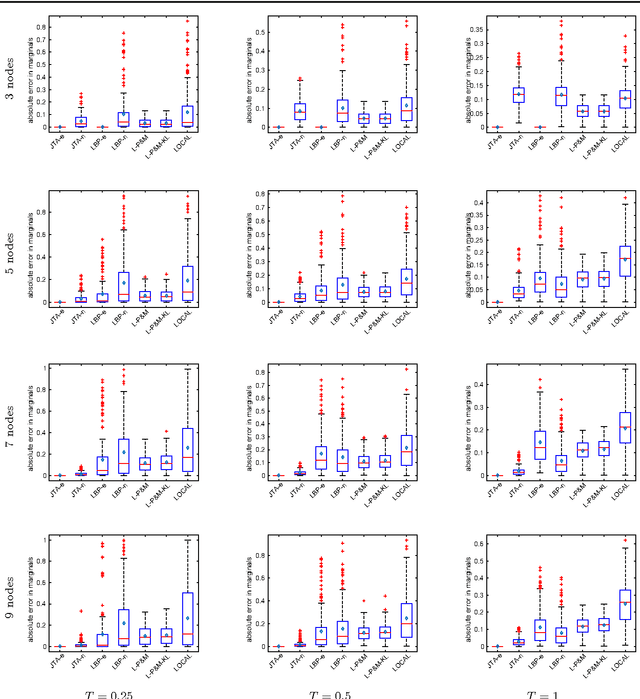
We present a probabilistic graphical model formulation for the graph clustering problem. This enables to locally represent uncertainty of image partitions by approximate marginal distributions in a mathematically substantiated way, and to rectify local data term cues so as to close contours and to obtain valid partitions. We exploit recent progress on globally optimal MAP inference by integer programming and on perturbation-based approximations of the log-partition function, in order to sample clusterings and to estimate marginal distributions of node-pairs both more accurately and more efficiently than state-of-the-art methods. Our approach works for any graphically represented problem instance. This is demonstrated for image segmentation and social network cluster analysis. Our mathematical ansatz should be relevant also for other combinatorial problems.

Partial Optimality by Pruning for MAP-Inference with General Graphical Models

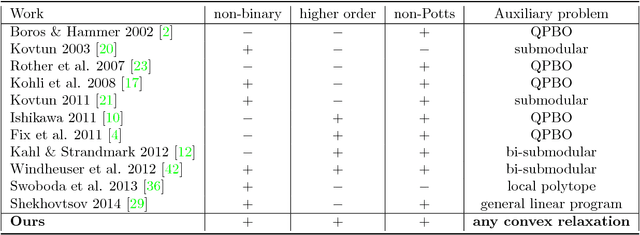
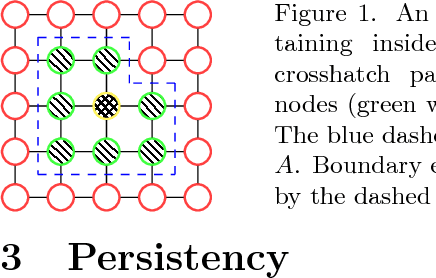
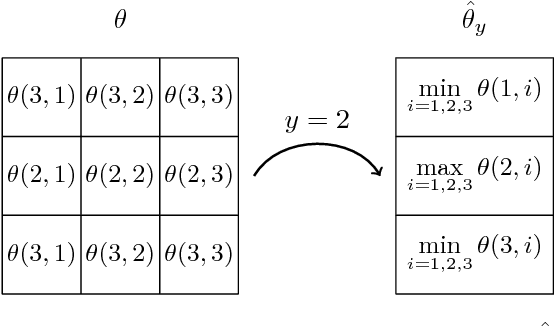
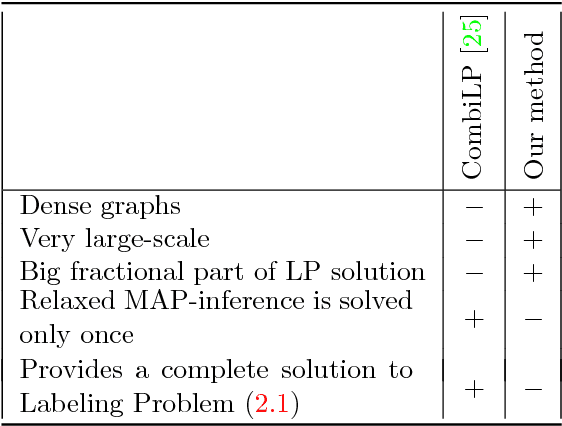
We consider the energy minimization problem for undirected graphical models, also known as MAP-inference problem for Markov random fields which is NP-hard in general. We propose a novel polynomial time algorithm to obtain a part of its optimal non-relaxed integral solution. Our algorithm is initialized with variables taking integral values in the solution of a convex relaxation of the MAP-inference problem and iteratively prunes those, which do not satisfy our criterion for partial optimality. We show that our pruning strategy is in a certain sense theoretically optimal. Also empirically our method outperforms previous approaches in terms of the number of persistently labelled variables. The method is very general, as it is applicable to models with arbitrary factors of an arbitrary order and can employ any solver for the considered relaxed problem. Our method's runtime is determined by the runtime of the convex relaxation solver for the MAP-inference problem.