Multicuts and Perturb & MAP for Probabilistic Graph Clustering

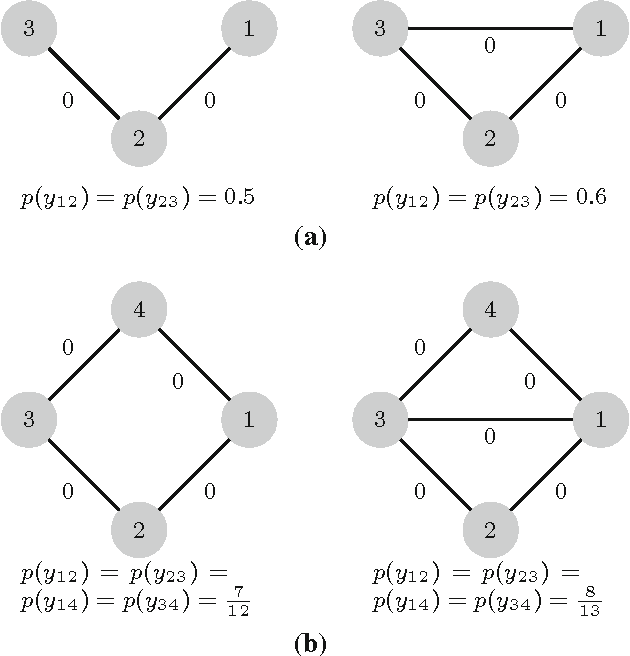
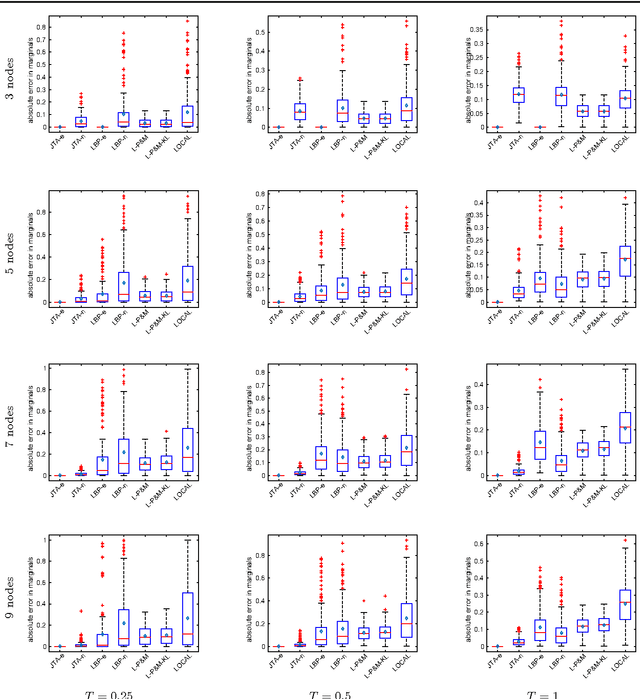
We present a probabilistic graphical model formulation for the graph clustering problem. This enables to locally represent uncertainty of image partitions by approximate marginal distributions in a mathematically substantiated way, and to rectify local data term cues so as to close contours and to obtain valid partitions. We exploit recent progress on globally optimal MAP inference by integer programming and on perturbation-based approximations of the log-partition function, in order to sample clusterings and to estimate marginal distributions of node-pairs both more accurately and more efficiently than state-of-the-art methods. Our approach works for any graphically represented problem instance. This is demonstrated for image segmentation and social network cluster analysis. Our mathematical ansatz should be relevant also for other combinatorial problems.

Partial Optimality by Pruning for MAP-Inference with General Graphical Models

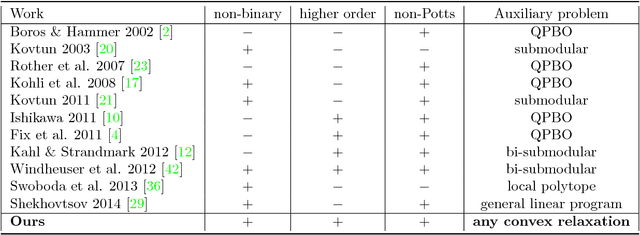
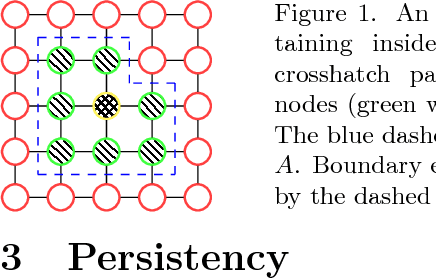
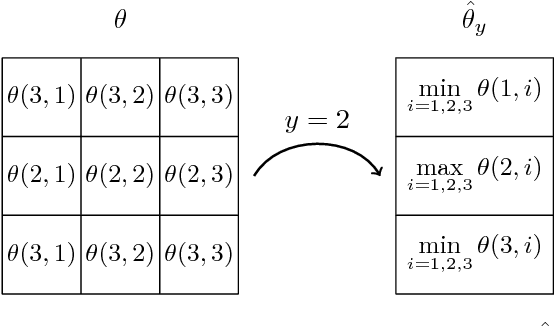
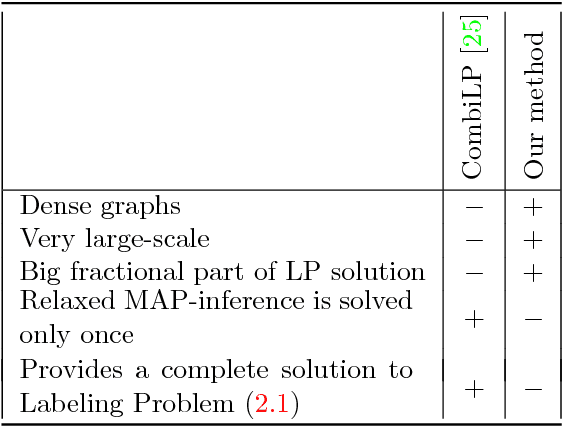
We consider the energy minimization problem for undirected graphical models, also known as MAP-inference problem for Markov random fields which is NP-hard in general. We propose a novel polynomial time algorithm to obtain a part of its optimal non-relaxed integral solution. Our algorithm is initialized with variables taking integral values in the solution of a convex relaxation of the MAP-inference problem and iteratively prunes those, which do not satisfy our criterion for partial optimality. We show that our pruning strategy is in a certain sense theoretically optimal. Also empirically our method outperforms previous approaches in terms of the number of persistently labelled variables. The method is very general, as it is applicable to models with arbitrary factors of an arbitrary order and can employ any solver for the considered relaxed problem. Our method's runtime is determined by the runtime of the convex relaxation solver for the MAP-inference problem.