Efficient kernelized bandit algorithms via exploration distributions

We consider a kernelized bandit problem with a compact arm set ${X} \subset \mathbb{R}^d $ and a fixed but unknown reward function $f^*$ with a finite norm in some Reproducing Kernel Hilbert Space (RKHS). We propose a class of computationally efficient kernelized bandit algorithms, which we call GP-Generic, based on a novel concept: exploration distributions. This class of algorithms includes Upper Confidence Bound-based approaches as a special case, but also allows for a variety of randomized algorithms. With careful choice of exploration distribution, our proposed generic algorithm realizes a wide range of concrete algorithms that achieve $\tilde{O}(\gamma_T\sqrt{T})$ regret bounds, where $\gamma_T$ characterizes the RKHS complexity. This matches known results for UCB- and Thompson Sampling-based algorithms; we also show that in practice, randomization can yield better practical results.

Connecting Thompson Sampling and UCB: Towards More Efficient Trade-offs Between Privacy and Regret

We address differentially private stochastic bandit problems from the angles of exploring the deep connections among Thompson Sampling with Gaussian priors, Gaussian mechanisms, and Gaussian differential privacy (GDP). We propose DP-TS-UCB, a novel parametrized private bandit algorithm that enables to trade off privacy and regret. DP-TS-UCB satisfies $ \tilde{O} \left(T^{0.25(1-\alpha)}\right)$-GDP and enjoys an $O \left(K\ln^{\alpha+1}(T)/\Delta \right)$ regret bound, where $\alpha \in [0,1]$ controls the trade-off between privacy and regret. Theoretically, our DP-TS-UCB relies on anti-concentration bounds of Gaussian distributions and links exploration mechanisms in Thompson Sampling-based algorithms and Upper Confidence Bound-based algorithms, which may be of independent interest.

Efficient and Adaptive Posterior Sampling Algorithms for Bandits

We study Thompson Sampling-based algorithms for stochastic bandits with bounded rewards. As the existing problem-dependent regret bound for Thompson Sampling with Gaussian priors [Agrawal and Goyal, 2017] is vacuous when $T \le 288 e^{64}$, we derive a more practical bound that tightens the coefficient of the leading term %from $288 e^{64}$ to $1270$. Additionally, motivated by large-scale real-world applications that require scalability, adaptive computational resource allocation, and a balance in utility and computation, we propose two parameterized Thompson Sampling-based algorithms: Thompson Sampling with Model Aggregation (TS-MA-$\alpha$) and Thompson Sampling with Timestamp Duelling (TS-TD-$\alpha$), where $\alpha \in [0,1]$ controls the trade-off between utility and computation. Both algorithms achieve $O \left(K\ln^{\alpha+1}(T)/\Delta \right)$ regret bound, where $K$ is the number of arms, $T$ is the finite learning horizon, and $\Delta$ denotes the single round performance loss when pulling a sub-optimal arm.

Optimal Algorithms for Private Online Learning in a Stochastic Environment

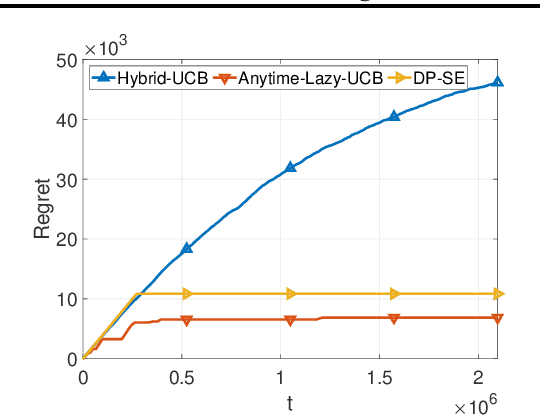
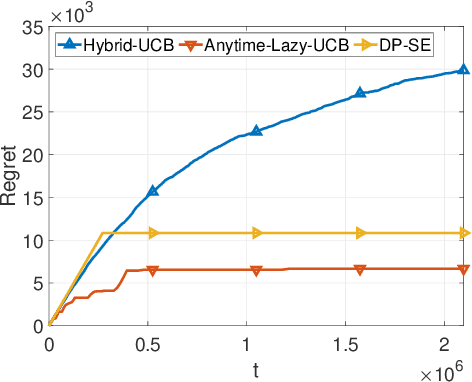
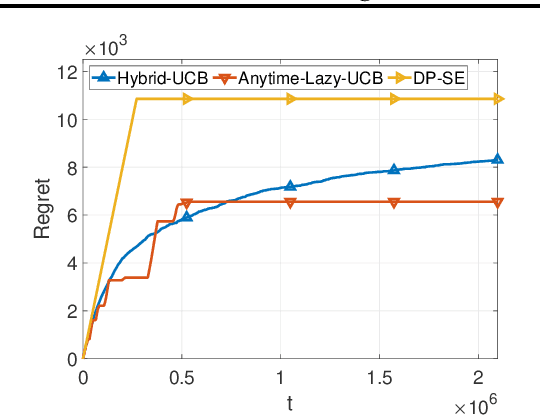
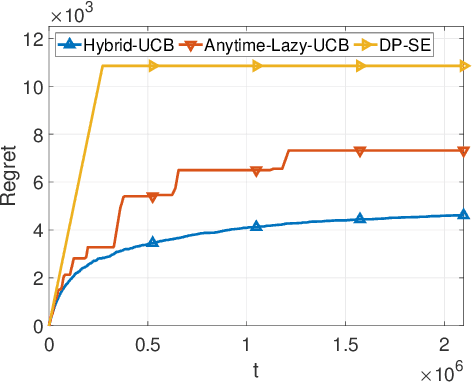
We consider two variants of private stochastic online learning. The first variant is differentially private stochastic bandits. Previously, Sajed and Sheffet (2019) devised the DP Successive Elimination (DP-SE) algorithm that achieves the optimal $ O \biggl(\sum\limits_{1\le j \le K: \Delta_j >0} \frac{ \log T}{ \Delta_j} + \frac{ K\log T}{\epsilon} \biggr)$ problem-dependent regret bound, where $K$ is the number of arms, $\Delta_j$ is the mean reward gap of arm $j$, $T$ is the time horizon, and $\epsilon$ is the required privacy parameter. However, like other elimination style algorithms, it is not an anytime algorithm. Until now, it was not known whether UCB-based algorithms could achieve this optimal regret bound. We present an anytime, UCB-based algorithm that achieves optimality. Our experiments show that the UCB-based algorithm is competitive with DP-SE. The second variant is the full information version of private stochastic online learning. Specifically, for the problems of decision-theoretic online learning with stochastic rewards, we present the first algorithm that achieves an $ O \left( \frac{ \log K}{ \Delta_{\min}} + \frac{ \log K}{\epsilon} \right)$ regret bound, where $\Delta_{\min}$ is the minimum mean reward gap. The key idea behind our good theoretical guarantees in both settings is the forgetfulness, i.e., decisions are made based on a certain amount of newly obtained observations instead of all the observations obtained from the very beginning.

Thompson Sampling for Combinatorial Semi-bandits with Sleeping Arms and Long-Term Fairness Constraints

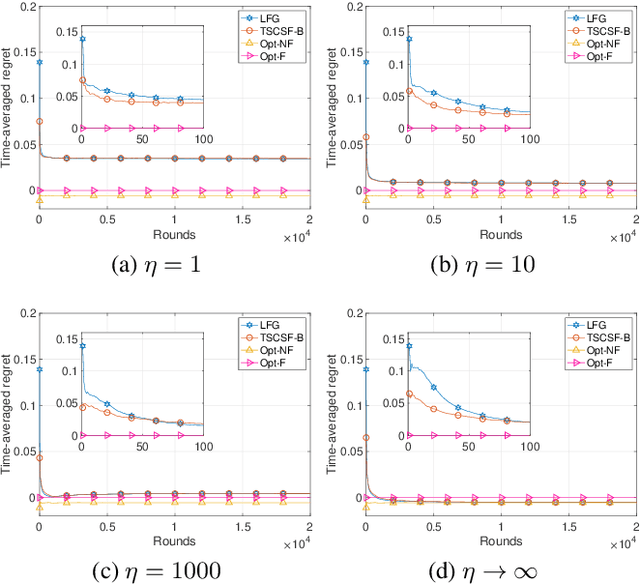
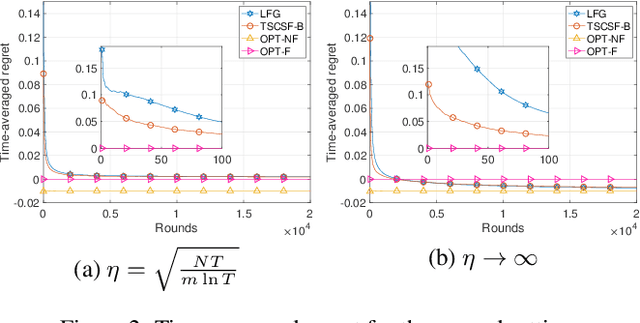
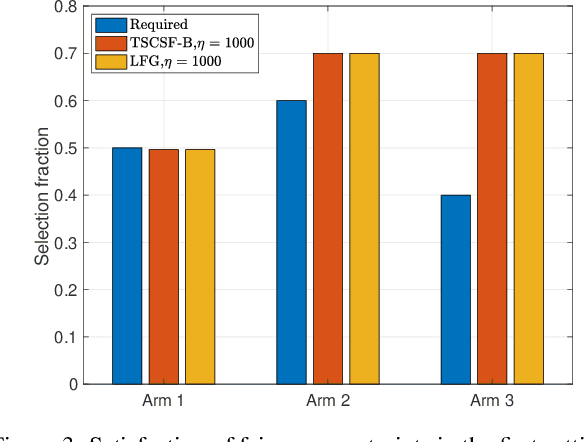
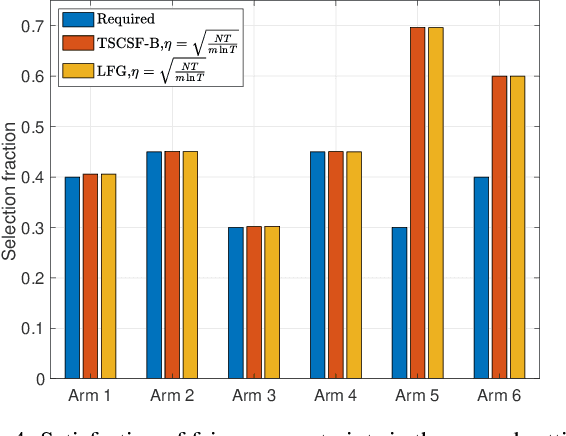
We study the combinatorial sleeping multi-armed semi-bandit problem with long-term fairness constraints~(CSMAB-F). To address the problem, we adopt Thompson Sampling~(TS) to maximize the total rewards and use virtual queue techniques to handle the fairness constraints, and design an algorithm called \emph{TS with beta priors and Bernoulli likelihoods for CSMAB-F~(TSCSF-B)}. Further, we prove TSCSF-B can satisfy the fairness constraints, and the time-averaged regret is upper bounded by $\frac{N}{2\eta} + O\left(\frac{\sqrt{mNT\ln T}}{T}\right)$, where $N$ is the total number of arms, $m$ is the maximum number of arms that can be pulled simultaneously in each round~(the cardinality constraint) and $\eta$ is the parameter trading off fairness for rewards. By relaxing the fairness constraints (i.e., let $\eta \rightarrow \infty$), the bound boils down to the first problem-independent bound of TS algorithms for combinatorial sleeping multi-armed semi-bandit problems. Finally, we perform numerical experiments and use a high-rating movie recommendation application to show the effectiveness and efficiency of the proposed algorithm.