Thompson Sampling for Combinatorial Semi-bandits with Sleeping Arms and Long-Term Fairness Constraints
Paper and Code
May 14, 2020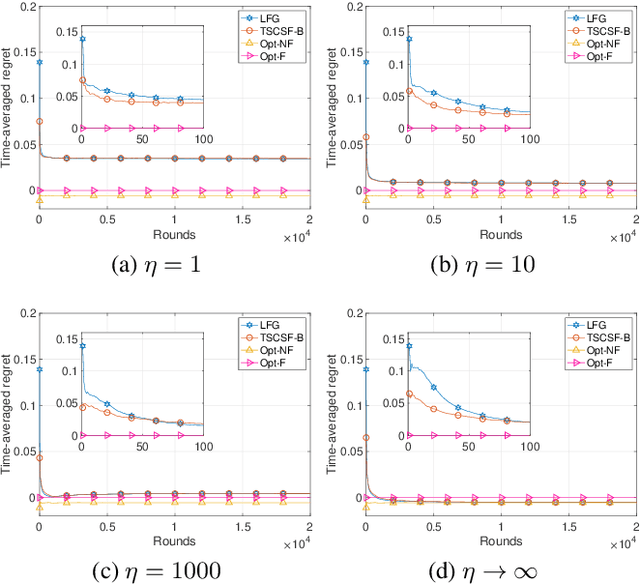
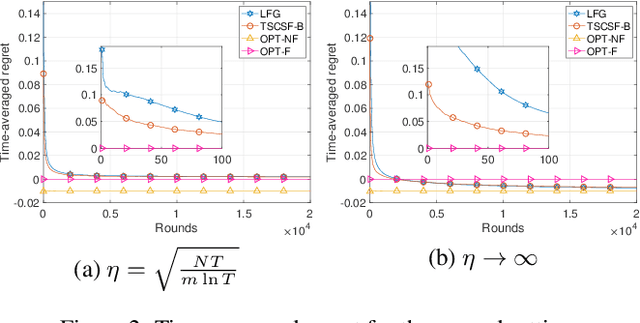
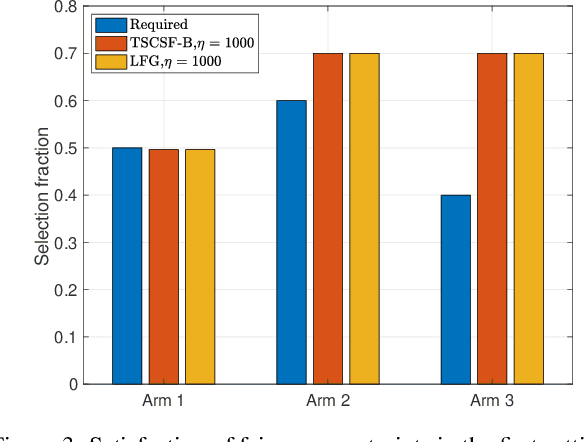
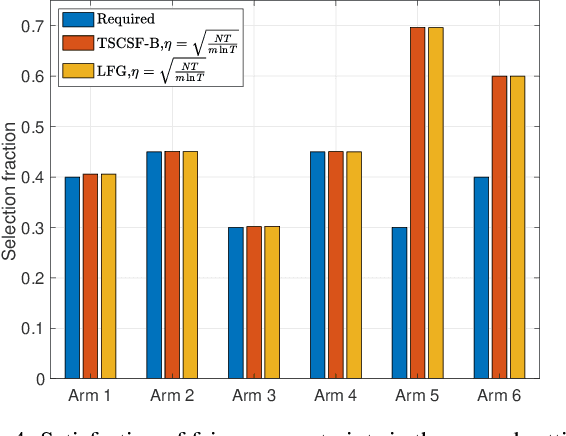
We study the combinatorial sleeping multi-armed semi-bandit problem with long-term fairness constraints~(CSMAB-F). To address the problem, we adopt Thompson Sampling~(TS) to maximize the total rewards and use virtual queue techniques to handle the fairness constraints, and design an algorithm called \emph{TS with beta priors and Bernoulli likelihoods for CSMAB-F~(TSCSF-B)}. Further, we prove TSCSF-B can satisfy the fairness constraints, and the time-averaged regret is upper bounded by $\frac{N}{2\eta} + O\left(\frac{\sqrt{mNT\ln T}}{T}\right)$, where $N$ is the total number of arms, $m$ is the maximum number of arms that can be pulled simultaneously in each round~(the cardinality constraint) and $\eta$ is the parameter trading off fairness for rewards. By relaxing the fairness constraints (i.e., let $\eta \rightarrow \infty$), the bound boils down to the first problem-independent bound of TS algorithms for combinatorial sleeping multi-armed semi-bandit problems. Finally, we perform numerical experiments and use a high-rating movie recommendation application to show the effectiveness and efficiency of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge