FinTRec: Transformer Based Unified Contextual Ads Targeting and Personalization for Financial Applications

Transformer-based architectures are widely adopted in sequential recommendation systems, yet their application in Financial Services (FS) presents distinct practical and modeling challenges for real-time recommendation. These include:a) long-range user interactions (implicit and explicit) spanning both digital and physical channels generating temporally heterogeneous context, b) the presence of multiple interrelated products require coordinated models to support varied ad placements and personalized feeds, while balancing competing business goals. We propose FinTRec, a transformer-based framework that addresses these challenges and its operational objectives in FS. While tree-based models have traditionally been preferred in FS due to their explainability and alignment with regulatory requirements, our study demonstrate that FinTRec offers a viable and effective shift toward transformer-based architectures. Through historic simulation and live A/B test correlations, we show FinTRec consistently outperforms the production-grade tree-based baseline. The unified architecture, when fine-tuned for product adaptation, enables cross-product signal sharing, reduces training cost and technical debt, while improving offline performance across all products. To our knowledge, this is the first comprehensive study of unified sequential recommendation modeling in FS that addresses both technical and business considerations.

Physics Informed RNN-DCT Networks for Time-Dependent Partial Differential Equations

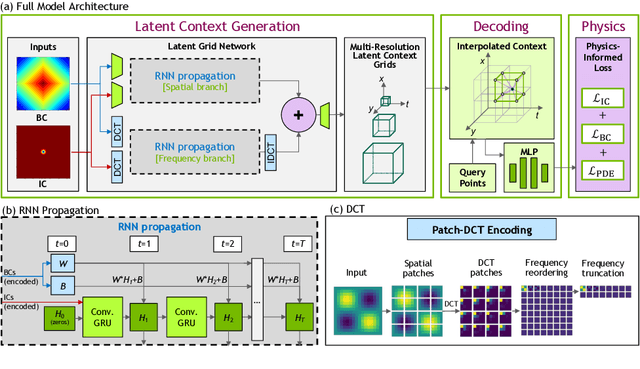
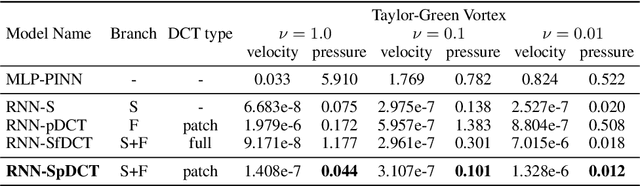
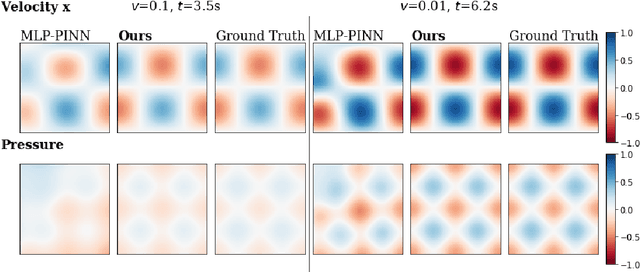
Physics-informed neural networks allow models to be trained by physical laws described by general nonlinear partial differential equations. However, traditional architectures struggle to solve more challenging time-dependent problems due to their architectural nature. In this work, we present a novel physics-informed framework for solving time-dependent partial differential equations. Using only the governing differential equations and problem initial and boundary conditions, we generate a latent representation of the problem's spatio-temporal dynamics. Our model utilizes discrete cosine transforms to encode spatial frequencies and recurrent neural networks to process the time evolution. This efficiently and flexibly produces a compressed representation which is used for additional conditioning of physics-informed models. We show experimental results on the Taylor-Green vortex solution to the Navier-Stokes equations. Our proposed model achieves state-of-the-art performance on the Taylor-Green vortex relative to other physics-informed baseline models.