Semi-Supervised Risk Control via Prediction-Powered Inference

The risk-controlling prediction sets (RCPS) framework is a general tool for transforming the output of any machine learning model to design a predictive rule with rigorous error rate control. The key idea behind this framework is to use labeled hold-out calibration data to tune a hyper-parameter that affects the error rate of the resulting prediction rule. However, the limitation of such a calibration scheme is that with limited hold-out data, the tuned hyper-parameter becomes noisy and leads to a prediction rule with an error rate that is often unnecessarily conservative. To overcome this sample-size barrier, we introduce a semi-supervised calibration procedure that leverages unlabeled data to rigorously tune the hyper-parameter without compromising statistical validity. Our procedure builds upon the prediction-powered inference framework, carefully tailoring it to risk-controlling tasks. We demonstrate the benefits and validity of our proposal through two real-data experiments: few-shot image classification and early time series classification.

Conformal Prediction is Robust to Label Noise

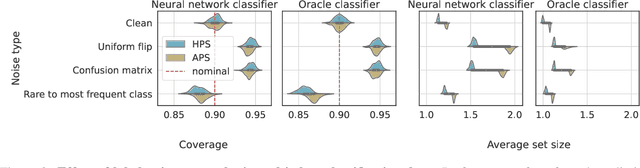
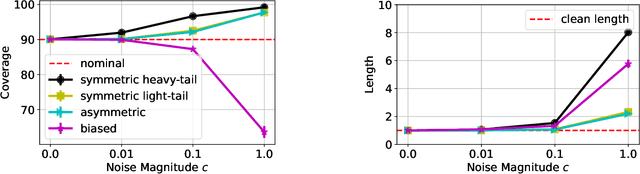
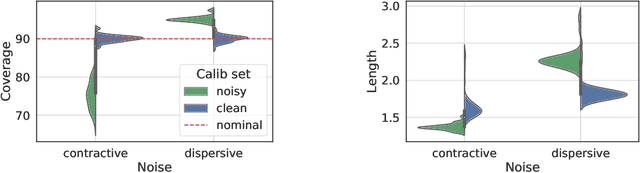
We study the robustness of conformal prediction, a powerful tool for uncertainty quantification, to label noise. Our analysis tackles both regression and classification problems, characterizing when and how it is possible to construct uncertainty sets that correctly cover the unobserved noiseless ground truth labels. Through stylized theoretical examples and practical experiments, we argue that naive conformal prediction covers the noiseless ground truth label unless the noise distribution is adversarially designed. This leads us to believe that correcting for label noise is unnecessary except for pathological data distributions or noise sources. In such cases, we can also correct for noise of bounded size in the conformal prediction algorithm in order to ensure correct coverage of the ground truth labels without score or data regularity.

Training Uncertainty-Aware Classifiers with Conformalized Deep Learning

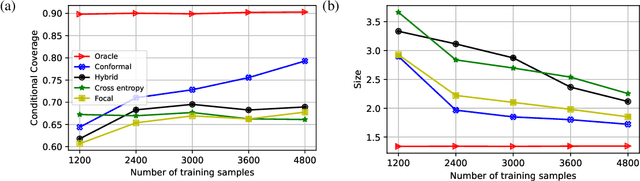
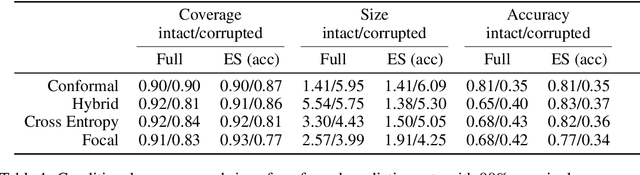
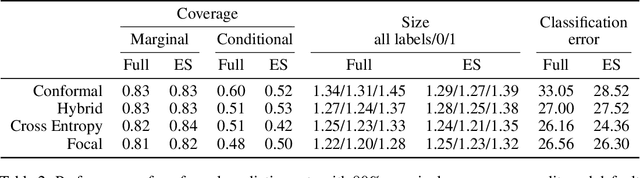
Deep neural networks are powerful tools to detect hidden patterns in data and leverage them to make predictions, but they are not designed to understand uncertainty and estimate reliable probabilities. In particular, they tend to be overconfident. We address this problem by developing a novel training algorithm that can lead to more dependable uncertainty estimates, without sacrificing predictive power. The idea is to mitigate overconfidence by minimizing a loss function, inspired by advances in conformal inference, that quantifies model uncertainty by carefully leveraging hold-out data. Experiments with synthetic and real data demonstrate this method leads to smaller conformal prediction sets with higher conditional coverage, after exact calibration with hold-out data, compared to state-of-the-art alternatives.