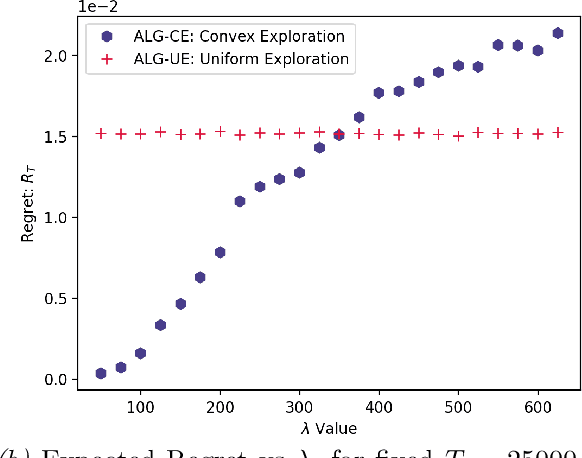
Causal Contextual Bandits with Adaptive Context

We study a variant of causal contextual bandits where the context is chosen based on an initial intervention chosen by the learner. At the beginning of each round, the learner selects an initial action, depending on which a stochastic context is revealed by the environment. Following this, the learner then selects a final action and receives a reward. Given $T$ rounds of interactions with the environment, the objective of the learner is to learn a policy (of selecting the initial and the final action) with maximum expected reward. In this paper we study the specific situation where every action corresponds to intervening on a node in some known causal graph. We extend prior work from the deterministic context setting to obtain simple regret minimization guarantees. This is achieved through an instance-dependent causal parameter, $\lambda$, which characterizes our upper bound. Furthermore, we prove that our simple regret is essentially tight for a large class of instances. A key feature of our work is that we use convex optimization to address the bandit exploration problem. We also conduct experiments to validate our theoretical results, and release our code at our project GitHub repository: https://github.com/adaptiveContextualCausalBandits/aCCB.

Delivery Optimized Discovery in Behavioral User Segmentation under Budget Constrain

Users' behavioral footprints online enable firms to discover behavior-based user segments (or, segments) and deliver segment specific messages to users. Following the discovery of segments, delivery of messages to users through preferred media channels like Facebook and Google can be challenging, as only a portion of users in a behavior segment find match in a medium, and only a fraction of those matched actually see the message (exposure). Even high quality discovery becomes futile when delivery fails. Many sophisticated algorithms exist for discovering behavioral segments; however, these ignore the delivery component. The problem is compounded because (i) the discovery is performed on the behavior data space in firms' data (e.g., user clicks), while the delivery is predicated on the static data space (e.g., geo, age) as defined by media; and (ii) firms work under budget constraint. We introduce a stochastic optimization based algorithm for delivery optimized discovery of behavioral user segmentation and offer new metrics to address the joint optimization. We leverage optimization under a budget constraint for delivery combined with a learning-based component for discovery. Extensive experiments on a public dataset from Google and a proprietary dataset show the effectiveness of our approach by simultaneously improving delivery metrics, reducing budget spend and achieving strong predictive performance in discovery.

Offsetting Unequal Competition through RL-assisted Incentive Schemes

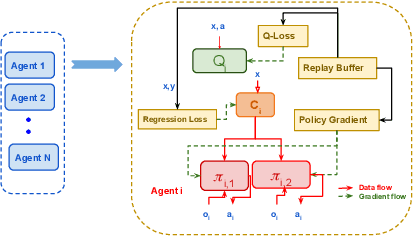
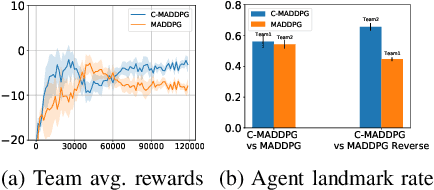
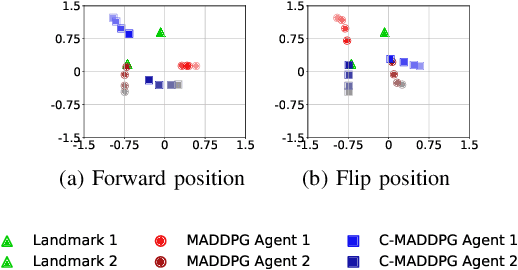
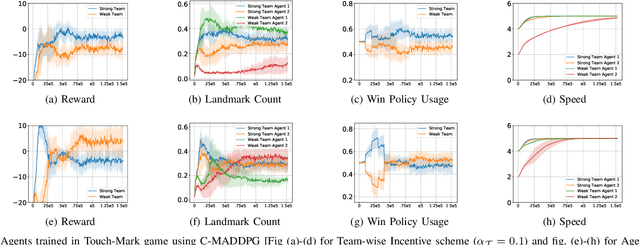
This paper investigates the dynamics of competition among organizations with unequal expertise. Multi-agent reinforcement learning has been used to simulate and understand the impact of various incentive schemes designed to offset such inequality. We design Touch-Mark, a game based on well-known multi-agent-particle-environment, where two teams (weak, strong) with unequal but changing skill levels compete against each other. For training such a game, we propose a novel controller assisted multi-agent reinforcement learning algorithm \our\, which empowers each agent with an ensemble of policies along with a supervised controller that by selectively partitioning the sample space, triggers intelligent role division among the teammates. Using C-MADDPG as an underlying framework, we propose an incentive scheme for the weak team such that the final rewards of both teams become the same. We find that in spite of the incentive, the final reward of the weak team falls short of the strong team. On inspecting, we realize that an overall incentive scheme for the weak team does not incentivize the weaker agents within that team to learn and improve. To offset this, we now specially incentivize the weaker player to learn and as a result, observe that the weak team beyond an initial phase performs at par with the stronger team. The final goal of the paper has been to formulate a dynamic incentive scheme that continuously balances the reward of the two teams. This is achieved by devising an incentive scheme enriched with an RL agent which takes minimum information from the environment.

Intervention Efficient Algorithm for Two-Stage Causal MDPs

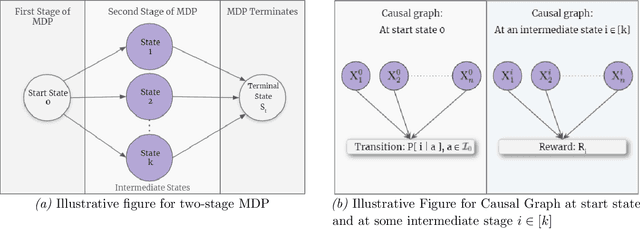
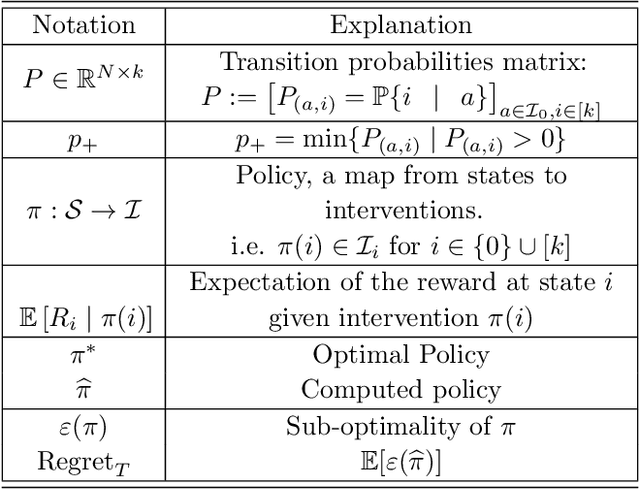
We study Markov Decision Processes (MDP) wherein states correspond to causal graphs that stochastically generate rewards. In this setup, the learner's goal is to identify atomic interventions that lead to high rewards by intervening on variables at each state. Generalizing the recent causal-bandit framework, the current work develops (simple) regret minimization guarantees for two-stage causal MDPs, with parallel causal graph at each state. We propose an algorithm that achieves an instance dependent regret bound. A key feature of our algorithm is that it utilizes convex optimization to address the exploration problem. We identify classes of instances wherein our regret guarantee is essentially tight, and experimentally validate our theoretical results.

Causal Bandits on General Graphs

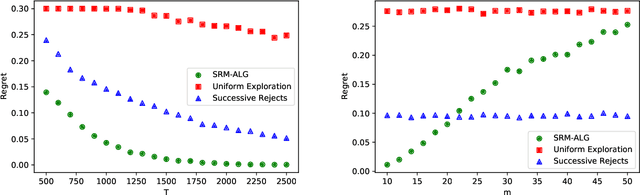
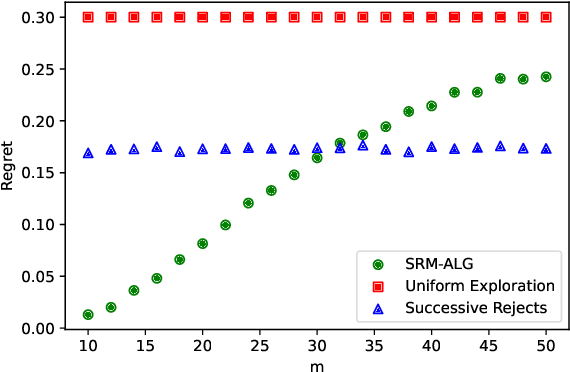
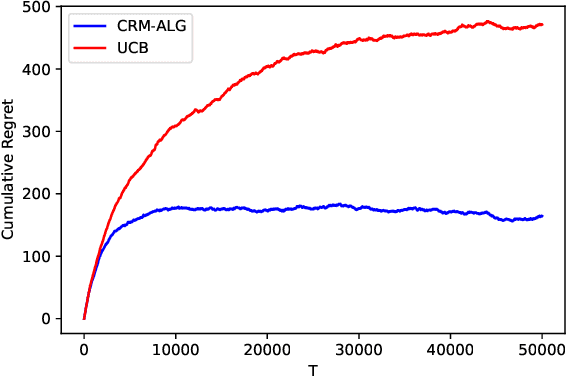
We study the problem of determining the best intervention in a Causal Bayesian Network (CBN) specified only by its causal graph. We model this as a stochastic multi-armed bandit (MAB) problem with side-information, where the interventions correspond to the arms of the bandit instance. First, we propose a simple regret minimization algorithm that takes as input a semi-Markovian causal graph with atomic interventions and possibly unobservable variables, and achieves $\tilde{O}(\sqrt{M/T})$ expected simple regret, where $M$ is dependent on the input CBN and could be very small compared to the number of arms. We also show that this is almost optimal for CBNs described by causal graphs having an $n$-ary tree structure. Our simple regret minimization results, both upper and lower bound, subsume previous results in the literature, which assumed additional structural restrictions on the input causal graph. In particular, our results indicate that the simple regret guarantee of our proposed algorithm can only be improved by considering more nuanced structural restrictions on the causal graph. Next, we propose a cumulative regret minimization algorithm that takes as input a general causal graph with all observable nodes and atomic interventions and performs better than the optimal MAB algorithm that does not take causal side-information into account. We also experimentally compare both our algorithms with the best known algorithms in the literature. To the best of our knowledge, this work gives the first simple and cumulative regret minimization algorithms for CBNs with general causal graphs under atomic interventions and having unobserved confounders.

Dis-entangling Mixture of Interventions on a Causal Bayesian Network Using Aggregate Observations

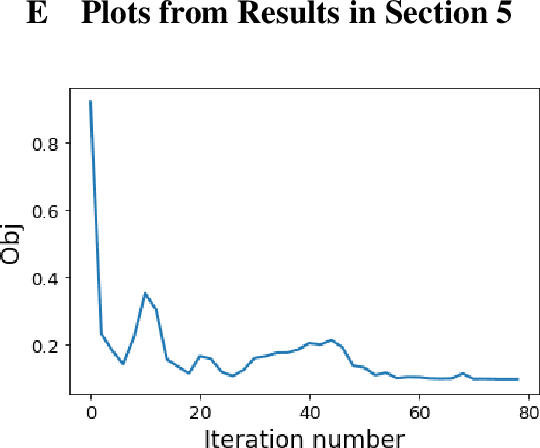
We study the problem of separating a mixture of distributions, all of which come from interventions on a known causal bayesian network. Given oracle access to marginals of all distributions resulting from interventions on the network, and estimates of marginals from the mixture distribution, we want to recover the mixing proportions of different mixture components. We show that in the worst case, mixing proportions cannot be identified using marginals only. If exact marginals of the mixture distribution were known, under a simple assumption of excluding a few distributions from the mixture, we show that the mixing proportions become identifiable. Our identifiability proof is constructive and gives an efficient algorithm recovering the mixing proportions exactly. When exact marginals are not available, we design an optimization framework to estimate the mixing proportions. Our problem is motivated from a real-world scenario of an e-commerce business, where multiple interventions occur at a given time, leading to deviations in expected metrics. We conduct experiments on the well known publicly available ALARM network and on a proprietary dataset from a large e-commerce company validating the performance of our method.