Shallow diffusion networks provably learn hidden low-dimensional structure

Diffusion-based generative models provide a powerful framework for learning to sample from a complex target distribution. The remarkable empirical success of these models applied to high-dimensional signals, including images and video, stands in stark contrast to classical results highlighting the curse of dimensionality for distribution recovery. In this work, we take a step towards understanding this gap through a careful analysis of learning diffusion models over the Barron space of single layer neural networks. In particular, we show that these shallow models provably adapt to simple forms of low dimensional structure, thereby avoiding the curse of dimensionality. We combine our results with recent analyses of sampling with diffusion models to provide an end-to-end sample complexity bound for learning to sample from structured distributions. Importantly, our results do not require specialized architectures tailored to particular latent structures, and instead rely on the low-index structure of the Barron space to adapt to the underlying distribution.

Wide Neural Networks Trained with Weight Decay Provably Exhibit Neural Collapse

Deep neural networks (DNNs) at convergence consistently represent the training data in the last layer via a highly symmetric geometric structure referred to as neural collapse. This empirical evidence has spurred a line of theoretical research aimed at proving the emergence of neural collapse, mostly focusing on the unconstrained features model. Here, the features of the penultimate layer are free variables, which makes the model data-agnostic and, hence, puts into question its ability to capture DNN training. Our work addresses the issue, moving away from unconstrained features and studying DNNs that end with at least two linear layers. We first prove generic guarantees on neural collapse that assume (i) low training error and balancedness of the linear layers (for within-class variability collapse), and (ii) bounded conditioning of the features before the linear part (for orthogonality of class-means, as well as their alignment with weight matrices). We then show that such assumptions hold for gradient descent training with weight decay: (i) for networks with a wide first layer, we prove low training error and balancedness, and (ii) for solutions that are either nearly optimal or stable under large learning rates, we additionally prove the bounded conditioning. Taken together, our results are the first to show neural collapse in the end-to-end training of DNNs.

How DNNs break the Curse of Dimensionality: Compositionality and Symmetry Learning

We show that deep neural networks (DNNs) can efficiently learn any composition of functions with bounded $F_{1}$-norm, which allows DNNs to break the curse of dimensionality in ways that shallow networks cannot. More specifically, we derive a generalization bound that combines a covering number argument for compositionality, and the $F_{1}$-norm (or the related Barron norm) for large width adaptivity. We show that the global minimizer of the regularized loss of DNNs can fit for example the composition of two functions $f^{*}=h\circ g$ from a small number of observations, assuming $g$ is smooth/regular and reduces the dimensionality (e.g. $g$ could be the modulo map of the symmetries of $f^{*}$), so that $h$ can be learned in spite of its low regularity. The measures of regularity we consider is the Sobolev norm with different levels of differentiability, which is well adapted to the $F_{1}$ norm. We compute scaling laws empirically and observe phase transitions depending on whether $g$ or $h$ is harder to learn, as predicted by our theory.

Hamiltonian Mechanics of Feature Learning: Bottleneck Structure in Leaky ResNets

We study Leaky ResNets, which interpolate between ResNets ($\tilde{L}=0$) and Fully-Connected nets ($\tilde{L}\to\infty$) depending on an 'effective depth' hyper-parameter $\tilde{L}$. In the infinite depth limit, we study 'representation geodesics' $A_{p}$: continuous paths in representation space (similar to NeuralODEs) from input $p=0$ to output $p=1$ that minimize the parameter norm of the network. We give a Lagrangian and Hamiltonian reformulation, which highlight the importance of two terms: a kinetic energy which favors small layer derivatives $\partial_{p}A_{p}$ and a potential energy that favors low-dimensional representations, as measured by the 'Cost of Identity'. The balance between these two forces offers an intuitive understanding of feature learning in ResNets. We leverage this intuition to explain the emergence of a bottleneck structure, as observed in previous work: for large $\tilde{L}$ the potential energy dominates and leads to a separation of timescales, where the representation jumps rapidly from the high dimensional inputs to a low-dimensional representation, move slowly inside the space of low-dimensional representations, before jumping back to the potentially high-dimensional outputs. Inspired by this phenomenon, we train with an adaptive layer step-size to adapt to the separation of timescales.

Mixed Dynamics In Linear Networks: Unifying the Lazy and Active Regimes

The training dynamics of linear networks are well studied in two distinct setups: the lazy regime and balanced/active regime, depending on the initialization and width of the network. We provide a surprisingly simple unyfing formula for the evolution of the learned matrix that contains as special cases both lazy and balanced regimes but also a mixed regime in between the two. In the mixed regime, a part of the network is lazy while the other is balanced. More precisely the network is lazy along singular values that are below a certain threshold and balanced along those that are above the same threshold. At initialization, all singular values are lazy, allowing for the network to align itself with the task, so that later in time, when some of the singular value cross the threshold and become active they will converge rapidly (convergence in the balanced regime is notoriously difficult in the absence of alignment). The mixed regime is the `best of both worlds': it converges from any random initialization (in contrast to balanced dynamics which require special initialization), and has a low rank bias (absent in the lazy dynamics). This allows us to prove an almost complete phase diagram of training behavior as a function of the variance at initialization and the width, for a MSE training task.

Which Frequencies do CNNs Need? Emergent Bottleneck Structure in Feature Learning

We describe the emergence of a Convolution Bottleneck (CBN) structure in CNNs, where the network uses its first few layers to transform the input representation into a representation that is supported only along a few frequencies and channels, before using the last few layers to map back to the outputs. We define the CBN rank, which describes the number and type of frequencies that are kept inside the bottleneck, and partially prove that the parameter norm required to represent a function $f$ scales as depth times the CBN rank $f$. We also show that the parameter norm depends at next order on the regularity of $f$. We show that any network with almost optimal parameter norm will exhibit a CBN structure in both the weights and - under the assumption that the network is stable under large learning rate - the activations, which motivates the common practice of down-sampling; and we verify that the CBN results still hold with down-sampling. Finally we use the CBN structure to interpret the functions learned by CNNs on a number of tasks.

Bottleneck Structure in Learned Features: Low-Dimension vs Regularity Tradeoff

Previous work has shown that DNNs with large depth $L$ and $L_{2}$-regularization are biased towards learning low-dimensional representations of the inputs, which can be interpreted as minimizing a notion of rank $R^{(0)}(f)$ of the learned function $f$, conjectured to be the Bottleneck rank. We compute finite depth corrections to this result, revealing a measure $R^{(1)}$ of regularity which bounds the pseudo-determinant of the Jacobian $\left|Jf(x)\right|_{+}$ and is subadditive under composition and addition. This formalizes a balance between learning low-dimensional representations and minimizing complexity/irregularity in the feature maps, allowing the network to learn the `right' inner dimension. We also show how large learning rates also control the regularity of the learned function. Finally, we use these theoretical tools to prove the conjectured bottleneck structure in the learned features as $L\to\infty$: for large depths, almost all hidden representations concentrates around $R^{(0)}(f)$-dimensional representations. These limiting low-dimensional representation can be described using the second correction $R^{(2)}$.

Implicit bias of SGD in $L_{2}$-regularized linear DNNs: One-way jumps from high to low rank

The $L_{2}$-regularized loss of Deep Linear Networks (DLNs) with more than one hidden layers has multiple local minima, corresponding to matrices with different ranks. In tasks such as matrix completion, the goal is to converge to the local minimum with the smallest rank that still fits the training data. While rank-underestimating minima can easily be avoided since they do not fit the data, gradient descent might get stuck at rank-overestimating minima. We show that with SGD, there is always a probability to jump from a higher rank minimum to a lower rank one, but the probability of jumping back is zero. More precisely, we define a sequence of sets $B_{1}\subset B_{2}\subset\cdots\subset B_{R}$ so that $B_{r}$ contains all minima of rank $r$ or less (and not more) that are absorbing for small enough ridge parameters $\lambda$ and learning rates $\eta$: SGD has prob. 0 of leaving $B_{r}$, and from any starting point there is a non-zero prob. for SGD to go in $B_{r}$.

Implicit Bias of Large Depth Networks: a Notion of Rank for Nonlinear Functions

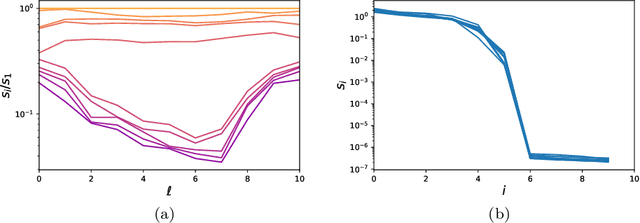
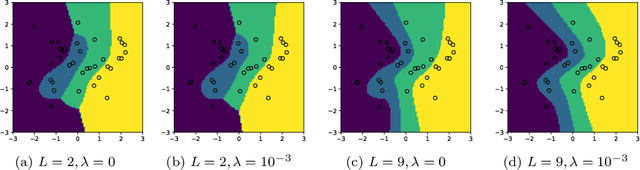
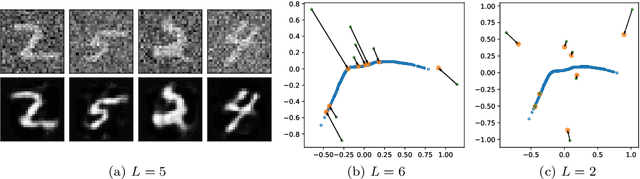
We show that the representation cost of fully connected neural networks with homogeneous nonlinearities - which describes the implicit bias in function space of networks with $L_2$-regularization or with losses such as the cross-entropy - converges as the depth of the network goes to infinity to a notion of rank over nonlinear functions. We then inquire under which conditions the global minima of the loss recover the `true' rank of the data: we show that for too large depths the global minimum will be approximately rank 1 (underestimating the rank); we then argue that there is a range of depths which grows with the number of datapoints where the true rank is recovered. Finally, we discuss the effect of the rank of a classifier on the topology of the resulting class boundaries and show that autoencoders with optimal nonlinear rank are naturally denoising.

Feature Learning in $L_{2}$-regularized DNNs: Attraction/Repulsion and Sparsity

We study the loss surface of DNNs with $L_{2}$ regularization. We show that the loss in terms of the parameters can be reformulated into a loss in terms of the layerwise activations $Z_{\ell}$ of the training set. This reformulation reveals the dynamics behind feature learning: each hidden representations $Z_{\ell}$ are optimal w.r.t. to an attraction/repulsion problem and interpolate between the input and output representations, keeping as little information from the input as necessary to construct the activation of the next layer. For positively homogeneous non-linearities, the loss can be further reformulated in terms of the covariances of the hidden representations, which takes the form of a partially convex optimization over a convex cone. This second reformulation allows us to prove a sparsity result for homogeneous DNNs: any local minimum of the $L_{2}$-regularized loss can be achieved with at most $N(N+1)$ neurons in each hidden layer (where $N$ is the size of the training set). We show that this bound is tight by giving an example of a local minimum which requires $N^{2}/4$ hidden neurons. But we also observe numerically that in more traditional settings much less than $N^{2}$ neurons are required to reach the minima.