Aritra Ghosh
Context-Aware Attentive Knowledge Tracing
Jul 24, 2020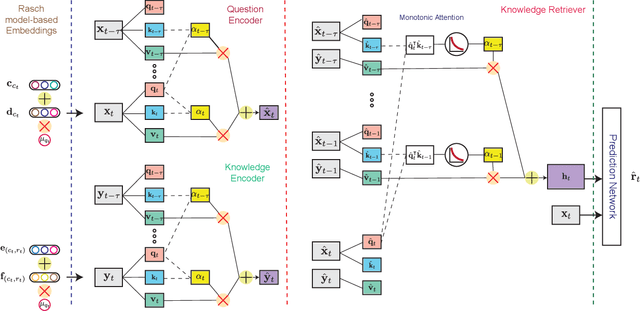
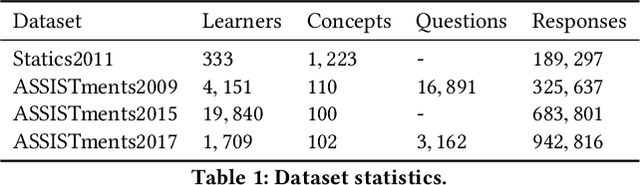

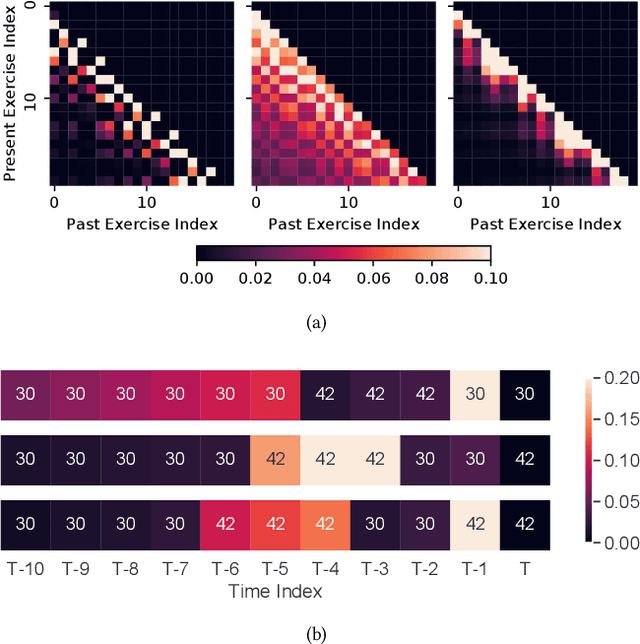
Abstract:Knowledge tracing (KT) refers to the problem of predicting future learner performance given their past performance in educational applications. Recent developments in KT using flexible deep neural network-based models excel at this task. However, these models often offer limited interpretability, thus making them insufficient for personalized learning, which requires using interpretable feedback and actionable recommendations to help learners achieve better learning outcomes. In this paper, we propose attentive knowledge tracing (AKT), which couples flexible attention-based neural network models with a series of novel, interpretable model components inspired by cognitive and psychometric models. AKT uses a novel monotonic attention mechanism that relates a learner's future responses to assessment questions to their past responses; attention weights are computed using exponential decay and a context-aware relative distance measure, in addition to the similarity between questions. Moreover, we use the Rasch model to regularize the concept and question embeddings; these embeddings are able to capture individual differences among questions on the same concept without using an excessive number of parameters. We conduct experiments on several real-world benchmark datasets and show that AKT outperforms existing KT methods (by up to $6\%$ in AUC in some cases) on predicting future learner responses. We also conduct several case studies and show that AKT exhibits excellent interpretability and thus has potential for automated feedback and personalization in real-world educational settings.
Optimal Bidding Strategy without Exploration in Real-time Bidding
Mar 31, 2020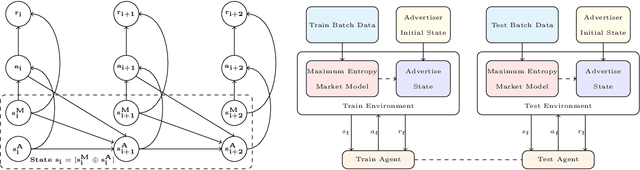
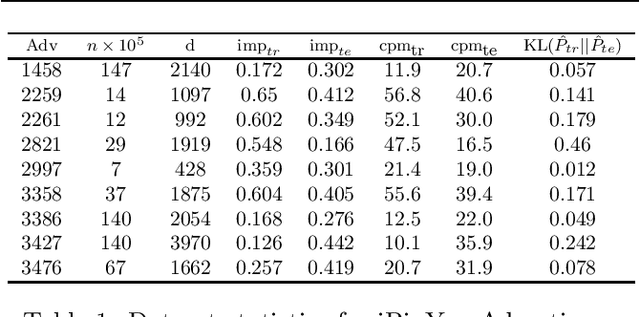
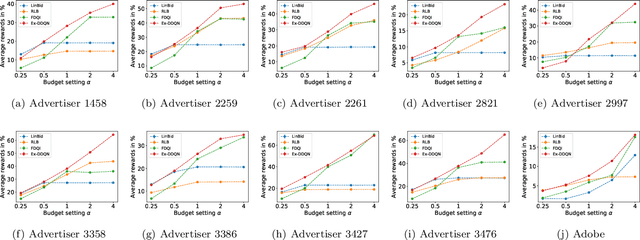
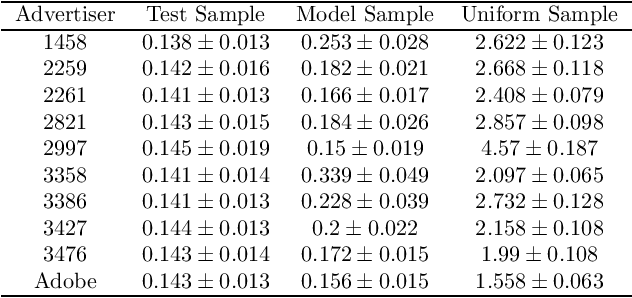
Abstract:Maximizing utility with a budget constraint is the primary goal for advertisers in real-time bidding (RTB) systems. The policy maximizing the utility is referred to as the optimal bidding strategy. Earlier works on optimal bidding strategy apply model-based batch reinforcement learning methods which can not generalize to unknown budget and time constraint. Further, the advertiser observes a censored market price which makes direct evaluation infeasible on batch test datasets. Previous works ignore the losing auctions to alleviate the difficulty with censored states; thus significantly modifying the test distribution. We address the challenge of lacking a clear evaluation procedure as well as the error propagated through batch reinforcement learning methods in RTB systems. We exploit two conditional independence structures in the sequential bidding process that allow us to propose a novel practical framework using the maximum entropy principle to imitate the behavior of the true distribution observed in real-time traffic. Moreover, the framework allows us to train a model that can generalize to the unseen budget conditions than limit only to those observed in history. We compare our methods on two real-world RTB datasets with several baselines and demonstrate significantly improved performance under various budget settings.
Scalable Bid Landscape Forecasting in Real-time Bidding
Jan 18, 2020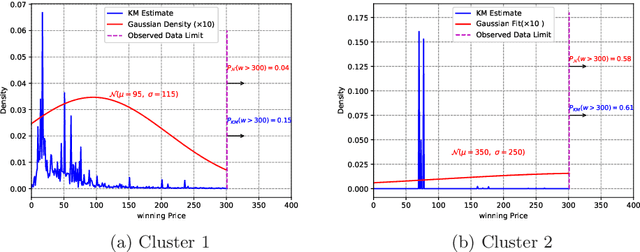
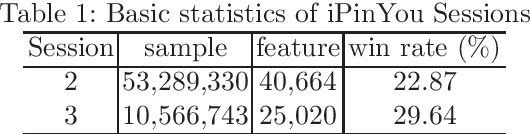
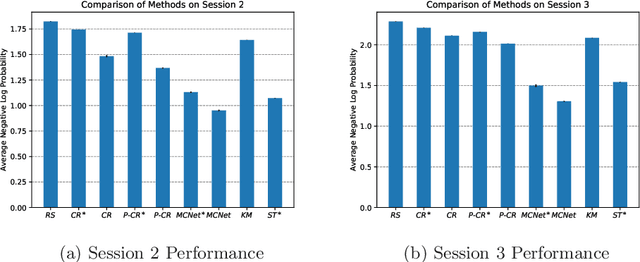
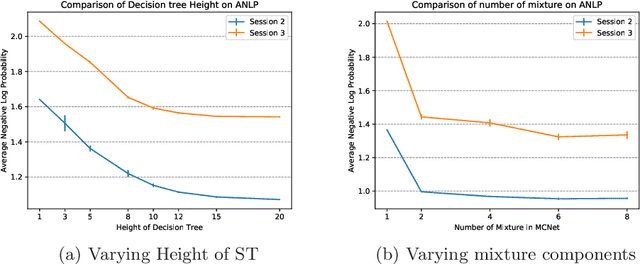
Abstract:In programmatic advertising, ad slots are usually sold using second-price (SP) auctions in real-time. The highest bidding advertiser wins but pays only the second-highest bid (known as the winning price). In SP, for a single item, the dominant strategy of each bidder is to bid the true value from the bidder's perspective. However, in a practical setting, with budget constraints, bidding the true value is a sub-optimal strategy. Hence, to devise an optimal bidding strategy, it is of utmost importance to learn the winning price distribution accurately. Moreover, a demand-side platform (DSP), which bids on behalf of advertisers, observes the winning price if it wins the auction. For losing auctions, DSPs can only treat its bidding price as the lower bound for the unknown winning price. In literature, typically censored regression is used to model such partially observed data. A common assumption in censored regression is that the winning price is drawn from a fixed variance (homoscedastic) uni-modal distribution (most often Gaussian). However, in reality, these assumptions are often violated. We relax these assumptions and propose a heteroscedastic fully parametric censored regression approach, as well as a mixture density censored network. Our approach not only generalizes censored regression but also provides flexibility to model arbitrarily distributed real-world data. Experimental evaluation on the publicly available dataset for winning price estimation demonstrates the effectiveness of our method. Furthermore, we evaluate our algorithm on one of the largest demand-side platforms and significant improvement has been achieved in comparison with the baseline solutions.
Robust Loss Functions under Label Noise for Deep Neural Networks
Dec 27, 2017
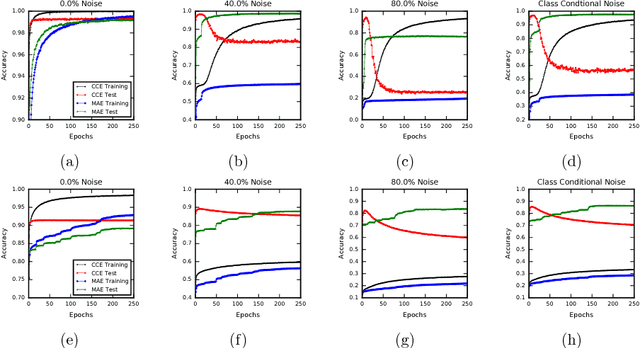
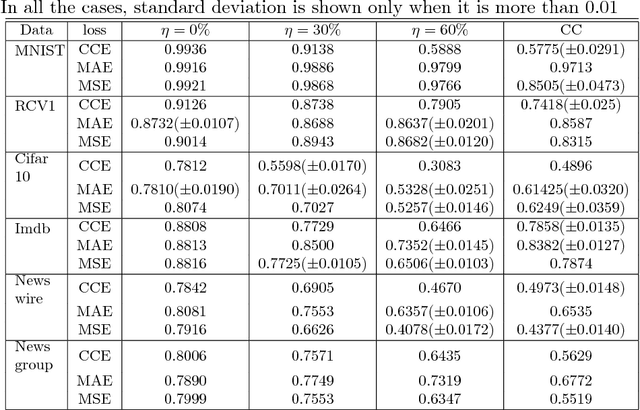
Abstract:In many applications of classifier learning, training data suffers from label noise. Deep networks are learned using huge training data where the problem of noisy labels is particularly relevant. The current techniques proposed for learning deep networks under label noise focus on modifying the network architecture and on algorithms for estimating true labels from noisy labels. An alternate approach would be to look for loss functions that are inherently noise-tolerant. For binary classification there exist theoretical results on loss functions that are robust to label noise. In this paper, we provide some sufficient conditions on a loss function so that risk minimization under that loss function would be inherently tolerant to label noise for multiclass classification problems. These results generalize the existing results on noise-tolerant loss functions for binary classification. We study some of the widely used loss functions in deep networks and show that the loss function based on mean absolute value of error is inherently robust to label noise. Thus standard back propagation is enough to learn the true classifier even under label noise. Through experiments, we illustrate the robustness of risk minimization with such loss functions for learning neural networks.
On the Robustness of Decision Tree Learning under Label Noise
Aug 26, 2016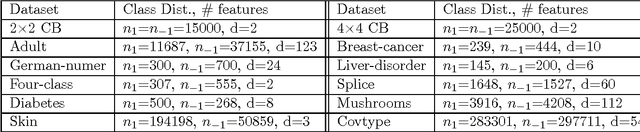
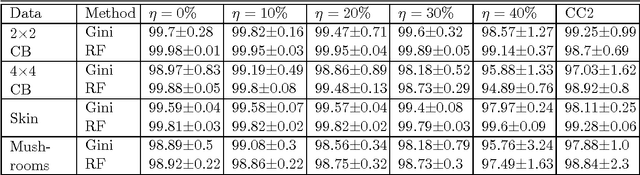
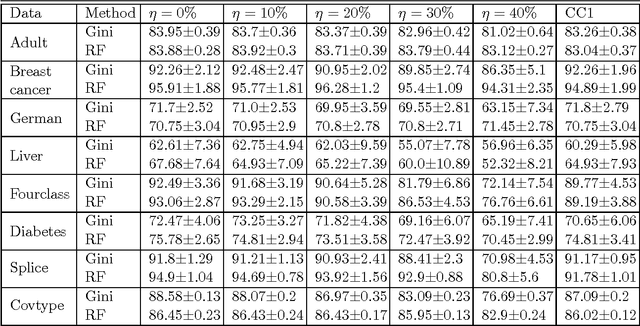
Abstract:In most practical problems of classifier learning, the training data suffers from the label noise. Hence, it is important to understand how robust is a learning algorithm to such label noise. This paper presents some theoretical analysis to show that many popular decision tree algorithms are robust to symmetric label noise under large sample size. We also present some sample complexity results which provide some bounds on the sample size for the robustness to hold with a high probability. Through extensive simulations we illustrate this robustness.
Making Risk Minimization Tolerant to Label Noise
Sep 10, 2015
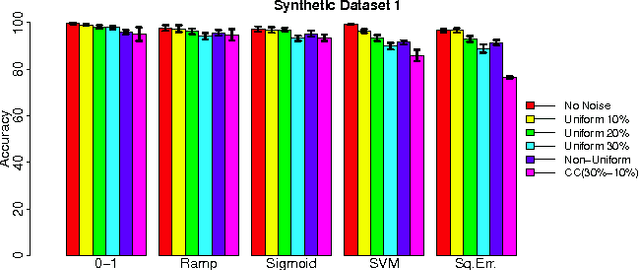
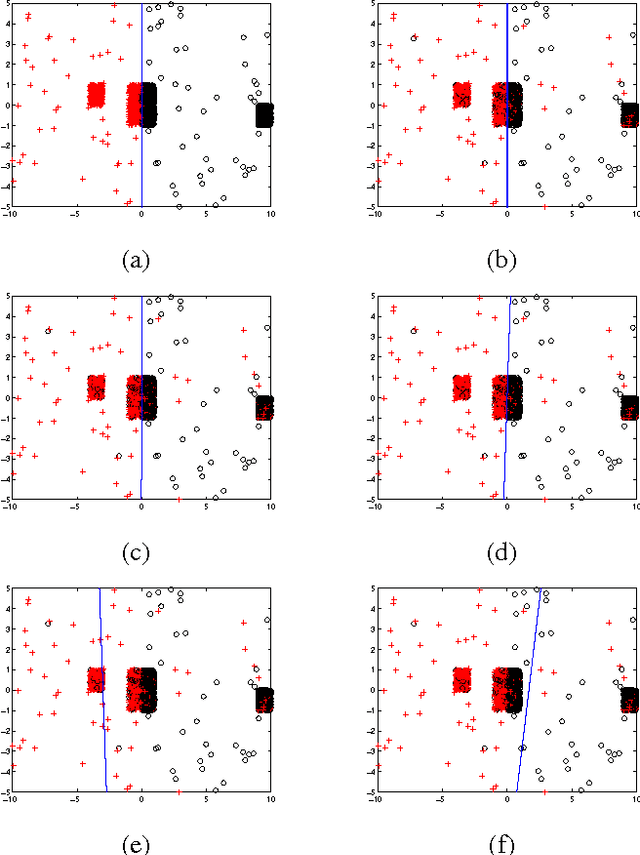

Abstract:In many applications, the training data, from which one needs to learn a classifier, is corrupted with label noise. Many standard algorithms such as SVM perform poorly in presence of label noise. In this paper we investigate the robustness of risk minimization to label noise. We prove a sufficient condition on a loss function for the risk minimization under that loss to be tolerant to uniform label noise. We show that the $0-1$ loss, sigmoid loss, ramp loss and probit loss satisfy this condition though none of the standard convex loss functions satisfy it. We also prove that, by choosing a sufficiently large value of a parameter in the loss function, the sigmoid loss, ramp loss and probit loss can be made tolerant to non-uniform label noise also if we can assume the classes to be separable under noise-free data distribution. Through extensive empirical studies, we show that risk minimization under the $0-1$ loss, the sigmoid loss and the ramp loss has much better robustness to label noise when compared to the SVM algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge