Multi-RIS-Empowered Communication Systems: Capacity Analysis and Optimization

In this chapter, using statistical physics methods, asymptotic closed-form expressions for the mean and variance of the mutual information for a multi-antenna transmitter-receiver pair in the presence of multiple Reconfigurable Intelligent Surfaces (RISs) are presented. While nominally valid in the large-system limit, it is shown that the derived Gaussian approximation for the mutual information can be quite accurate, even for modest-sized antenna arrays and metasurfaces. The above results are particularly useful when fast-fading conditions are present, which renders channel estimation challenging. The derived analysis indicates that, when the channel close to an RIS is correlated, for instance due to small angle spread which is reasonable for wireless systems with increasing carrier frequencies, the communication link benefits significantly from statistical RIS optimization, resulting in gains that are surprisingly higher than the nearly uncorrelated case. More importantly, the presented novel asymptotic properties of the correlation matrices of the impinging and outgoing signals at the RISs can be deployed to optimize the metasurfaces without brute-force numerical optimization. The numerical investigation demonstrates that, when the desired reflection from any of the RISs departs significantly from geometrical optics, the metasurfaces can be optimized to provide robust communication links, without significant need for their optimal placement.

On the Uplink Performance of Finite-Capacity Radio Stripes

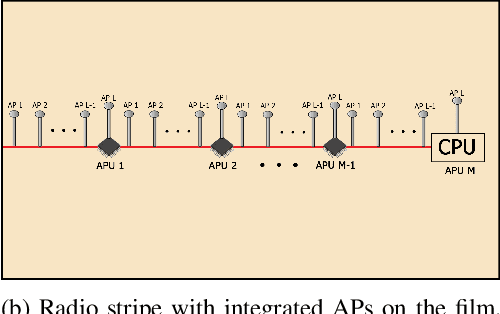
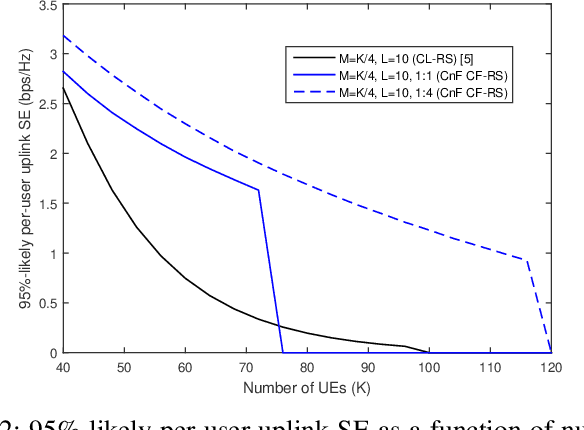
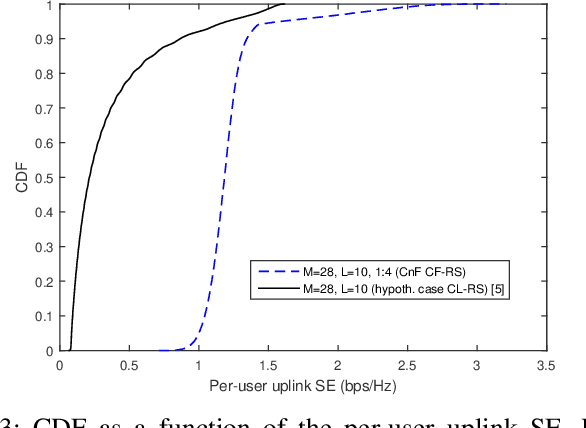
Cell-Free (CF) Massive MIMO (mMIMO) is a technology which can potentially augment not only the deployment of 5G, but also the deployment of beyond 5G (B5G) wireless networks. However, the cost for rolling out such systems may be significant. Radio stripes form a promising solution which offers the potential of scalability at a reduced price. This paper investigates the uplink scenario of a CF mMIMO system, implemented with a limited-capacity radio stripe which integrates a novel arrangement of access points (APs), fully exploiting macro-diversity benefits. We also analyze a heuristic Compare-and-Forward (CnF) strategy, which, by comparing normalized linear minimum mean square error (N-LMMSE) soft estimates, enables optimal dynamic cooperation clustering, thus leading to a user-centric radio stripe network approach. Aiming at maximizing the per-user uplink spectral efficiency (SE), we ensure that, under finite capacity constraints, our solution can guarantee better performance than existing radio stripe architectures, especially when system size increases.

Boltzmann meets Nash: Energy-efficient routing in optical networks under uncertainty

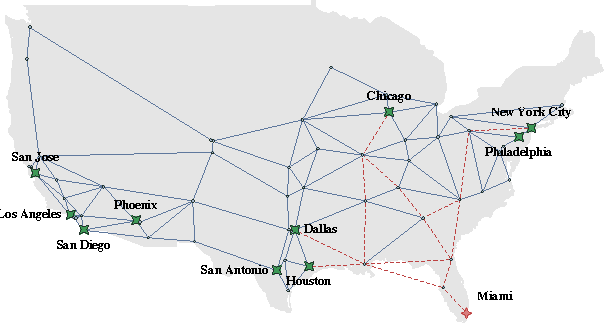
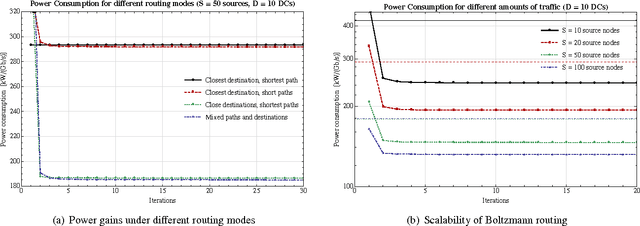
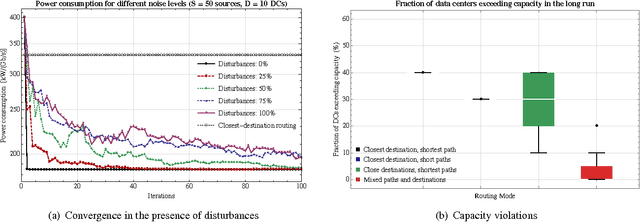
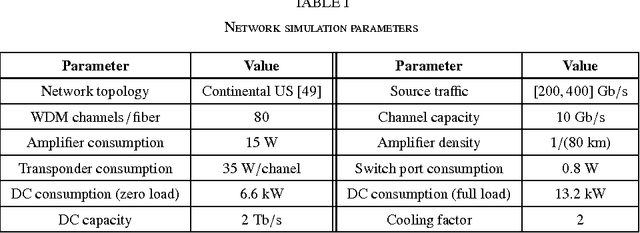
Motivated by the massive deployment of power-hungry data centers for service provisioning, we examine the problem of routing in optical networks with the aim of minimizing traffic-driven power consumption. To tackle this issue, routing must take into account energy efficiency as well as capacity considerations; moreover, in rapidly-varying network environments, this must be accomplished in a real-time, distributed manner that remains robust in the presence of random disturbances and noise. In view of this, we derive a pricing scheme whose Nash equilibria coincide with the network's socially optimum states, and we propose a distributed learning method based on the Boltzmann distribution of statistical mechanics. Using tools from stochastic calculus, we show that the resulting Boltzmann routing scheme exhibits remarkable convergence properties under uncertainty: specifically, the long-term average of the network's power consumption converges within $\varepsilon$ of its minimum value in time which is at most $\tilde O(1/\varepsilon^2)$, irrespective of the fluctuations' magnitude; additionally, if the network admits a strict, non-mixing optimum state, the algorithm converges to it - again, no matter the noise level. Our analysis is supplemented by extensive numerical simulations which show that Boltzmann routing can lead to a significant decrease in power consumption over basic, shortest-path routing schemes in realistic network conditions.

Distributed Learning Policies for Power Allocation in Multiple Access Channels

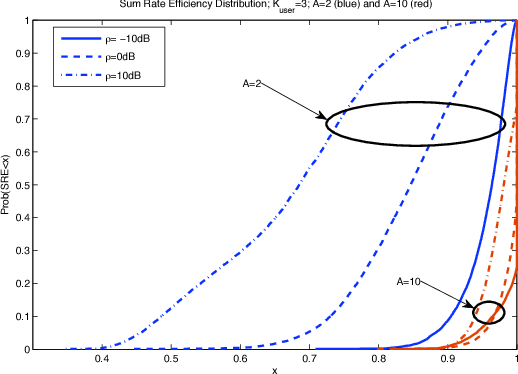
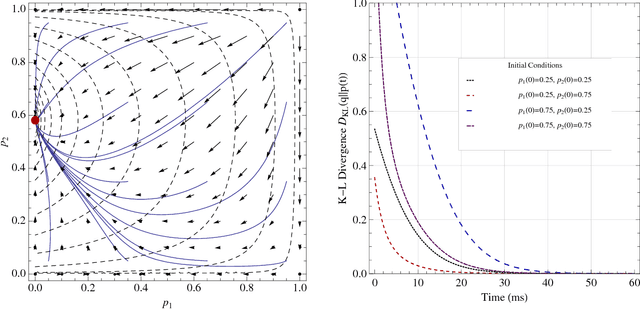
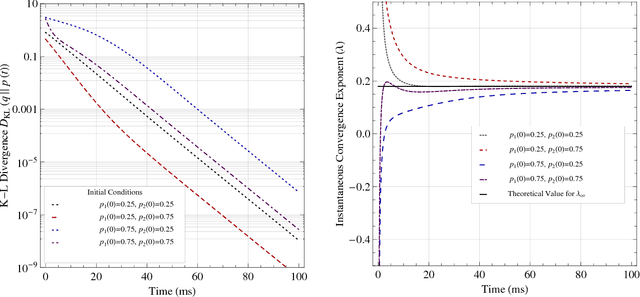
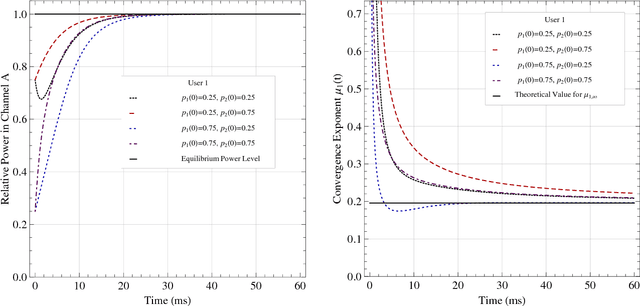
We analyze the problem of distributed power allocation for orthogonal multiple access channels by considering a continuous non-cooperative game whose strategy space represents the users' distribution of transmission power over the network's channels. When the channels are static, we find that this game admits an exact potential function and this allows us to show that it has a unique equilibrium almost surely. Furthermore, using the game's potential property, we derive a modified version of the replicator dynamics of evolutionary game theory which applies to this continuous game, and we show that if the network's users employ a distributed learning scheme based on these dynamics, then they converge to equilibrium exponentially quickly. On the other hand, a major challenge occurs if the channels do not remain static but fluctuate stochastically over time, following a stationary ergodic process. In that case, the associated ergodic game still admits a unique equilibrium, but the learning analysis becomes much more complicated because the replicator dynamics are no longer deterministic. Nonetheless, by employing results from the theory of stochastic approximation, we show that users still converge to the game's unique equilibrium. Our analysis hinges on a game-theoretical result which is of independent interest: in finite player games which admit a (possibly nonlinear) convex potential function, the replicator dynamics (suitably modified to account for nonlinear payoffs) converge to an eps-neighborhood of an equilibrium at time of order O(log(1/eps)).