Adaptive Basis Function Selection for Computationally Efficient Predictions

Basis Function (BF) expansions are a cornerstone of any engineer's toolbox for computational function approximation which shares connections with both neural networks and Gaussian processes. Even though BF expansions are an intuitive and straightforward model to use, they suffer from quadratic computational complexity in the number of BFs if the predictive variance is to be computed. We develop a method to automatically select the most important BFs for prediction in a sub-domain of the model domain. This significantly reduces the computational complexity of computing predictions while maintaining predictive accuracy. The proposed method is demonstrated using two numerical examples, where reductions up to 50-75% are possible without significantly reducing the predictive accuracy.

Exploiting Hankel-Toeplitz Structures for Fast Computation of Kernel Precision Matrices

The Hilbert-space Gaussian Process (HGP) approach offers a hyperparameter-independent basis function approximation for speeding up Gaussian Process (GP) inference by projecting the GP onto M basis functions. These properties result in a favorable data-independent $\mathcal{O}(M^3)$ computational complexity during hyperparameter optimization but require a dominating one-time precomputation of the precision matrix costing $\mathcal{O}(NM^2)$ operations. In this paper, we lower this dominating computational complexity to $\mathcal{O}(NM)$ with no additional approximations. We can do this because we realize that the precision matrix can be split into a sum of Hankel-Toeplitz matrices, each having $\mathcal{O}(M)$ unique entries. Based on this realization we propose computing only these unique entries at $\mathcal{O}(NM)$ costs. Further, we develop two theorems that prescribe sufficient conditions for the complexity reduction to hold generally for a wide range of other approximate GP models, such as the Variational Fourier Feature (VFF) approach. The two theorems do this with no assumptions on the data and no additional approximations of the GP models themselves. Thus, our contribution provides a pure speed-up of several existing, widely used, GP approximations, without further approximations.

Extended target tracking utilizing machine-learning software -- with applications to animal classification

This paper considers the problem of detecting and tracking objects in a sequence of images. The problem is formulated in a filtering framework, using the output of object-detection algorithms as measurements. An extension to the filtering formulation is proposed that incorporates class information from the previous frame to robustify the classification, even if the object-detection algorithm outputs an incorrect prediction. Further, the properties of the object-detection algorithm are exploited to quantify the uncertainty of the bounding box detection in each frame. The complete filtering method is evaluated on camera trap images of the four large Swedish carnivores, bear, lynx, wolf, and wolverine. The experiments show that the class tracking formulation leads to a more robust classification.

Unified Linearization-based Nonlinear Filtering

This letter shows that the following three classes of recursive state estimation filters: standard filters, such as the extended Kalman filter; iterated filters, such as the iterated unscented Kalman filter; and dynamically iterated filters, such as the dynamically iterated posterior linearization filters; can be unified in terms of a general algorithm. The general algorithm highlights the strong similarities between specific filtering algorithms in the three filter classes and facilitates an in-depth understanding of the pros and cons of the different filter classes and algorithms. We end with a numerical example showing the estimation accuracy differences between the three classes of filters when applied to a nonlinear localization problem.

On the Relationship Between Iterated Statistical Linearization and Quasi-Newton Methods

This letter investigates relationships between iterated filtering algorithms based on statistical linearization, such as the iterated unscented Kalman filter (IUKF), and filtering algorithms based on quasi-Newton (QN) methods, such as the QN iterated extended Kalman filter (QN-IEKF). Firstly, it is shown that the IUKF and the iterated posterior linearization filter (IPLF) can be viewed as QN algorithms, by finding a Hessian correction in the QN-IEKF such that the IPLF iterate updates are identical to that of the QN-IEKF. Secondly, it is shown that the IPLF/IUKF update can be rewritten such that it is approximately identical to the QN-IEKF, albeit for an additional correction term. This enables a richer understanding of the properties of iterated filtering algorithms based on statistical linearization.

Iterated Filters for Nonlinear Transition Models

A new class of iterated linearization-based nonlinear filters, dubbed dynamically iterated filters, is presented. Contrary to regular iterated filters such as the iterated extended Kalman filter (IEKF), iterated unscented Kalman filter (IUKF) and iterated posterior linearization filter (IPLF), dynamically iterated filters also take nonlinearities in the transition model into account. The general filtering algorithm is shown to essentially be a (locally over one time step) iterated Rauch-Tung-Striebel smoother. Three distinct versions of the dynamically iterated filters are especially investigated: analogues to the IEKF, IUKF and IPLF. The developed algorithms are evaluated on 25 different noise configurations of a tracking problem with a nonlinear transition model and linear measurement model, a scenario where conventional iterated filters are not useful. Even in this "simple" scenario, the dynamically iterated filters are shown to have superior root mean-squared error performance as compared to their respective baselines, the EKF and UKF. Particularly, even though the EKF diverges in 22 out of 25 configurations, the dynamically iterated EKF remains stable in 20 out of 25 scenarios, only diverging under high noise.

Online Joint State Inference and Learning of Partially Unknown State-Space Models

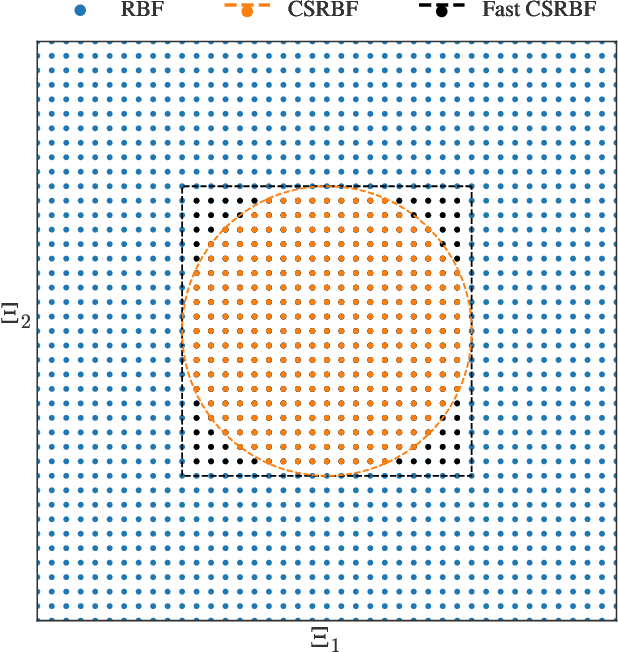
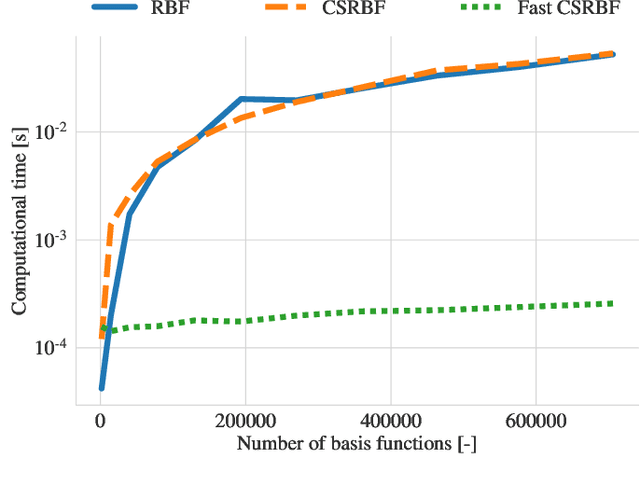
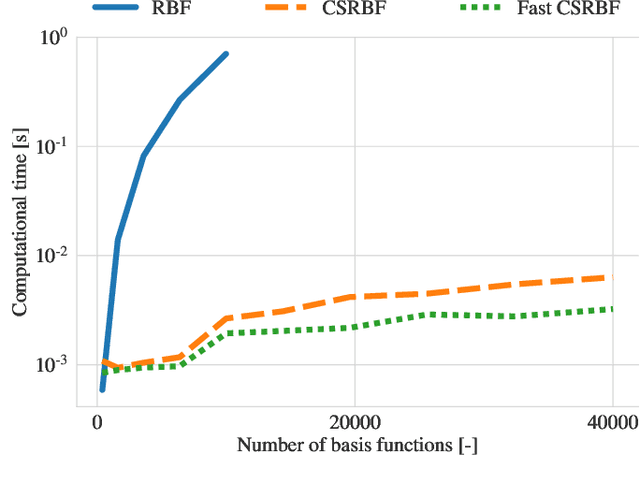
A computationally efficient method for online joint state inference and dynamical model learning is presented. The dynamical model combines an a priori known state-space model with a radial basis function expansion representing unknown system dynamics. Thus, the model is inherently adaptive and can learn unknown and changing system dynamics on-the-fly. Still, by including prior knowledge in the model description, a minimum of estimation performance can be guaranteed already from the start, which is of utmost importance in, e.g., safety-critical applications. The method uses an extended Kalman filter approach to jointly estimate the state of the system and learn the system properties, via the parameters of the basis function expansion. By using compact radial basis functions and an approximate Kalman gain, the computational complexity is considerably reduced compared to similar approaches. The approximation works well when the system dynamics exhibit limited correlation between points well separated in the state-space domain. The method is exemplified via two intelligent vehicle applications where it is shown to: (i) have essentially identical system dynamics estimation performance compared to similar non-real-time algorithms, and (ii) be real-time applicable to large-scale problems.