Composing Flow-Matching Energies with Known Physics: Generation, OOD Detection, and Inversion on PDE Fields

Probabilistic modeling of physical fields benefits from both a data-driven prior and known physical structure such as the governing equations. Energy-based models (EBMs) are a natural fit since energies compose additively, which enables augmenting physics information during inference. However, EBMs have been difficult to train and sample from due to the intractable partition function. We show in this work that flow matching models with a potential-induced velocity yield an explicit scalar energy at all transport times, whose gradient is exactly the converted learned score and which recovers the marginal negative log-density at the population optimum. The time-dependent energy functions are obtained purely from the matching regression objective on an independent linear Gaussian interpolation, without a variational form or additional MCMC steps, and the sampling retains the flow ODE. Access to the energy function from a trained model serves three roles: energy-corrected data generation, energy as a scoring function for out-of-distribution (OOD) detection, and energy compositional posterior sampling for inverse problems. In particular, we show the explicit energy permits general MCMC samplers in the predictor-corrector sampling framework, reducing PDE residual and spectral distance compared to the flow ODE baseline. Furthermore, we demonstrate utilizing the data energy and physics-based energy (e.g., PDE residuals) as complementary mechanisms to improve detection accuracy for OOD tasks. In addition, we explore the connection to MCMC-based inference for inverse problems by composing the energy with a quadratic observational likelihood that yields a posterior energy, used as an explicitly chosen family of inference-time targets.

Multi-task Modeling for Engineering Applications with Sparse Data

Modern engineering and scientific workflows often require simultaneous predictions across related tasks and fidelity levels, where high-fidelity data is scarce and expensive, while low-fidelity data is more abundant. This paper introduces an Multi-Task Gaussian Processes (MTGP) framework tailored for engineering systems characterized by multi-source, multi-fidelity data, addressing challenges of data sparsity and varying task correlations. The proposed framework leverages inter-task relationships across outputs and fidelity levels to improve predictive performance and reduce computational costs. The framework is validated across three representative scenarios: Forrester function benchmark, 3D ellipsoidal void modeling, and friction-stir welding. By quantifying and leveraging inter-task relationships, the proposed MTGP framework offers a robust and scalable solution for predictive modeling in domains with significant computational and experimental costs, supporting informed decision-making and efficient resource utilization.

Efficient Flow Matching using Latent Variables

Flow matching models have shown great potential in image generation tasks among probabilistic generative models. Building upon the ideas of continuous normalizing flows, flow matching models generalize the transport path of the diffusion models from a simple prior distribution to the data. Most flow matching models in the literature do not explicitly model the underlying structure/manifold in the target data when learning the flow from a simple source distribution like the standard Gaussian. This leads to inefficient learning, especially for many high-dimensional real-world datasets, which often reside in a low-dimensional manifold. Existing strategies of incorporating manifolds, including data with underlying multi-modal distribution, often require expensive training and hence frequently lead to suboptimal performance. To this end, we present \texttt{Latent-CFM}, which provides simplified training/inference strategies to incorporate multi-modal data structures using pretrained deep latent variable models. Through experiments on multi-modal synthetic data and widely used image benchmark datasets, we show that \texttt{Latent-CFM} exhibits improved generation quality with significantly less training ($\sim 50\%$ less in some cases) and computation than state-of-the-art flow matching models. Using a 2d Darcy flow dataset, we demonstrate that our approach generates more physically accurate samples than competitive approaches. In addition, through latent space analysis, we demonstrate that our approach can be used for conditional image generation conditioned on latent features.

REMEDI: Corrective Transformations for Improved Neural Entropy Estimation

Information theoretic quantities play a central role in machine learning. The recent surge in the complexity of data and models has increased the demand for accurate estimation of these quantities. However, as the dimension grows the estimation presents significant challenges, with existing methods struggling already in relatively low dimensions. To address this issue, in this work, we introduce $\texttt{REMEDI}$ for efficient and accurate estimation of differential entropy, a fundamental information theoretic quantity. The approach combines the minimization of the cross-entropy for simple, adaptive base models and the estimation of their deviation, in terms of the relative entropy, from the data density. Our approach demonstrates improvement across a broad spectrum of estimation tasks, encompassing entropy estimation on both synthetic and natural data. Further, we extend important theoretical consistency results to a more generalized setting required by our approach. We illustrate how the framework can be naturally extended to information theoretic supervised learning models, with a specific focus on the Information Bottleneck approach. It is demonstrated that the method delivers better accuracy compared to the existing methods in Information Bottleneck. In addition, we explore a natural connection between $\texttt{REMEDI}$ and generative modeling using rejection sampling and Langevin dynamics.

Sparsity-Inducing Categorical Prior Improves Robustness of the Information Bottleneck

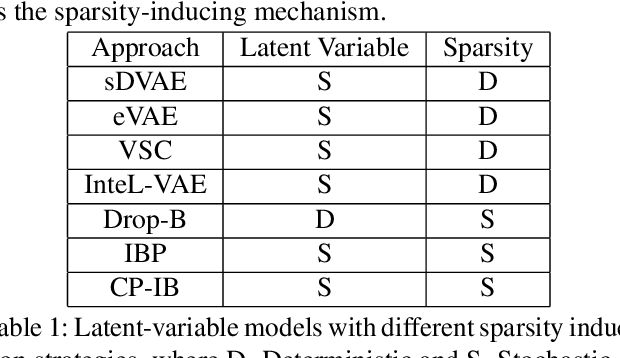
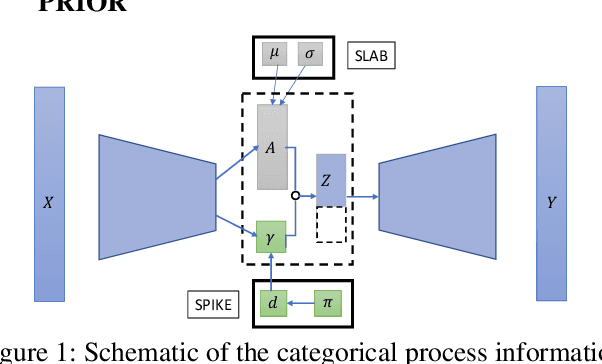
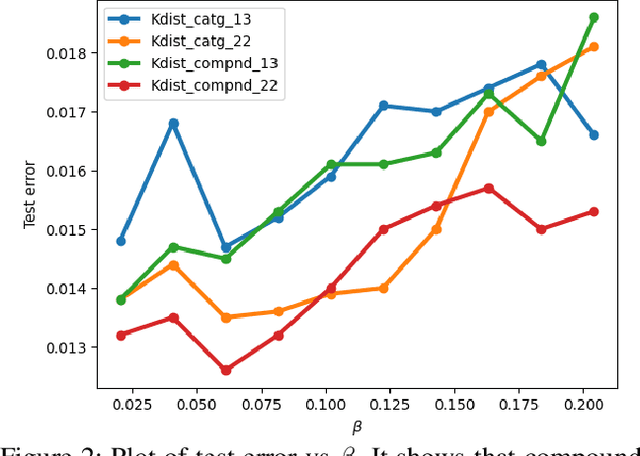
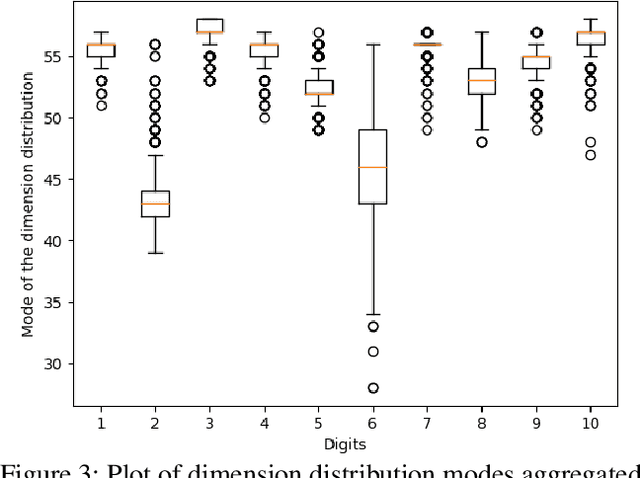
The information bottleneck framework provides a systematic approach to learn representations that compress nuisance information in inputs and extract semantically meaningful information about the predictions. However, the choice of the prior distribution that fix the dimensionality across all the data can restrict the flexibility of this approach to learn robust representations. We present a novel sparsity-inducing spike-slab prior that uses sparsity as a mechanism to provide flexibility that allows each data point to learn its own dimension distribution. In addition, it provides a mechanism to learn a joint distribution of the latent variable and the sparsity. Thus, unlike other approaches, it can account for the full uncertainty in the latent space. Through a series of experiments using in-distribution and out-of-distribution learning scenarios on the MNIST and Fashion-MNIST data we show that the proposed approach improves the accuracy and robustness compared with the traditional fixed -imensional priors as well as other sparsity-induction mechanisms proposed in the literature.