Learning Equilibria in Matching Games with Bandit Feedback

We investigate the problem of learning an equilibrium in a generalized two-sided matching market, where agents can adaptively choose their actions based on their assigned matches. Specifically, we consider a setting in which matched agents engage in a zero-sum game with initially unknown payoff matrices, and we explore whether a centralized procedure can learn an equilibrium from bandit feedback. We adopt the solution concept of matching equilibrium, where a pair consisting of a matching $\mathfrak{m}$ and a set of agent strategies $X$ forms an equilibrium if no agent has the incentive to deviate from $(\mathfrak{m}, X)$. To measure the deviation of a given pair $(\mathfrak{m}, X)$ from the equilibrium pair $(\mathfrak{m}^\star, X^\star)$, we introduce matching instability that can serve as a regret measure for the corresponding learning problem. We then propose a UCB algorithm in which agents form preferences and select actions based on optimistic estimates of the game payoffs, and prove that it achieves sublinear, instance-independent regret over a time horizon $T$.

Probably Correct Optimal Stable Matching for Two-Sided Markets Under Uncertainty

We consider a learning problem for the stable marriage model under unknown preferences for the left side of the market. We focus on the centralized case, where at each time step, an online platform matches the agents, and obtains a noisy evaluation reflecting their preferences. Our aim is to quickly identify the stable matching that is left-side optimal, rendering this a pure exploration problem with bandit feedback. We specifically aim to find Probably Correct Optimal Stable Matchings and present several bandit algorithms to do so. Our findings provide a foundational understanding of how to efficiently gather and utilize preference information to identify the optimal stable matching in two-sided markets under uncertainty. An experimental analysis on synthetic data complements theoretical results on sample complexities for the proposed methods.

Shifts 2.0: Extending The Dataset of Real Distributional Shifts

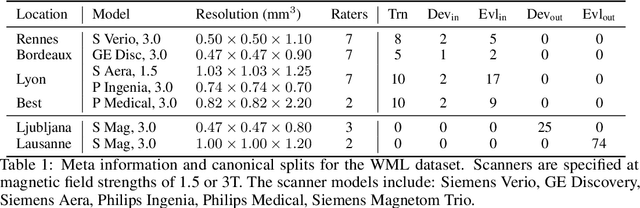
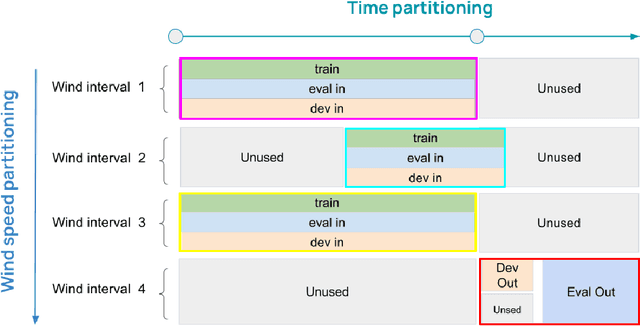
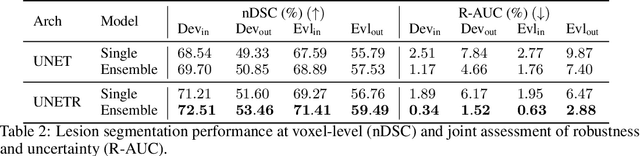
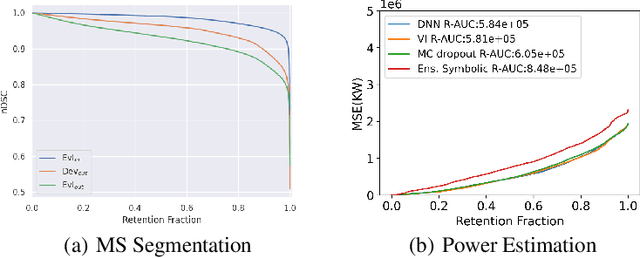
Distributional shift, or the mismatch between training and deployment data, is a significant obstacle to the usage of machine learning in high-stakes industrial applications, such as autonomous driving and medicine. This creates a need to be able to assess how robustly ML models generalize as well as the quality of their uncertainty estimates. Standard ML baseline datasets do not allow these properties to be assessed, as the training, validation and test data are often identically distributed. Recently, a range of dedicated benchmarks have appeared, featuring both distributionally matched and shifted data. Among these benchmarks, the Shifts dataset stands out in terms of the diversity of tasks as well as the data modalities it features. While most of the benchmarks are heavily dominated by 2D image classification tasks, Shifts contains tabular weather forecasting, machine translation, and vehicle motion prediction tasks. This enables the robustness properties of models to be assessed on a diverse set of industrial-scale tasks and either universal or directly applicable task-specific conclusions to be reached. In this paper, we extend the Shifts Dataset with two datasets sourced from industrial, high-risk applications of high societal importance. Specifically, we consider the tasks of segmentation of white matter Multiple Sclerosis lesions in 3D magnetic resonance brain images and the estimation of power consumption in marine cargo vessels. Both tasks feature ubiquitous distributional shifts and a strict safety requirement due to the high cost of errors. These new datasets will allow researchers to further explore robust generalization and uncertainty estimation in new situations. In this work, we provide a description of the dataset and baseline results for both tasks.