Efficient Per-Example Gradient Computations in Convolutional Neural Networks

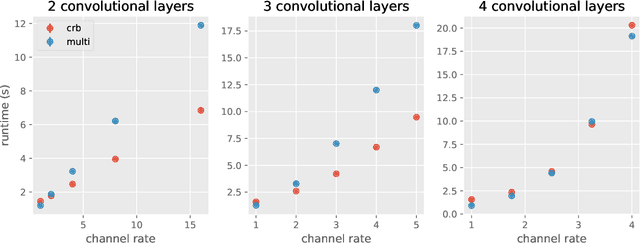
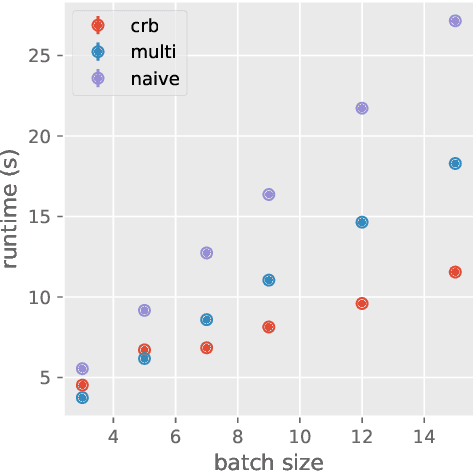
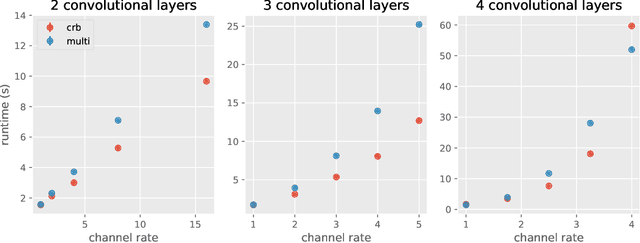
Deep learning frameworks leverage GPUs to perform massively-parallel computations over batches of many training examples efficiently. However, for certain tasks, one may be interested in performing per-example computations, for instance using per-example gradients to evaluate a quantity of interest unique to each example. One notable application comes from the field of differential privacy, where per-example gradients must be norm-bounded in order to limit the impact of each example on the aggregated batch gradient. In this work, we discuss how per-example gradients can be efficiently computed in convolutional neural networks (CNNs). We compare existing strategies by performing a few steps of differentially-private training on CNNs of varying sizes. We also introduce a new strategy for per-example gradient calculation, which is shown to be advantageous depending on the model architecture and how the model is trained. This is a first step in making differentially-private training of CNNs practical.

Entropy and mutual information in models of deep neural networks

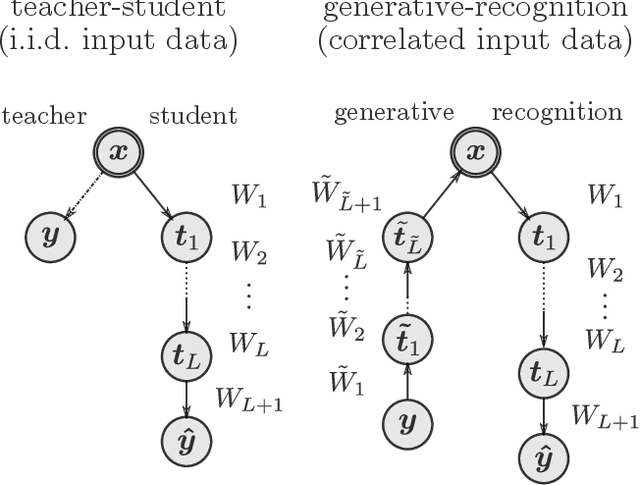
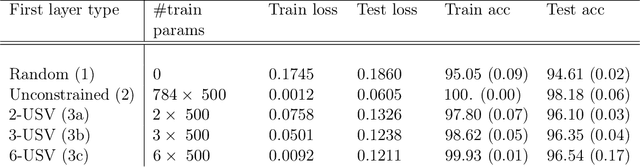
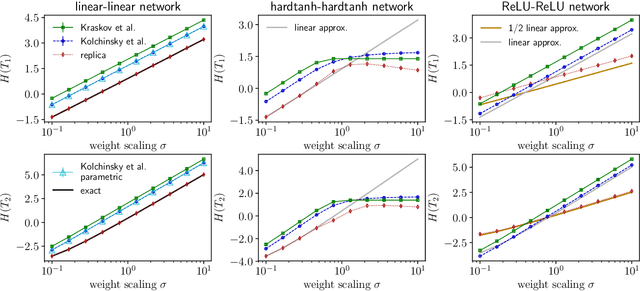
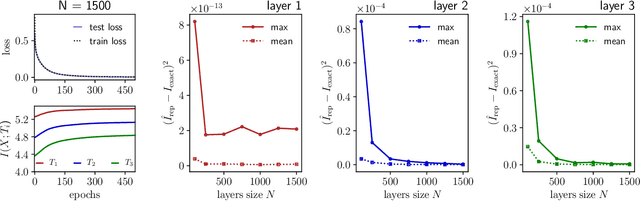
We examine a class of deep learning models with a tractable method to compute information-theoretic quantities. Our contributions are three-fold: (i) We show how entropies and mutual informations can be derived from heuristic statistical physics methods, under the assumption that weight matrices are independent and orthogonally-invariant. (ii) We extend particular cases in which this result is known to be rigorously exact by providing a proof for two-layers networks with Gaussian random weights, using the recently introduced adaptive interpolation method. (iii) We propose an experiment framework with generative models of synthetic datasets, on which we train deep neural networks with a weight constraint designed so that the assumption in (i) is verified during learning. We study the behavior of entropies and mutual informations throughout learning and conclude that, in the proposed setting, the relationship between compression and generalization remains elusive.

Approximate message-passing for convex optimization with non-separable penalties

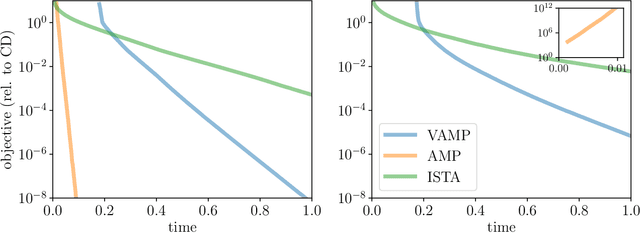
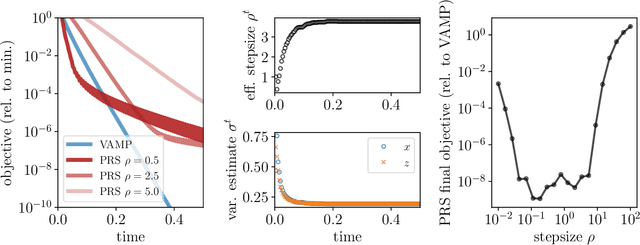
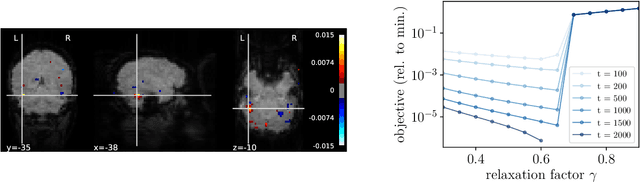
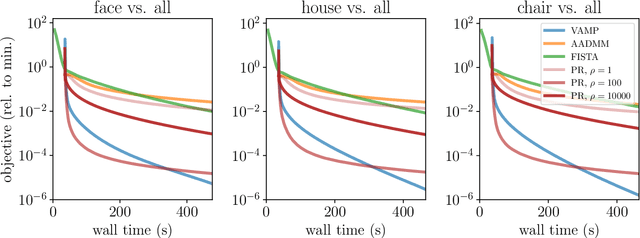
We introduce an iterative optimization scheme for convex objectives consisting of a linear loss and a non-separable penalty, based on the expectation-consistent approximation and the vector approximate message-passing (VAMP) algorithm. Specifically, the penalties we approach are convex on a linear transformation of the variable to be determined, a notable example being total variation (TV). We describe the connection between message-passing algorithms -- typically used for approximate inference -- and proximal methods for optimization, and show that our scheme is, as VAMP, similar in nature to the Peaceman-Rachford splitting, with the important difference that stepsizes are set adaptively. Finally, we benchmark the performance of our VAMP-like iteration in problems where TV penalties are useful, namely classification in task fMRI and reconstruction in tomography, and show faster convergence than that of state-of-the-art approaches such as FISTA and ADMM in most settings.

Streaming Bayesian inference: theoretical limits and mini-batch approximate message-passing

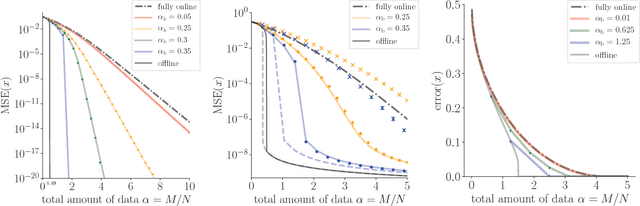
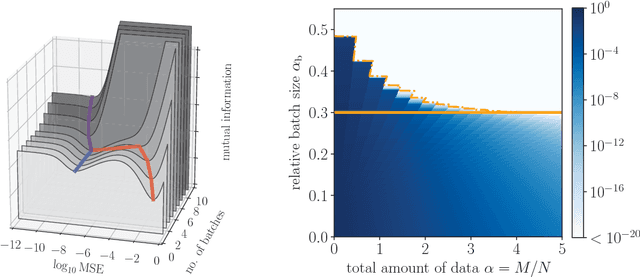
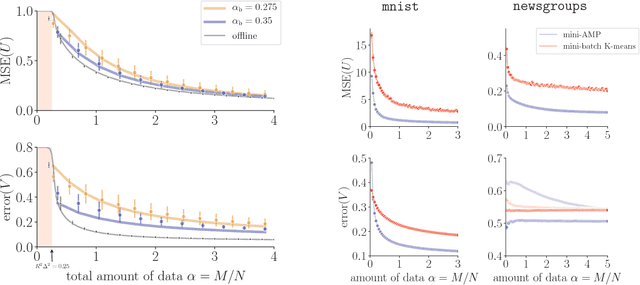
In statistical learning for real-world large-scale data problems, one must often resort to "streaming" algorithms which operate sequentially on small batches of data. In this work, we present an analysis of the information-theoretic limits of mini-batch inference in the context of generalized linear models and low-rank matrix factorization. In a controlled Bayes-optimal setting, we characterize the optimal performance and phase transitions as a function of mini-batch size. We base part of our results on a detailed analysis of a mini-batch version of the approximate message-passing algorithm (Mini-AMP), which we introduce. Additionally, we show that this theoretical optimality carries over into real-data problems by illustrating that Mini-AMP is competitive with standard streaming algorithms for clustering.

Multi-Layer Generalized Linear Estimation

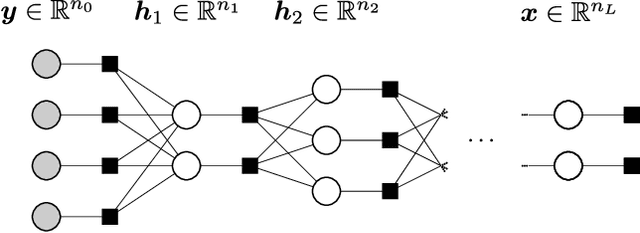
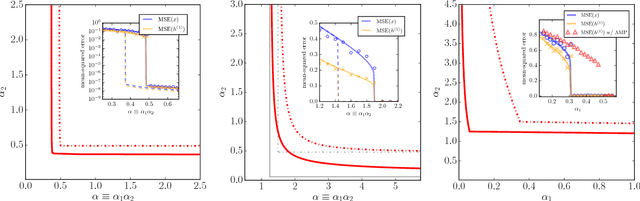
We consider the problem of reconstructing a signal from multi-layered (possibly) non-linear measurements. Using non-rigorous but standard methods from statistical physics we present the Multi-Layer Approximate Message Passing (ML-AMP) algorithm for computing marginal probabilities of the corresponding estimation problem and derive the associated state evolution equations to analyze its performance. We also give the expression of the asymptotic free energy and the minimal information-theoretically achievable reconstruction error. Finally, we present some applications of this measurement model for compressed sensing and perceptron learning with structured matrices/patterns, and for a simple model of estimation of latent variables in an auto-encoder.

Inferring Sparsity: Compressed Sensing using Generalized Restricted Boltzmann Machines

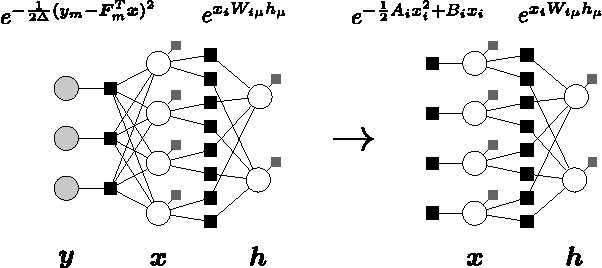
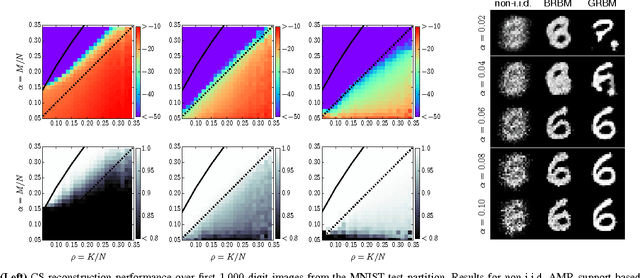
In this work, we consider compressed sensing reconstruction from $M$ measurements of $K$-sparse structured signals which do not possess a writable correlation model. Assuming that a generative statistical model, such as a Boltzmann machine, can be trained in an unsupervised manner on example signals, we demonstrate how this signal model can be used within a Bayesian framework of signal reconstruction. By deriving a message-passing inference for general distribution restricted Boltzmann machines, we are able to integrate these inferred signal models into approximate message passing for compressed sensing reconstruction. Finally, we show for the MNIST dataset that this approach can be very effective, even for $M < K$.

Expectation Propagation

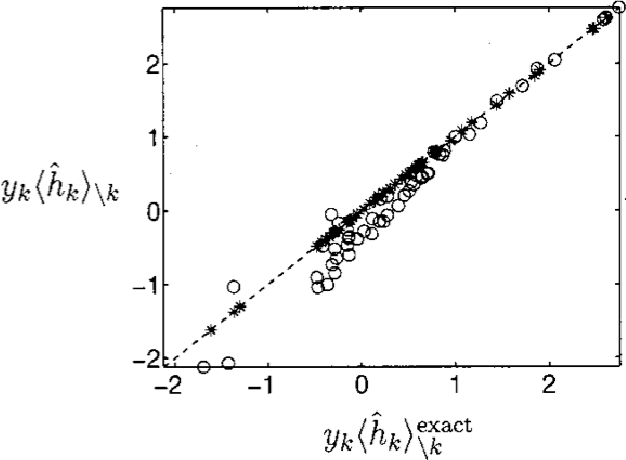
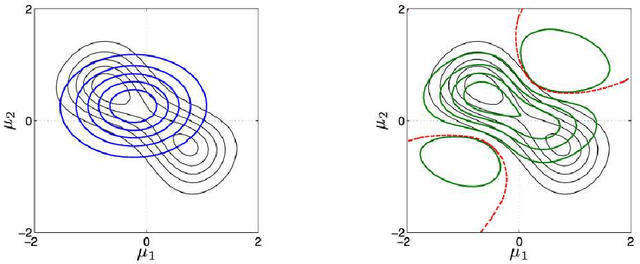
Variational inference is a powerful concept that underlies many iterative approximation algorithms; expectation propagation, mean-field methods and belief propagations were all central themes at the school that can be perceived from this unifying framework. The lectures of Manfred Opper introduce the archetypal example of Expectation Propagation, before establishing the connection with the other approximation methods. Corrections by expansion about the expectation propagation are then explained. Finally some advanced inference topics and applications are explored in the final sections.

Sparse Estimation with the Swept Approximated Message-Passing Algorithm

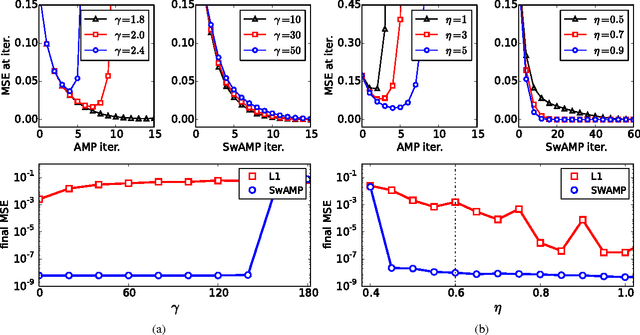
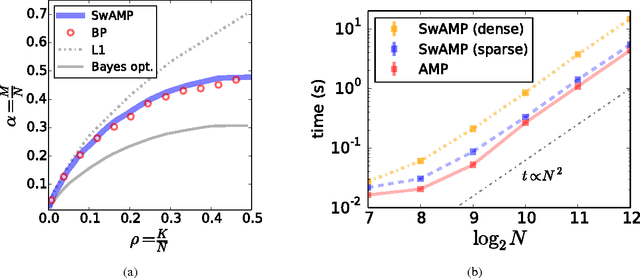
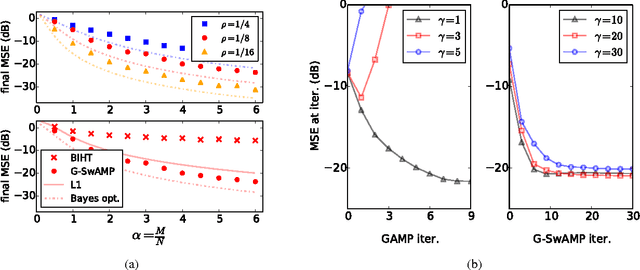
Approximate Message Passing (AMP) has been shown to be a superior method for inference problems, such as the recovery of signals from sets of noisy, lower-dimensionality measurements, both in terms of reconstruction accuracy and in computational efficiency. However, AMP suffers from serious convergence issues in contexts that do not exactly match its assumptions. We propose a new approach to stabilizing AMP in these contexts by applying AMP updates to individual coefficients rather than in parallel. Our results show that this change to the AMP iteration can provide theoretically expected, but hitherto unobtainable, performance for problems on which the standard AMP iteration diverges. Additionally, we find that the computational costs of this swept coefficient update scheme is not unduly burdensome, allowing it to be applied efficiently to signals of large dimensionality.