André F. T. Martins
Quality-Aware Decoding for Neural Machine Translation
May 02, 2022
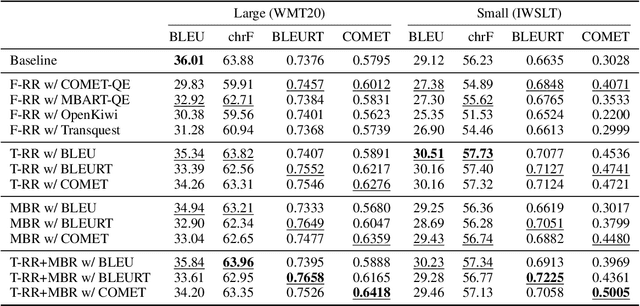
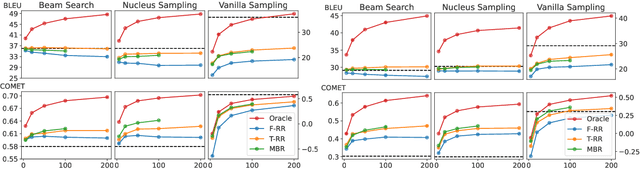
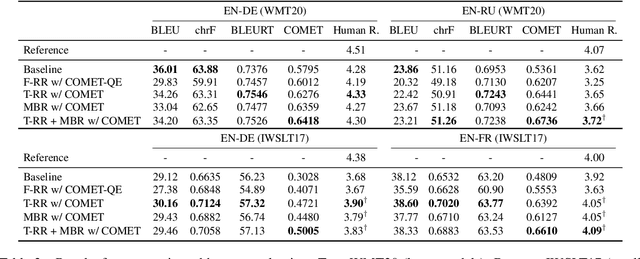
Abstract:Despite the progress in machine translation quality estimation and evaluation in the last years, decoding in neural machine translation (NMT) is mostly oblivious to this and centers around finding the most probable translation according to the model (MAP decoding), approximated with beam search. In this paper, we bring together these two lines of research and propose quality-aware decoding for NMT, by leveraging recent breakthroughs in reference-free and reference-based MT evaluation through various inference methods like $N$-best reranking and minimum Bayes risk decoding. We perform an extensive comparison of various possible candidate generation and ranking methods across four datasets and two model classes and find that quality-aware decoding consistently outperforms MAP-based decoding according both to state-of-the-art automatic metrics (COMET and BLEURT) and to human assessments. Our code is available at https://github.com/deep-spin/qaware-decode.
Efficient Machine Translation Domain Adaptation
Apr 26, 2022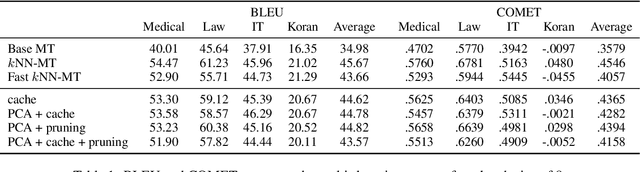
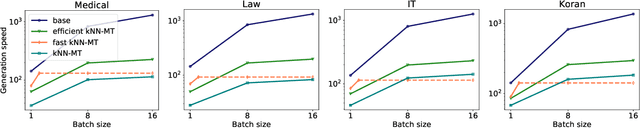
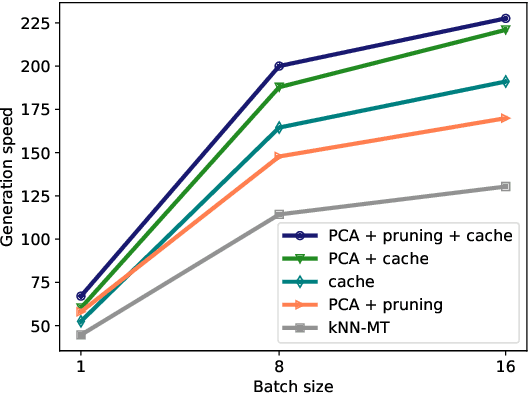
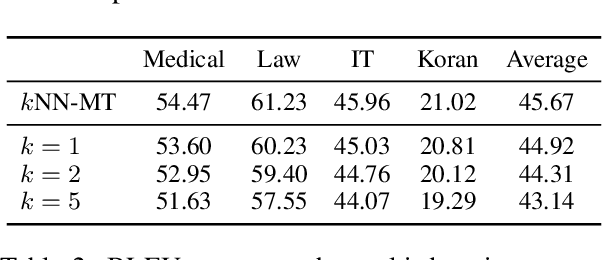
Abstract:Machine translation models struggle when translating out-of-domain text, which makes domain adaptation a topic of critical importance. However, most domain adaptation methods focus on fine-tuning or training the entire or part of the model on every new domain, which can be costly. On the other hand, semi-parametric models have been shown to successfully perform domain adaptation by retrieving examples from an in-domain datastore (Khandelwal et al., 2021). A drawback of these retrieval-augmented models, however, is that they tend to be substantially slower. In this paper, we explore several approaches to speed up nearest neighbor machine translation. We adapt the methods recently proposed by He et al. (2021) for language modeling, and introduce a simple but effective caching strategy that avoids performing retrieval when similar contexts have been seen before. Translation quality and runtimes for several domains show the effectiveness of the proposed solutions.
Learning to Scaffold: Optimizing Model Explanations for Teaching
Apr 22, 2022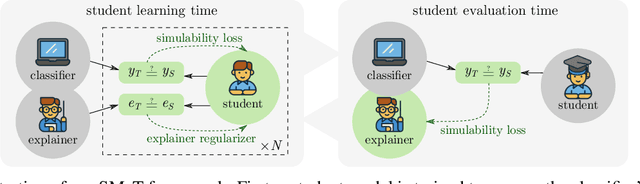
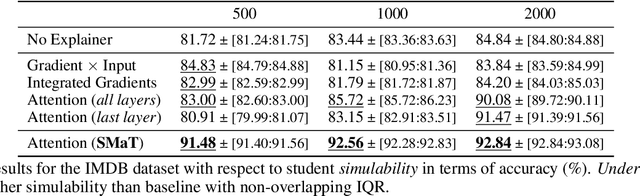
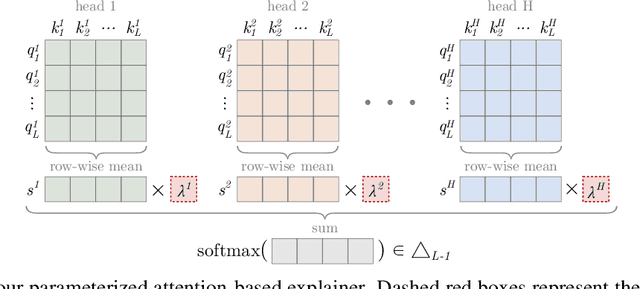

Abstract:Modern machine learning models are opaque, and as a result there is a burgeoning academic subfield on methods that explain these models' behavior. However, what is the precise goal of providing such explanations, and how can we demonstrate that explanations achieve this goal? Some research argues that explanations should help teach a student (either human or machine) to simulate the model being explained, and that the quality of explanations can be measured by the simulation accuracy of students on unexplained examples. In this work, leveraging meta-learning techniques, we extend this idea to improve the quality of the explanations themselves, specifically by optimizing explanations such that student models more effectively learn to simulate the original model. We train models on three natural language processing and computer vision tasks, and find that students trained with explanations extracted with our framework are able to simulate the teacher significantly more effectively than ones produced with previous methods. Through human annotations and a user study, we further find that these learned explanations more closely align with how humans would explain the required decisions in these tasks. Our code is available at https://github.com/coderpat/learning-scaffold
Better Uncertainty Quantification for Machine Translation Evaluation
Apr 13, 2022
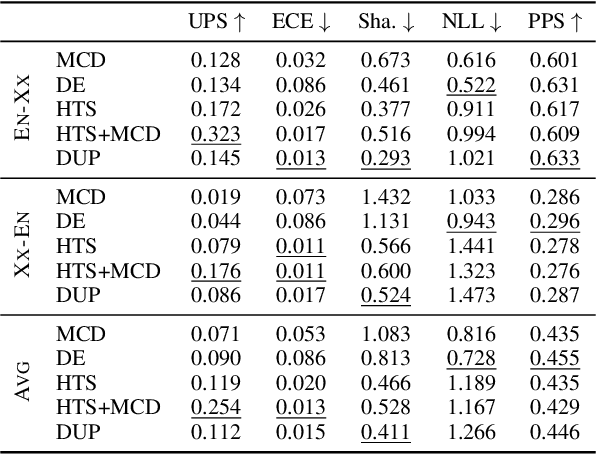

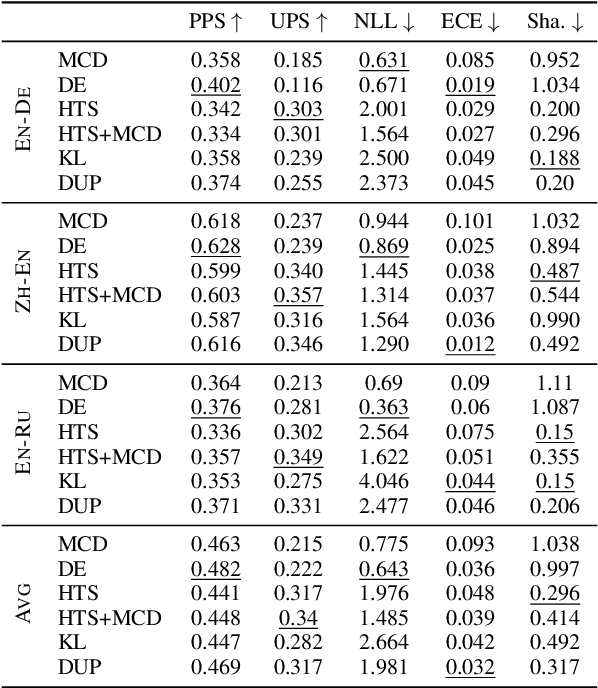
Abstract:Neural-based machine translation (MT) evaluation metrics are progressing fast. However, these systems are often hard to interpret and might produce unreliable scores when human references or assessments are noisy or when data is out-of-domain. Recent work leveraged uncertainty quantification techniques such as Monte Carlo dropout and deep ensembles to provide confidence intervals, but these techniques (as we show) are limited in several ways. In this paper we investigate more powerful and efficient uncertainty predictors for MT evaluation metrics and their potential to capture aleatoric and epistemic uncertainty. To this end we train the COMET metric with new heteroscedastic regression, divergence minimization, and direct uncertainty prediction objectives. Our experiments show improved results on WMT20 and WMT21 metrics task datasets and a substantial reduction in computational costs. Moreover, they demonstrate the ability of our predictors to identify low quality references and to reveal model uncertainty due to out-of-domain data.
Differentiable Causal Discovery Under Latent Interventions
Mar 04, 2022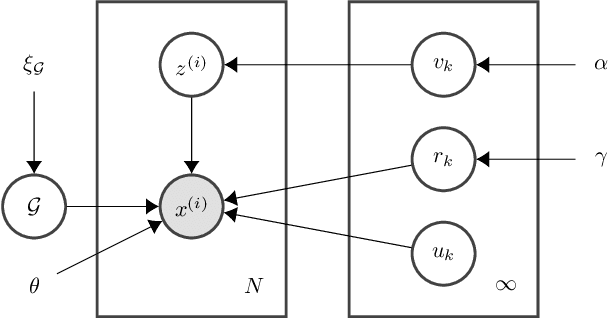
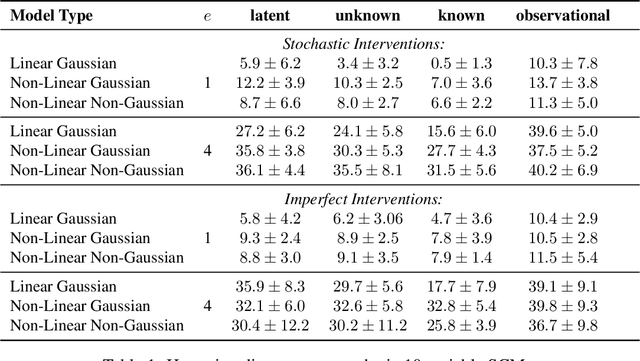
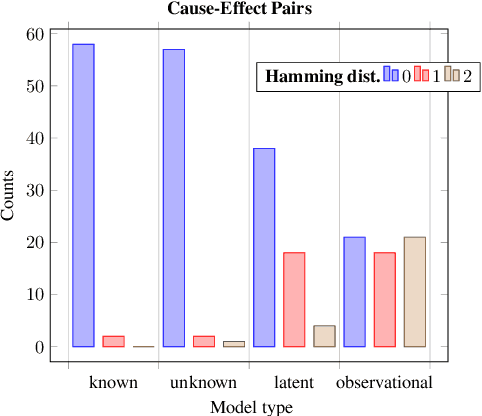
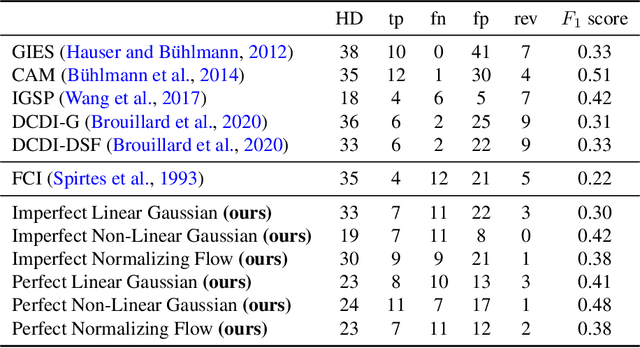
Abstract:Recent work has shown promising results in causal discovery by leveraging interventional data with gradient-based methods, even when the intervened variables are unknown. However, previous work assumes that the correspondence between samples and interventions is known, which is often unrealistic. We envision a scenario with an extensive dataset sampled from multiple intervention distributions and one observation distribution, but where we do not know which distribution originated each sample and how the intervention affected the system, \textit{i.e.}, interventions are entirely latent. We propose a method based on neural networks and variational inference that addresses this scenario by framing it as learning a shared causal graph among an infinite mixture (under a Dirichlet process prior) of intervention structural causal models. Experiments with synthetic and real data show that our approach and its semi-supervised variant are able to discover causal relations in this challenging scenario.
Modeling Structure with Undirected Neural Networks
Feb 08, 2022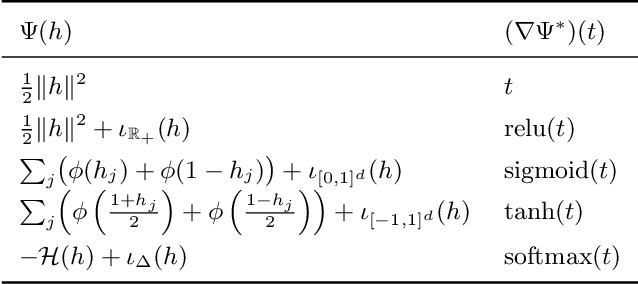
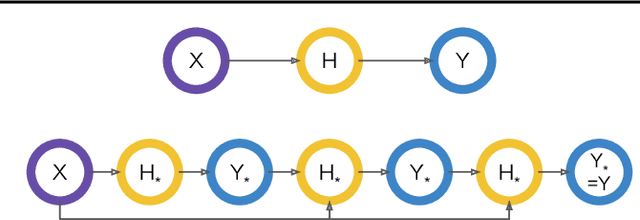

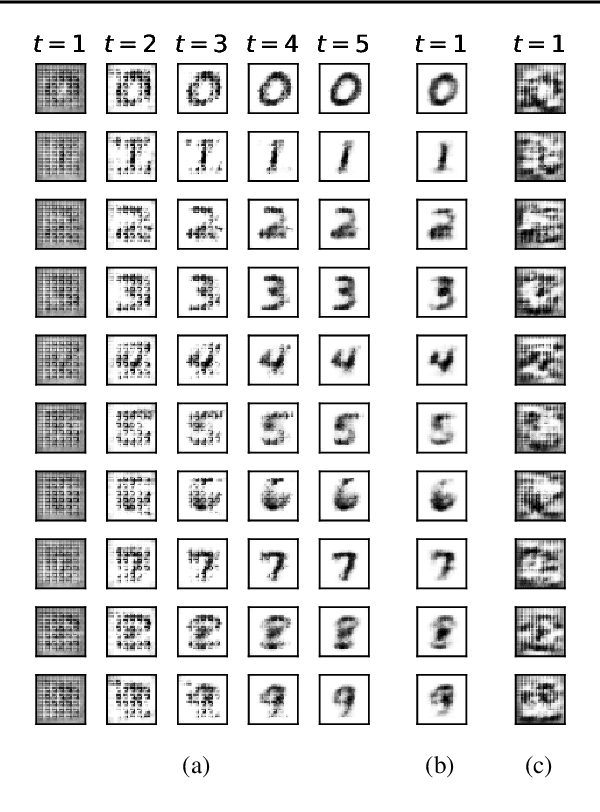
Abstract:Neural networks are powerful function estimators, leading to their status as a paradigm of choice for modeling structured data. However, unlike other structured representations that emphasize the modularity of the problem -- e.g., factor graphs -- neural networks are usually monolithic mappings from inputs to outputs, with a fixed computation order. This limitation prevents them from capturing different directions of computation and interaction between the modeled variables. In this paper, we combine the representational strengths of factor graphs and of neural networks, proposing undirected neural networks (UNNs): a flexible framework for specifying computations that can be performed in any order. For particular choices, our proposed models subsume and extend many existing architectures: feed-forward, recurrent, self-attention networks, auto-encoders, and networks with implicit layers. We demonstrate the effectiveness of undirected neural architectures, both unstructured and structured, on a range of tasks: tree-constrained dependency parsing, convolutional image classification, and sequence completion with attention. By varying the computation order, we show how a single UNN can be used both as a classifier and a prototype generator, and how it can fill in missing parts of an input sequence, making them a promising field for further research.
Predicting Attention Sparsity in Transformers
Sep 24, 2021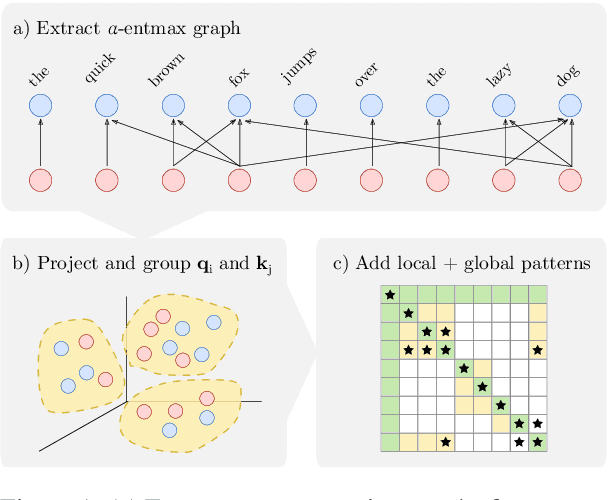
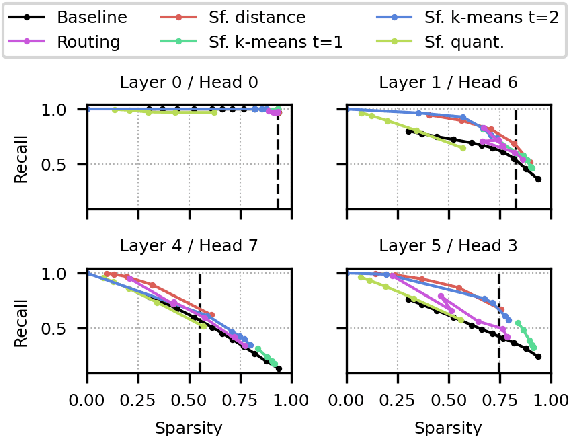

Abstract:A bottleneck in transformer architectures is their quadratic complexity with respect to the input sequence, which has motivated a body of work on efficient sparse approximations to softmax. An alternative path, used by entmax transformers, consists of having built-in exact sparse attention; however this approach still requires quadratic computation. In this paper, we propose Sparsefinder, a simple model trained to identify the sparsity pattern of entmax attention before computing it. We experiment with three variants of our method, based on distances, quantization, and clustering, on two tasks: machine translation (attention in the decoder) and masked language modeling (encoder-only). Our work provides a new angle to study model efficiency by doing extensive analysis of the tradeoff between the sparsity and recall of the predicted attention graph. This allows for detailed comparison between different models, and may guide future benchmarks for sparse models.
When Does Translation Require Context? A Data-driven, Multilingual Exploration
Sep 15, 2021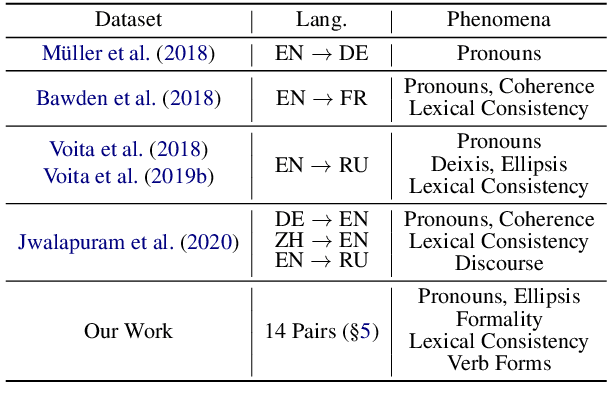
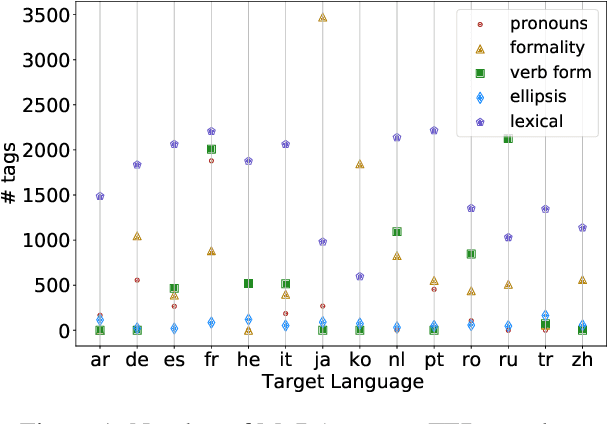

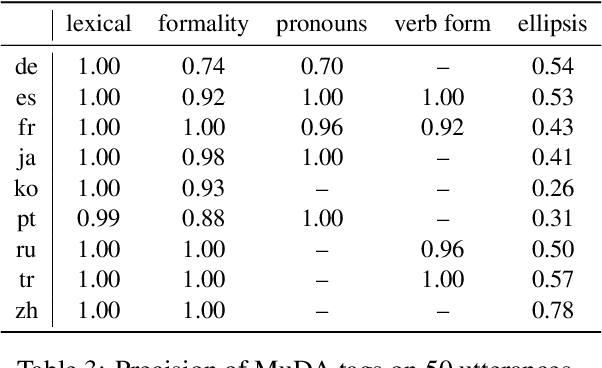
Abstract:Although proper handling of discourse phenomena significantly contributes to the quality of machine translation (MT), common translation quality metrics do not adequately capture them. Recent works in context-aware MT attempt to target a small set of these phenomena during evaluation. In this paper, we propose a new metric, P-CXMI, which allows us to identify translations that require context systematically and confirm the difficulty of previously studied phenomena as well as uncover new ones that have not been addressed in previous work. We then develop the Multilingual Discourse-Aware (MuDA) benchmark, a series of taggers for these phenomena in 14 different language pairs, which we use to evaluate context-aware MT. We find that state-of-the-art context-aware MT models find marginal improvements over context-agnostic models on our benchmark, which suggests current models do not handle these ambiguities effectively. We release code and data to invite the MT research community to increase efforts on context-aware translation on discourse phenomena and languages that are currently overlooked.
$\infty$-former: Infinite Memory Transformer
Sep 15, 2021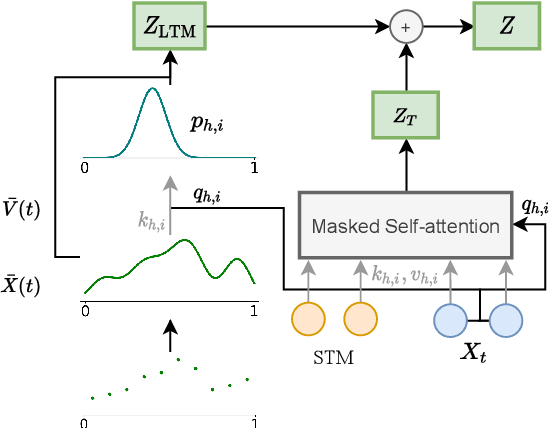

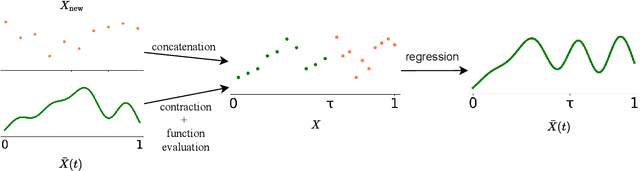

Abstract:Transformers struggle when attending to long contexts, since the amount of computation grows with the context length, and therefore they cannot model long-term memories effectively. Several variations have been proposed to alleviate this problem, but they all have a finite memory capacity, being forced to drop old information. In this paper, we propose the $\infty$-former, which extends the vanilla transformer with an unbounded long-term memory. By making use of a continuous-space attention mechanism to attend over the long-term memory, the $\infty$-former's attention complexity becomes independent of the context length. Thus, it is able to model arbitrarily long contexts and maintain "sticky memories" while keeping a fixed computation budget. Experiments on a synthetic sorting task demonstrate the ability of the $\infty$-former to retain information from long sequences. We also perform experiments on language modeling, by training a model from scratch and by fine-tuning a pre-trained language model, which show benefits of unbounded long-term memories.
Uncertainty-Aware Machine Translation Evaluation
Sep 13, 2021
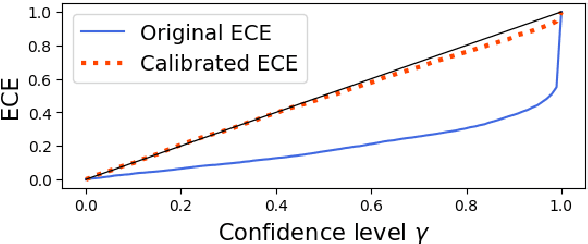
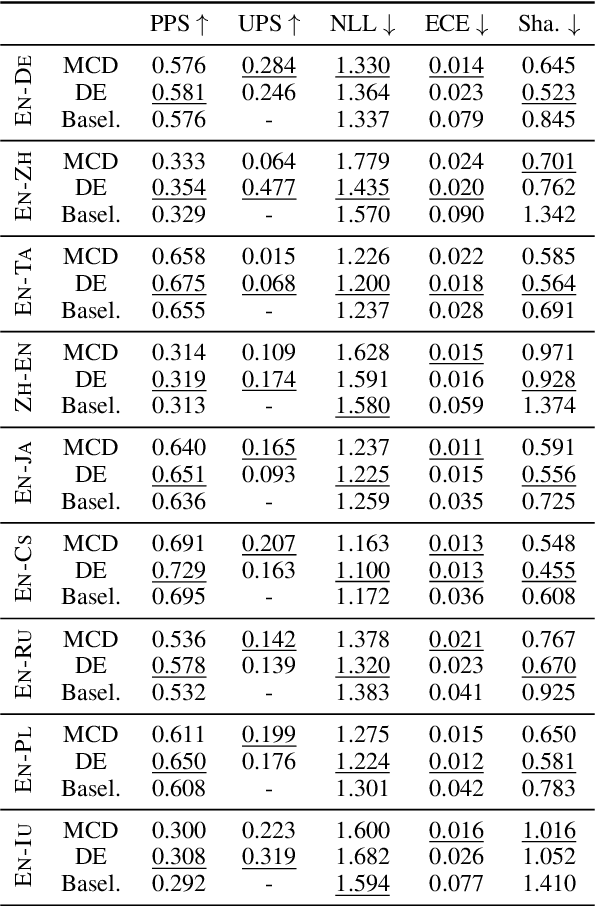
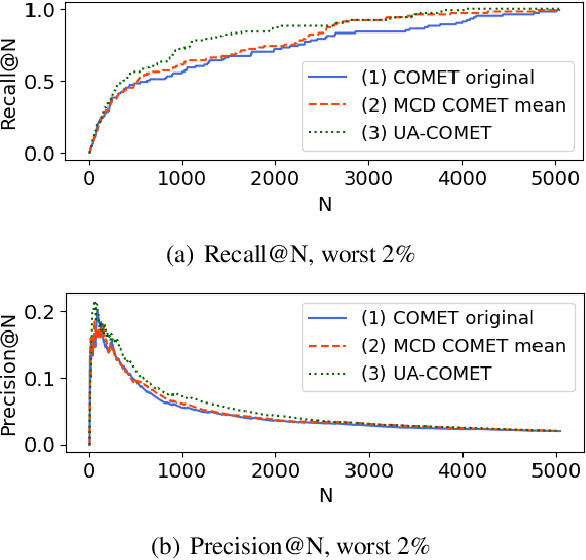
Abstract:Several neural-based metrics have been recently proposed to evaluate machine translation quality. However, all of them resort to point estimates, which provide limited information at segment level. This is made worse as they are trained on noisy, biased and scarce human judgements, often resulting in unreliable quality predictions. In this paper, we introduce uncertainty-aware MT evaluation and analyze the trustworthiness of the predicted quality. We combine the COMET framework with two uncertainty estimation methods, Monte Carlo dropout and deep ensembles, to obtain quality scores along with confidence intervals. We compare the performance of our uncertainty-aware MT evaluation methods across multiple language pairs from the QT21 dataset and the WMT20 metrics task, augmented with MQM annotations. We experiment with varying numbers of references and further discuss the usefulness of uncertainty-aware quality estimation (without references) to flag possibly critical translation mistakes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge