Multi-Agent GraphRAG: A Text-to-Cypher Framework for Labeled Property Graphs

While Retrieval-Augmented Generation (RAG) methods commonly draw information from unstructured documents, the emerging paradigm of GraphRAG aims to leverage structured data such as knowledge graphs. Most existing GraphRAG efforts focus on Resource Description Framework (RDF) knowledge graphs, relying on triple representations and SPARQL queries. However, the potential of Cypher and Labeled Property Graph (LPG) databases to serve as scalable and effective reasoning engines within GraphRAG pipelines remains underexplored in current research literature. To fill this gap, we propose Multi-Agent GraphRAG, a modular LLM agentic system for text-to-Cypher query generation serving as a natural language interface to LPG-based graph data. Our proof-of-concept system features an LLM-based workflow for automated Cypher queries generation and execution, using Memgraph as the graph database backend. Iterative content-aware correction and normalization, reinforced by an aggregated feedback loop, ensures both semantic and syntactic refinement of generated queries. We evaluate our system on the CypherBench graph dataset covering several general domains with diverse types of queries. In addition, we demonstrate performance of the proposed workflow on a property graph derived from the IFC (Industry Foundation Classes) data, representing a digital twin of a building. This highlights how such an approach can bridge AI with real-world applications at scale, enabling industrial digital automation use cases.

Hardware-aware Design of Multiplierless Second-Order IIR Filters with Minimum Adders

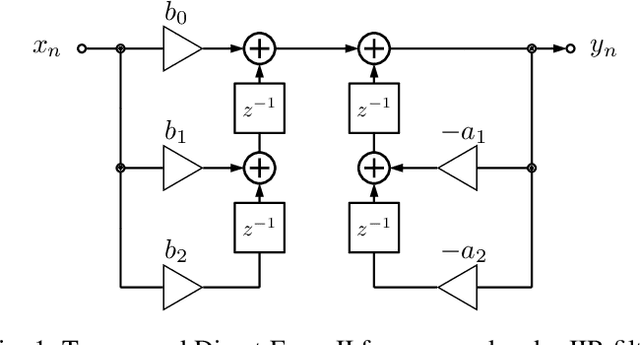
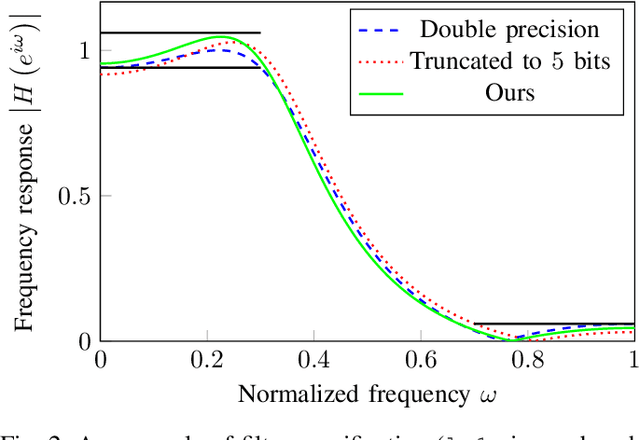
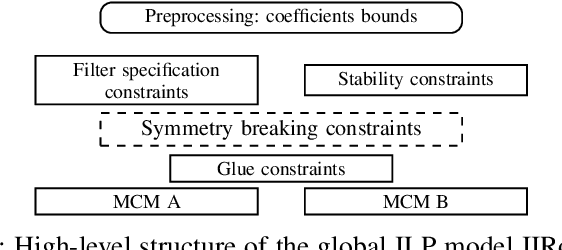
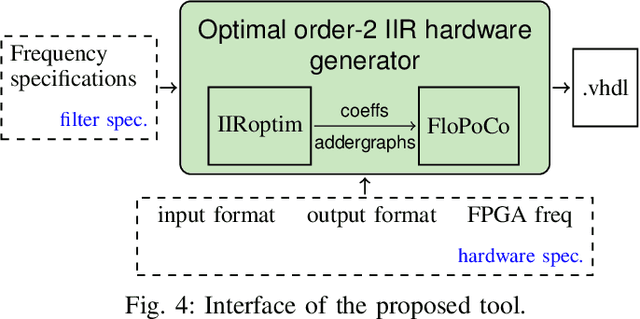
In this work, we optimally solve the problem of multiplierless design of second-order Infinite Impulse Response filters with minimum number of adders. Given a frequency specification, we design a stable direct form filter with hardware-aware fixed-point coefficients that yielding minimal number of adders when replacing all the multiplications by bit shifts and additions. The coefficient design, quantization and implementation, typically conducted independently, are now gathered into one global optimization problem, modeled through integer linear programming and efficiently solved using generic solvers. We guarantee the frequency-domain specifications and stability, which together with optimal number of adders will significantly simplify design-space exploration for filter designers. The optimal filters are implemented within the FloPoCo IP core generator and synthesized for Field Programmable Gate Arrays. With respect to state-of-the-art three-step filter design methods, our one-step design approach achieves, on average, 42% reduction in the number of lookup tables and 21% improvement in delay.

A Framework for Semi-Automatic Precision and Accuracy Analysis for Fast and Rigorous Deep Learning

Deep Neural Networks (DNN) represent a performance-hungry application. Floating-Point (FP) and custom floating-point-like arithmetic satisfies this hunger. While there is need for speed, inference in DNNs does not seem to have any need for precision. Many papers experimentally observe that DNNs can successfully run at almost ridiculously low precision. The aim of this paper is two-fold: first, to shed some theoretical light upon why a DNN's FP accuracy stays high for low FP precision. We observe that the loss of relative accuracy in the convolutional steps is recovered by the activation layers, which are extremely well-conditioned. We give an interpretation for the link between precision and accuracy in DNNs. Second, the paper presents a software framework for semi-automatic FP error analysis for the inference phase of deep-learning. Compatible with common Tensorflow/Keras models, it leverages the frugally-deep Python/C++ library to transform a neural network into C++ code in order to analyze the network's need for precision. This rigorous analysis is based on Interval and Affine arithmetics to compute absolute and relative error bounds for a DNN. We demonstrate our tool with several examples.