Anand Louis
Optimizing Group-Fair Plackett-Luce Ranking Models for Relevance and Ex-Post Fairness
Aug 25, 2023Abstract:In learning-to-rank (LTR), optimizing only the relevance (or the expected ranking utility) can cause representational harm to certain categories of items. Moreover, if there is implicit bias in the relevance scores, LTR models may fail to optimize for true relevance. Previous works have proposed efficient algorithms to train stochastic ranking models that achieve fairness of exposure to the groups ex-ante (or, in expectation), which may not guarantee representation fairness to the groups ex-post, that is, after realizing a ranking from the stochastic ranking model. Typically, ex-post fairness is achieved by post-processing, but previous work does not train stochastic ranking models that are aware of this post-processing. In this paper, we propose a novel objective that maximizes expected relevance only over those rankings that satisfy given representation constraints to ensure ex-post fairness. Building upon recent work on an efficient sampler for ex-post group-fair rankings, we propose a group-fair Plackett-Luce model and show that it can be efficiently optimized for our objective in the LTR framework. Experiments on three real-world datasets show that our group-fair algorithm guarantees fairness alongside usually having better relevance compared to the LTR baselines. In addition, our algorithm also achieves better relevance than post-processing baselines, which also ensures ex-post fairness. Further, when implicit bias is injected into the training data, our algorithm typically outperforms existing LTR baselines in relevance.
Sampling Individually-Fair Rankings that are Always Group Fair
Jun 21, 2023Abstract:Rankings on online platforms help their end-users find the relevant information -- people, news, media, and products -- quickly. Fair ranking tasks, which ask to rank a set of items to maximize utility subject to satisfying group-fairness constraints, have gained significant interest in the Algorithmic Fairness, Information Retrieval, and Machine Learning literature. Recent works, however, identify uncertainty in the utilities of items as a primary cause of unfairness and propose introducing randomness in the output. This randomness is carefully chosen to guarantee an adequate representation of each item (while accounting for the uncertainty). However, due to this randomness, the output rankings may violate group fairness constraints. We give an efficient algorithm that samples rankings from an individually-fair distribution while ensuring that every output ranking is group fair. The expected utility of the output ranking is at least $\alpha$ times the utility of the optimal fair solution. Here, $\alpha$ depends on the utilities, position-discounts, and constraints -- it approaches 1 as the range of utilities or the position-discounts shrinks, or when utilities satisfy distributional assumptions. Empirically, we observe that our algorithm achieves individual and group fairness and that Pareto dominates the state-of-the-art baselines.
Bipartite Matchings with Group Fairness and Individual Fairness Constraints
Aug 23, 2022
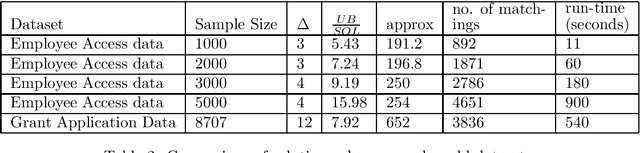
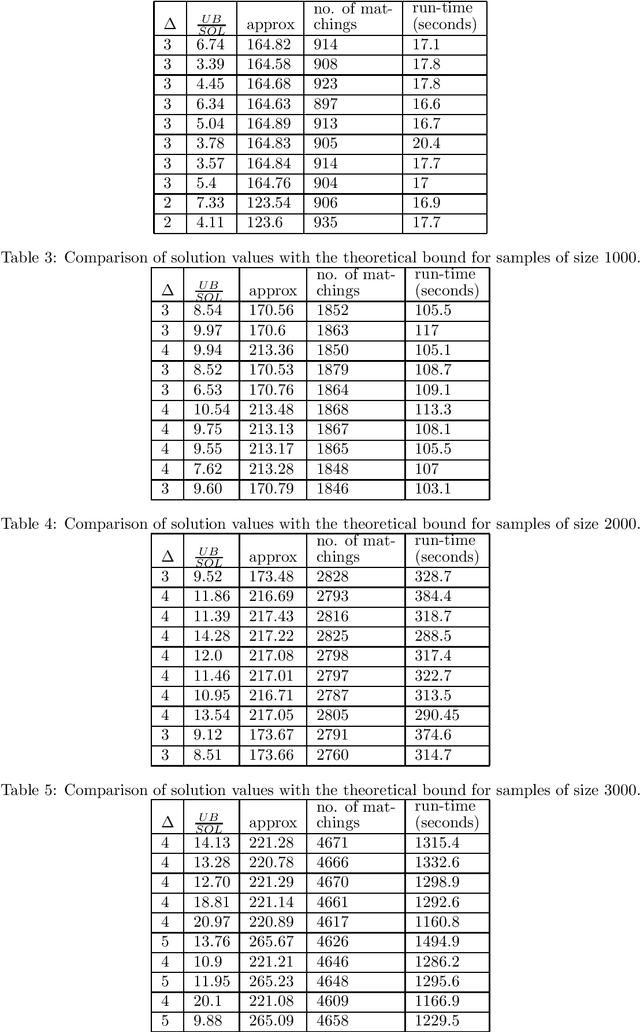
Abstract:We address group as well as individual fairness constraints in matchings in the context of assigning items to platforms. Each item belongs to certain groups and has a preference ordering over platforms. Each platform enforces group fairness by specifying an upper and a lower bound on the number of items that can be matched to it from each group. There could be multiple optimal solutions that satisfy the group fairness constraints. To achieve individual fairness, we introduce `probabilistic individual fairness', where the goal is to compute a distribution over `group fair' matchings such that every item has a reasonable probability of being matched to a platform among its top choices. In the case where each item belongs to exactly one group, we provide a polynomial-time algorithm that computes a probabilistic individually fair distribution over group fair matchings. When an item can belong to multiple groups, and the group fairness constraints are specified as only upper bounds, we rehash the same algorithm to achieve three different polynomial-time approximation algorithms.
Socially Fair Center-based and Linear Subspace Clustering
Aug 22, 2022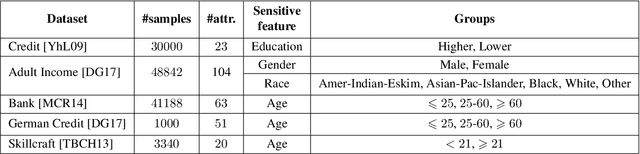
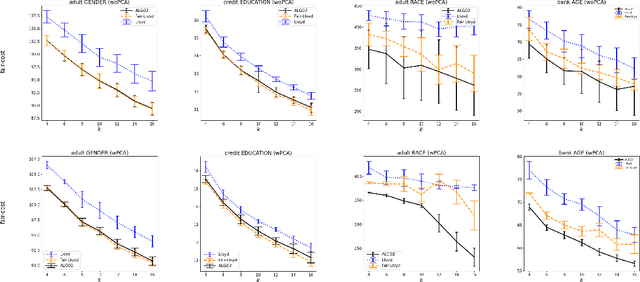
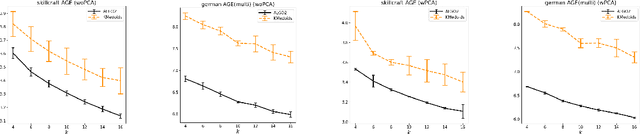
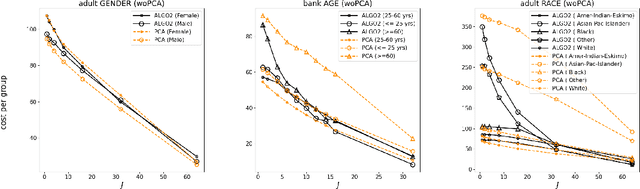
Abstract:Center-based clustering (e.g., $k$-means, $k$-medians) and clustering using linear subspaces are two most popular techniques to partition real-world data into smaller clusters. However, when the data consists of sensitive demographic groups, significantly different clustering cost per point for different sensitive groups can lead to fairness-related harms (e.g., different quality-of-service). The goal of socially fair clustering is to minimize the maximum cost of clustering per point over all groups. In this work, we propose a unified framework to solve socially fair center-based clustering and linear subspace clustering, and give practical, efficient approximation algorithms for these problems. We do extensive experiments to show that on multiple benchmark datasets our algorithms either closely match or outperform state-of-the-art baselines.
Sampling Random Group Fair Rankings
Mar 02, 2022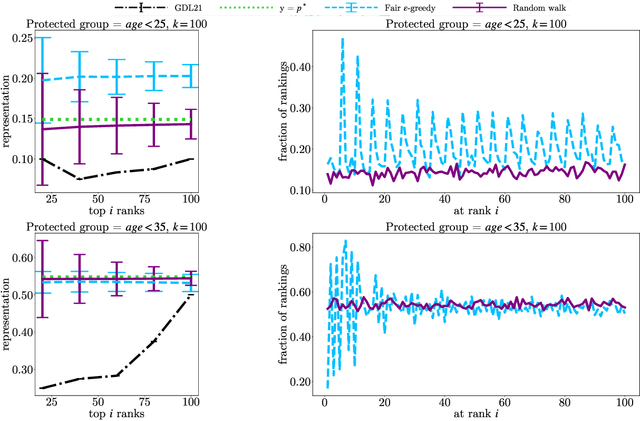
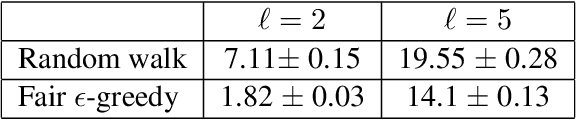
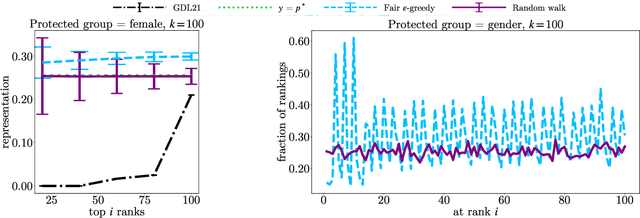
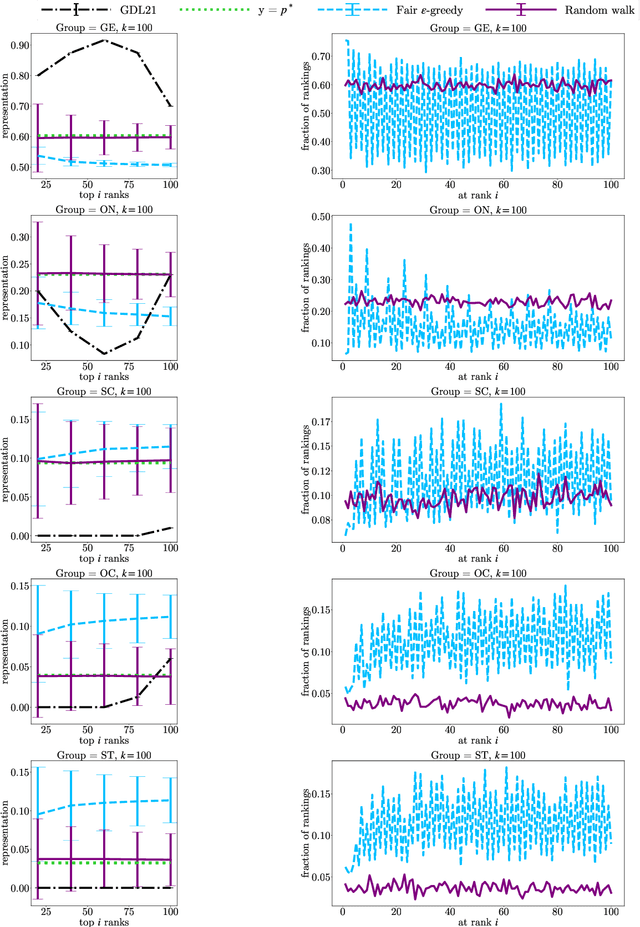
Abstract:In this paper, we consider the problem of randomized group fair ranking that merges given ranked list of items from different sensitive demographic groups while satisfying given lower and upper bounds on the representation of each group in the top ranks. Our randomized group fair ranking formulation works even when there is implicit bias, incomplete relevance information, or when only ordinal ranking is available instead of relevance scores or utility values. We take an axiomatic approach and show that there is a unique distribution $\mathcal{D}$ to sample a random group fair ranking that satisfies a natural set of consistency and fairness axioms. Moreover, $\mathcal{D}$ satisfies representation constraints for every group at every rank, a characteristic that cannot be satisfied by any deterministic ranking. We propose three algorithms to sample a random group fair ranking from $\mathcal{D}$. Our first algorithm samples rankings from $\mathcal{D}$ exactly, in time exponential in the number of groups. Our second algorithm samples random group fair rankings from $\mathcal{D}$ exactly and is faster than the first algorithm when the gap between upper and lower bounds on the representation for each group is small. Our third algorithm samples rankings from a distribution $\epsilon$-close to $\mathcal{D}$ in total variation distance, and has expected running time polynomial in all input parameters and $1/\epsilon$ when there is a large gap between upper and lower bound representation constraints for all the groups. We experimentally validate the above guarantees of our algorithms for group fairness in top ranks and representation in every rank on real-world data sets.
Ranking for Individual and Group Fairness Simultaneously
Sep 24, 2020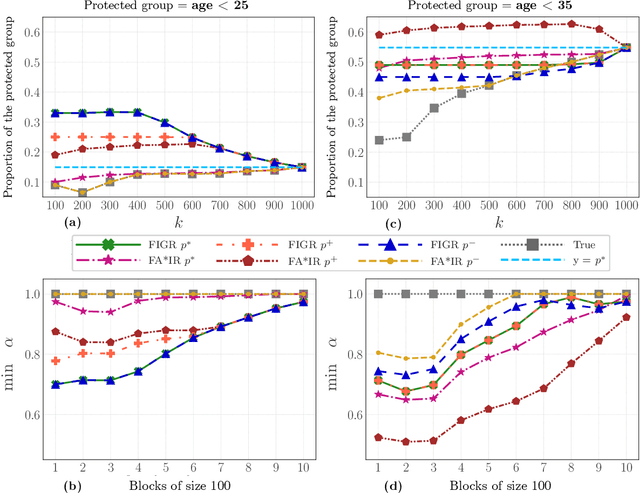
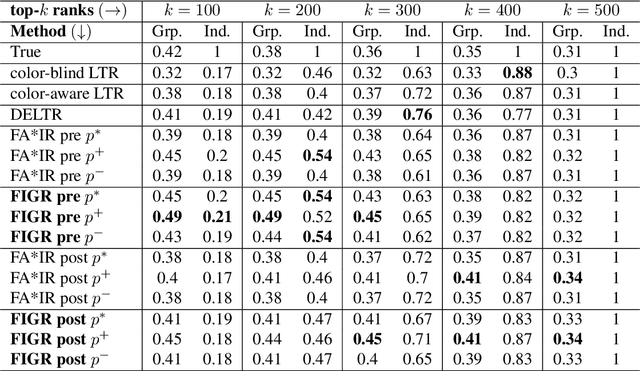
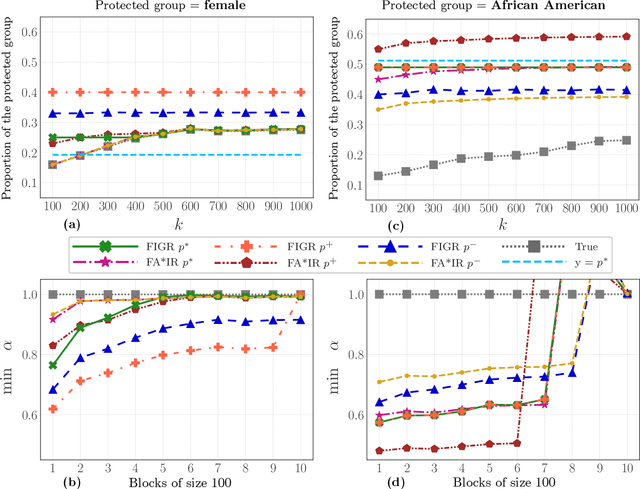
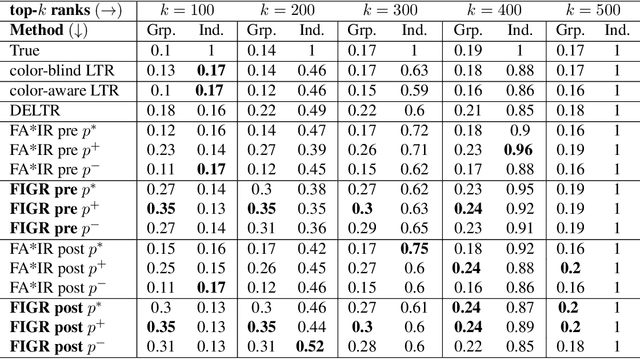
Abstract:Search and recommendation systems, such as search engines, recruiting tools, online marketplaces, news, and social media, output ranked lists of content, products, and sometimes, people. Credit ratings, standardized tests, risk assessments output only a score, but are also used implicitly for ranking. Bias in such ranking systems, especially among the top ranks, can worsen social and economic inequalities, polarize opinions, and reinforce stereotypes. On the other hand, a bias correction for minority groups can cause more harm if perceived as favoring group-fair outcomes over meritocracy. In this paper, we study a trade-off between individual fairness and group fairness in ranking. We define individual fairness based on how close the predicted rank of each item is to its true rank, and prove a lower bound on the trade-off achievable for simultaneous individual and group fairness in ranking. We give a fair ranking algorithm that takes any given ranking and outputs another ranking with simultaneous individual and group fairness guarantees comparable to the lower bound we prove. Our algorithm can be used to both pre-process training data as well as post-process the output of existing ranking algorithms. Our experimental results show that our algorithm performs better than the state-of-the-art fair learning to rank and fair post-processing baselines.
Robust Identifiability in Linear Structural Equation Models of Causal Inference
Jul 14, 2020
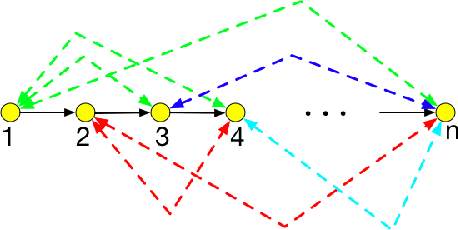
Abstract:In this work, we consider the problem of robust parameter estimation from observational data in the context of linear structural equation models (LSEMs). LSEMs are a popular and well-studied class of models for inferring causality in the natural and social sciences. One of the main problems related to LSEMs is to recover the model parameters from the observational data. Under various conditions on LSEMs and the model parameters the prior work provides efficient algorithms to recover the parameters. However, these results are often about generic identifiability. In practice, generic identifiability is not sufficient and we need robust identifiability: small changes in the observational data should not affect the parameters by a huge amount. Robust identifiability has received far less attention and remains poorly understood. Sankararaman et al. (2019) recently provided a set of sufficient conditions on parameters under which robust identifiability is feasible. However, a limitation of their work is that their results only apply to a small sub-class of LSEMs, called ``bow-free paths.'' In this work, we significantly extend their work along multiple dimensions. First, for a large and well-studied class of LSEMs, namely ``bow free'' models, we provide a sufficient condition on model parameters under which robust identifiability holds, thereby removing the restriction of paths required by prior work. We then show that this sufficient condition holds with high probability which implies that for a large set of parameters robust identifiability holds and that for such parameters, existing algorithms already achieve robust identifiability. Finally, we validate our results on both simulated and real-world datasets.
Stability of Linear Structural Equation Models of Causal Inference
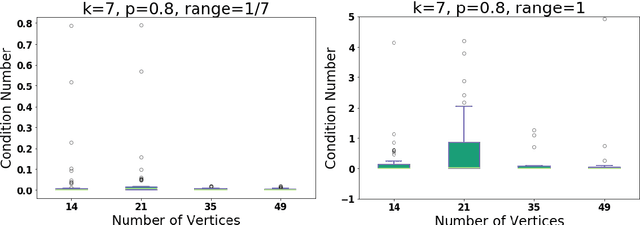
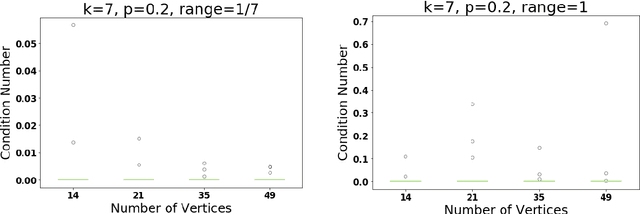
May 16, 2019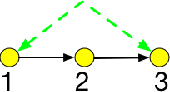
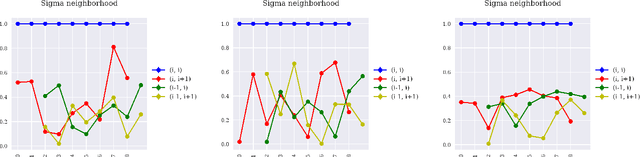

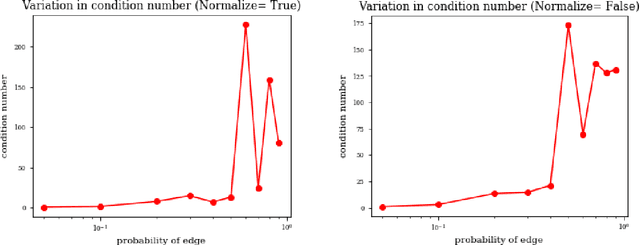
Abstract:We consider the numerical stability of the parameter recovery problem in Linear Structural Equation Model ($\LSEM$) of causal inference. A long line of work starting from Wright (1920) has focused on understanding which sub-classes of $\LSEM$ allow for efficient parameter recovery. Despite decades of study, this question is not yet fully resolved. The goal of this paper is complementary to this line of work; we want to understand the stability of the recovery problem in the cases when efficient recovery is possible. Numerical stability of Pearl's notion of causality was first studied in Schulman and Srivastava (2016) using the concept of condition number where they provide ill-conditioned examples. In this work, we provide a condition number analysis for the $\LSEM$. First we prove that under a sufficient condition, for a certain sub-class of $\LSEM$ that are \emph{bow-free} (Brito and Pearl (2002)), the parameter recovery is stable. We further prove that \emph{randomly} chosen input parameters for this family satisfy the condition with a substantial probability. Hence for this family, on a large subset of parameter space, recovery is numerically stable. Next we construct an example of $\LSEM$ on four vertices with \emph{unbounded} condition number. We then corroborate our theoretical findings via simulations as well as real-world experiments for a sociology application. Finally, we provide a general heuristic for estimating the condition number of any $\LSEM$ instance.
HyperGCN: Hypergraph Convolutional Networks for Semi-Supervised Classification
Sep 07, 2018
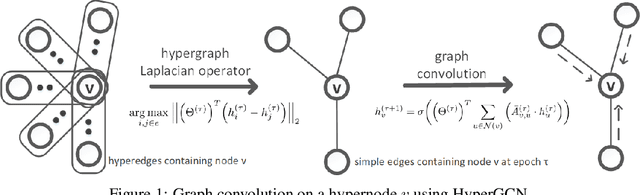

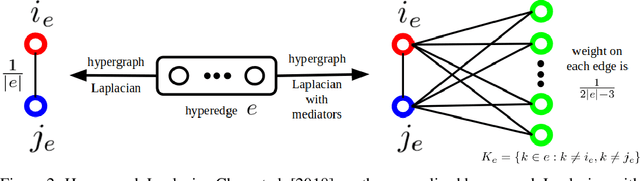
Abstract:Graph-based semi-supervised learning (SSL) is an important learning problem where the goal is to assign labels to initially unlabeled nodes in a graph. Graph Convolutional Networks (GCNs) have recently been shown to be effective for graph-based SSL problems. GCNs inherently assume existence of pairwise relationships in the graph-structured data. However, in many real-world problems, relationships go beyond pairwise connections and hence are more complex. Hypergraphs provide a natural modeling tool to capture such complex relationships. In this work, we explore the use of GCNs for hypergraph-based SSL. In particular, we propose HyperGCN, an SSL method which uses a layer-wise propagation rule for convolutional neural networks operating directly on hypergraphs. To the best of our knowledge, this is the first principled adaptation of GCNs to hypergraphs. HyperGCN is able to encode both the hypergraph structure and hypernode features in an effective manner. Through detailed experimentation, we demonstrate HyperGCN's effectiveness at hypergraph-based SSL.
On Euclidean $k$-Means Clustering with $α$-Center Proximity
Sep 06, 2018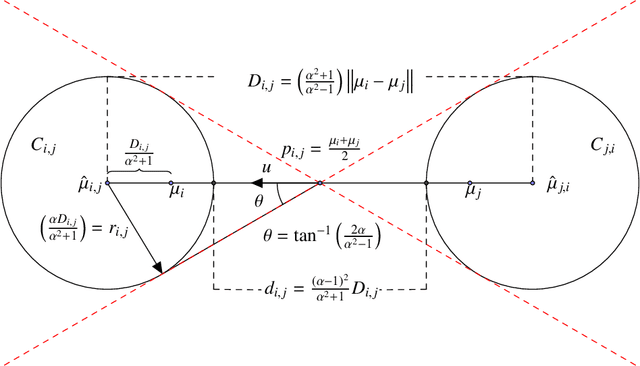
Abstract:The $k$-means is a popular clustering objective that is NP-hard in the worst-case but often solved efficiently by simple heuristics in practice. The implicit assumption behind using the $k$-means (or many other objectives) is that an optimal solution would recover the underlying ground truth clustering. In most real-world datasets, the underlying ground-truth clustering is unambiguous and stable under small perturbations of data. As a consequence, the ground-truth clustering satisfies center proximity, that is, every point is closer to the center of its own cluster than the center of any other cluster, by some multiplicative factor $\alpha > 1$. We study the problem of minimizing the Euclidean $k$-means objective only over clusterings that satisfy $\alpha$-center proximity. We give a simple algorithm to find an exact optimal clustering for the above objective with running time exponential in $k$ and $1/(\alpha - 1)$ but linear in the number of points and the dimension. We define an analogous $\alpha$-center proximity condition for outliers, and give similar algorithmic guarantees for $k$-means with outliers and $\alpha$-center proximity. On the hardness side we show that for any $\alpha' > 1$, there exists an $\alpha \leq \alpha'$, $(\alpha >1)$, and an $\varepsilon_0 > 0$ such that minimizing the $k$-means objective over clusterings that satisfy $\alpha$-center proximity is NP-hard to approximate within a multiplicative $(1+\varepsilon_0)$ factor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge