Periodic agent-state based Q-learning for POMDPs

The standard approach for Partially Observable Markov Decision Processes (POMDPs) is to convert them to a fully observed belief-state MDP. However, the belief state depends on the system model and is therefore not viable in reinforcement learning (RL) settings. A widely used alternative is to use an agent state, which is a model-free, recursively updateable function of the observation history. Examples include frame stacking and recurrent neural networks. Since the agent state is model-free, it is used to adapt standard RL algorithms to POMDPs. However, standard RL algorithms like Q-learning learn a stationary policy. Our main thesis that we illustrate via examples is that because the agent state does not satisfy the Markov property, non-stationary agent-state based policies can outperform stationary ones. To leverage this feature, we propose PASQL (periodic agent-state based Q-learning), which is a variant of agent-state-based Q-learning that learns periodic policies. By combining ideas from periodic Markov chains and stochastic approximation, we rigorously establish that PASQL converges to a cyclic limit and characterize the approximation error of the converged periodic policy. Finally, we present a numerical experiment to highlight the salient features of PASQL and demonstrate the benefit of learning periodic policies over stationary policies.

Approximate information state based convergence analysis of recurrent Q-learning

In spite of the large literature on reinforcement learning (RL) algorithms for partially observable Markov decision processes (POMDPs), a complete theoretical understanding is still lacking. In a partially observable setting, the history of data available to the agent increases over time so most practical algorithms either truncate the history to a finite window or compress it using a recurrent neural network leading to an agent state that is non-Markovian. In this paper, it is shown that in spite of the lack of the Markov property, recurrent Q-learning (RQL) converges in the tabular setting. Moreover, it is shown that the quality of the converged limit depends on the quality of the representation which is quantified in terms of what is known as an approximate information state (AIS). Based on this characterization of the approximation error, a variant of RQL with AIS losses is presented. This variant performs better than a strong baseline for RQL that does not use AIS losses. It is demonstrated that there is a strong correlation between the performance of RQL over time and the loss associated with the AIS representation.

Dealing With Non-stationarity in Decentralized Cooperative Multi-Agent Deep Reinforcement Learning via Multi-Timescale Learning

Decentralized cooperative multi-agent deep reinforcement learning (MARL) can be a versatile learning framework, particularly in scenarios where centralized training is either not possible or not practical. One of the key challenges in decentralized deep MARL is the non-stationarity of the learning environment when multiple agents are learning concurrently. A commonly used and efficient scheme for decentralized MARL is independent learning in which agents concurrently update their policies independent of each other. We first show that independent learning does not always converge, while sequential learning where agents update their policies one after another in a sequence is guaranteed to converge to an agent-by-agent optimal solution. In sequential learning, when one agent updates its policy, all other agent's policies are kept fixed, alleviating the challenge of non-stationarity due to concurrent updates in other agents' policies. However, it can be slow because only one agent is learning at any time. Therefore it might also not always be practical. In this work, we propose a decentralized cooperative MARL algorithm based on multi-timescale learning. In multi-timescale learning, all agents learn concurrently, but at different learning rates. In our proposed method, when one agent updates its policy, other agents are allowed to update their policies as well, but at a slower rate. This speeds up sequential learning, while also minimizing non-stationarity caused by other agents updating concurrently. Multi-timescale learning outperforms state-of-the-art decentralized learning methods on a set of challenging multi-agent cooperative tasks in the epymarl (papoudakis2020) benchmark. This can be seen as a first step towards more general decentralized cooperative deep MARL methods based on multi-timescale learning.

Approximate information state for approximate planning and reinforcement learning in partially observed systems

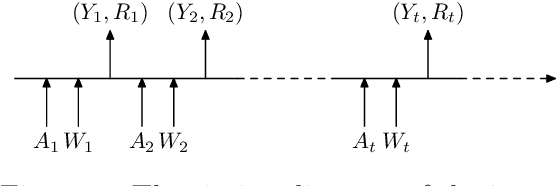
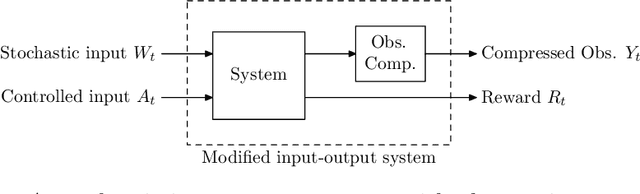
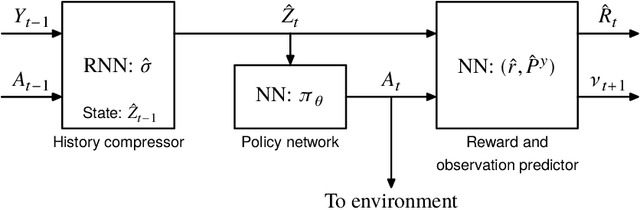
We propose a theoretical framework for approximate planning and learning in partially observed systems. Our framework is based on the fundamental notion of information state. We provide two equivalent definitions of information state---i) a function of history which is sufficient to compute the expected reward and predict its next value; ii) equivalently, a function of the history which can be recursively updated and is sufficient to compute the expected reward and predict the next observation. An information state always leads to a dynamic programming decomposition. Our key result is to show that if a function of the history (called approximate information state (AIS)) approximately satisfies the properties of the information state, then there is a corresponding approximate dynamic program. We show that the policy computed using this is approximately optimal with bounded loss of optimality. We show that several approximations in state, observation and action spaces in literature can be viewed as instances of AIS. In some of these cases, we obtain tighter bounds. A salient feature of AIS is that it can be learnt from data. We present AIS based multi-time scale policy gradient algorithms. and detailed numerical experiments with low, moderate and high dimensional environments.