BubbleONet: A Physics-Informed Neural Operator for High-Frequency Bubble Dynamics

This paper introduces BubbleONet, an operator learning model designed to map pressure profiles from an input function space to corresponding bubble radius responses. BubbleONet is built upon the physics-informed deep operator network (PI-DeepONet) framework, leveraging DeepONet's powerful universal approximation capabilities for operator learning alongside the robust physical fidelity provided by the physics-informed neural networks. To mitigate the inherent spectral bias in deep learning, BubbleONet integrates the Rowdy adaptive activation function, enabling improved representation of high-frequency features. The model is evaluated across various scenarios, including: (1) Rayleigh-Plesset equation based bubble dynamics with a single initial radius, (2) Keller-Miksis equation based bubble dynamics with a single initial radius, and (3) Keller-Miksis equation based bubble dynamics with multiple initial radii. Moreover, the performance of single-step versus two-step training techniques for BubbleONet is investigated. The results demonstrate that BubbleONet serves as a promising surrogate model for simulating bubble dynamics, offering a computationally efficient alternative to traditional numerical solvers.

Anant-Net: Breaking the Curse of Dimensionality with Scalable and Interpretable Neural Surrogate for High-Dimensional PDEs

High-dimensional partial differential equations (PDEs) arise in diverse scientific and engineering applications but remain computationally intractable due to the curse of dimensionality. Traditional numerical methods struggle with the exponential growth in computational complexity, particularly on hypercubic domains, where the number of required collocation points increases rapidly with dimensionality. Here, we introduce Anant-Net, an efficient neural surrogate that overcomes this challenge, enabling the solution of PDEs in high dimensions. Unlike hyperspheres, where the internal volume diminishes as dimensionality increases, hypercubes retain or expand their volume (for unit or larger length), making high-dimensional computations significantly more demanding. Anant-Net efficiently incorporates high-dimensional boundary conditions and minimizes the PDE residual at high-dimensional collocation points. To enhance interpretability, we integrate Kolmogorov-Arnold networks into the Anant-Net architecture. We benchmark Anant-Net's performance on several linear and nonlinear high-dimensional equations, including the Poisson, Sine-Gordon, and Allen-Cahn equations, demonstrating high accuracy and robustness across randomly sampled test points from high-dimensional space. Importantly, Anant-Net achieves these results with remarkable efficiency, solving 300-dimensional problems on a single GPU within a few hours. We also compare Anant-Net's results for accuracy and runtime with other state-of-the-art methods. Our findings establish Anant-Net as an accurate, interpretable, and scalable framework for efficiently solving high-dimensional PDEs.

Large Language Model-Based Evolutionary Optimizer: Reasoning with elitism

Large Language Models (LLMs) have demonstrated remarkable reasoning abilities, prompting interest in their application as black-box optimizers. This paper asserts that LLMs possess the capability for zero-shot optimization across diverse scenarios, including multi-objective and high-dimensional problems. We introduce a novel population-based method for numerical optimization using LLMs called Language-Model-Based Evolutionary Optimizer (LEO). Our hypothesis is supported through numerical examples, spanning benchmark and industrial engineering problems such as supersonic nozzle shape optimization, heat transfer, and windfarm layout optimization. We compare our method to several gradient-based and gradient-free optimization approaches. While LLMs yield comparable results to state-of-the-art methods, their imaginative nature and propensity to hallucinate demand careful handling. We provide practical guidelines for obtaining reliable answers from LLMs and discuss method limitations and potential research directions.

RiemannONets: Interpretable Neural Operators for Riemann Problems

Developing the proper representations for simulating high-speed flows with strong shock waves, rarefactions, and contact discontinuities has been a long-standing question in numerical analysis. Herein, we employ neural operators to solve Riemann problems encountered in compressible flows for extreme pressure jumps (up to $10^{10}$ pressure ratio). In particular, we first consider the DeepONet that we train in a two-stage process, following the recent work of Lee and Shin, wherein the first stage, a basis is extracted from the trunk net, which is orthonormalized and subsequently is used in the second stage in training the branch net. This simple modification of DeepONet has a profound effect on its accuracy, efficiency, and robustness and leads to very accurate solutions to Riemann problems compared to the vanilla version. It also enables us to interpret the results physically as the hierarchical data-driven produced basis reflects all the flow features that would otherwise be introduced using ad hoc feature expansion layers. We also compare the results with another neural operator based on the U-Net for low, intermediate, and very high-pressure ratios that are very accurate for Riemann problems, especially for large pressure ratios, due to their multiscale nature but computationally more expensive. Overall, our study demonstrates that simple neural network architectures, if properly pre-trained, can achieve very accurate solutions of Riemann problems for real-time forecasting.

Deep smoothness WENO scheme for two-dimensional hyperbolic conservation laws: A deep learning approach for learning smoothness indicators

In this paper, we introduce an improved version of the fifth-order weighted essentially non-oscillatory (WENO) shock-capturing scheme by incorporating deep learning techniques. The established WENO algorithm is improved by training a compact neural network to adjust the smoothness indicators within the WENO scheme. This modification enhances the accuracy of the numerical results, particularly near abrupt shocks. Unlike previous deep learning-based methods, no additional post-processing steps are necessary for maintaining consistency. We demonstrate the superiority of our new approach using several examples from the literature for the two-dimensional Euler equations of gas dynamics. Through intensive study of these test problems, which involve various shocks and rarefaction waves, the new technique is shown to outperform traditional fifth-order WENO schemes, especially in cases where the numerical solutions exhibit excessive diffusion or overshoot around shocks.

A unified scalable framework for causal sweeping strategies for Physics-Informed Neural Networks (PINNs) and their temporal decompositions

Physics-informed neural networks (PINNs) as a means of solving partial differential equations (PDE) have garnered much attention in Computational Science and Engineering (CS&E). However, a recent topic of interest is exploring various training (i.e., optimization) challenges - in particular, arriving at poor local minima in the optimization landscape results in a PINN approximation giving an inferior, and sometimes trivial, solution when solving forward time-dependent PDEs with no data. This problem is also found in, and in some sense more difficult, with domain decomposition strategies such as temporal decomposition using XPINNs. To address this problem, we first enable a general categorization for previous causality methods, from which we identify a gap in the previous approaches. We then furnish examples and explanations for different training challenges, their cause, and how they relate to information propagation and temporal decomposition. We propose a solution to fill this gap by reframing these causality concepts into a generalized information propagation framework in which any prior method or combination of methods can be described. Our unified framework moves toward reducing the number of PINN methods to consider and the implementation and retuning cost for thorough comparisons. We propose a new stacked-decomposition method that bridges the gap between time-marching PINNs and XPINNs. We also introduce significant computational speed-ups by using transfer learning concepts to initialize subnetworks in the domain and loss tolerance-based propagation for the subdomains. We formulate a new time-sweeping collocation point algorithm inspired by the previous PINNs causality literature, which our framework can still describe, and provides a significant computational speed-up via reduced-cost collocation point segmentation. Finally, we provide numerical results on baseline PDE problems.

Learning stiff chemical kinetics using extended deep neural operators

We utilize neural operators to learn the solution propagator for the challenging chemical kinetics equation. Specifically, we apply the deep operator network (DeepONet) along with its extensions, such as the autoencoder-based DeepONet and the newly proposed Partition-of-Unity (PoU-) DeepONet to study a range of examples, including the ROBERS problem with three species, the POLLU problem with 25 species, pure kinetics of the syngas skeletal model for $CO/H_2$ burning, which contains 11 species and 21 reactions and finally, a temporally developing planar $CO/H_2$ jet flame (turbulent flame) using the same syngas mechanism. We have demonstrated the advantages of the proposed approach through these numerical examples. Specifically, to train the DeepONet for the syngas model, we solve the skeletal kinetic model for different initial conditions. In the first case, we parametrize the initial conditions based on equivalence ratios and initial temperature values. In the second case, we perform a direct numerical simulation of a two-dimensional temporally developing $CO/H_2$ jet flame. Then, we initialize the kinetic model by the thermochemical states visited by a subset of grid points at different time snapshots. Stiff problems are computationally expensive to solve with traditional stiff solvers. Thus, this work aims to develop a neural operator-based surrogate model to solve stiff chemical kinetics. The operator, once trained offline, can accurately integrate the thermochemical state for arbitrarily large time advancements, leading to significant computational gains compared to stiff integration schemes.

Augmented Physics-Informed Neural Networks (APINNs): A gating network-based soft domain decomposition methodology

In this paper, we propose the augmented physics-informed neural network (APINN), which adopts soft and trainable domain decomposition and flexible parameter sharing to further improve the extended PINN (XPINN) as well as the vanilla PINN methods. In particular, a trainable gate network is employed to mimic the hard decomposition of XPINN, which can be flexibly fine-tuned for discovering a potentially better partition. It weight-averages several sub-nets as the output of APINN. APINN does not require complex interface conditions, and its sub-nets can take advantage of all training samples rather than just part of the training data in their subdomains. Lastly, each sub-net shares part of the common parameters to capture the similar components in each decomposed function. Furthermore, following the PINN generalization theory in Hu et al. [2021], we show that APINN can improve generalization by proper gate network initialization and general domain & function decomposition. Extensive experiments on different types of PDEs demonstrate how APINN improves the PINN and XPINN methods. Specifically, we present examples where XPINN performs similarly to or worse than PINN, so that APINN can significantly improve both. We also show cases where XPINN is already better than PINN, so APINN can still slightly improve XPINN. Furthermore, we visualize the optimized gating networks and their optimization trajectories, and connect them with their performance, which helps discover the possibly optimal decomposition. Interestingly, if initialized by different decomposition, the performances of corresponding APINNs can differ drastically. This, in turn, shows the potential to design an optimal domain decomposition for the differential equation problem under consideration.

How important are activation functions in regression and classification? A survey, performance comparison, and future directions

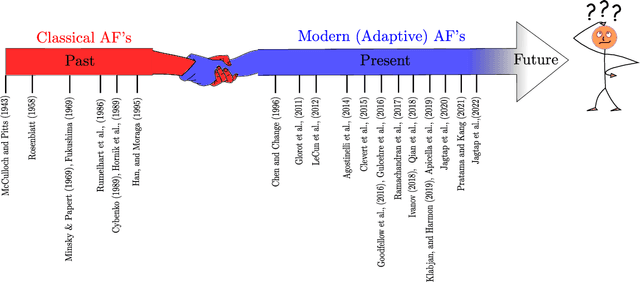
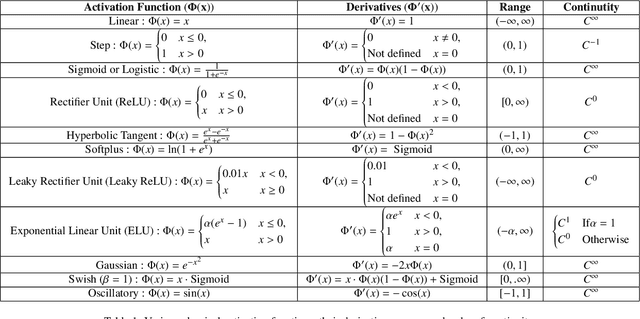
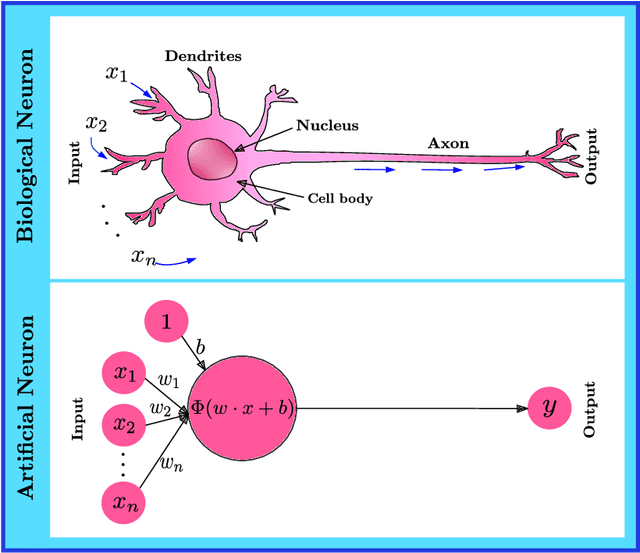
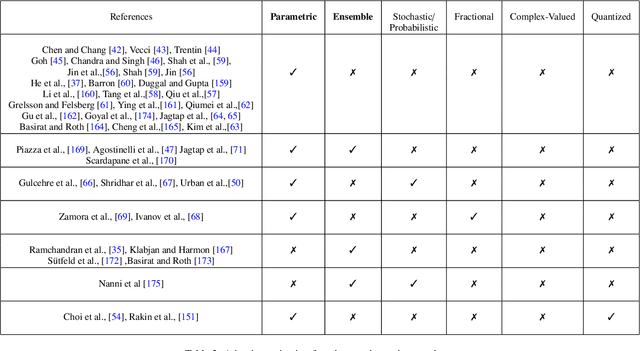
Inspired by biological neurons, the activation functions play an essential part in the learning process of any artificial neural network commonly used in many real-world problems. Various activation functions have been proposed in the literature for classification as well as regression tasks. In this work, we survey the activation functions that have been employed in the past as well as the current state-of-the-art. In particular, we present various developments in activation functions over the years and the advantages as well as disadvantages or limitations of these activation functions. We also discuss classical (fixed) activation functions, including rectifier units, and adaptive activation functions. In addition to presenting the taxonomy of activation functions based on characterization, a taxonomy of activation functions based on applications is also presented. To this end, the systematic comparison of various fixed and adaptive activation functions is performed for classification data sets such as the MNIST, CIFAR-10, and CIFAR-100. In recent years, a physics-informed machine learning framework has emerged for solving problems related to scientific computations. To this purpose, we also discuss various requirements for activation functions that have been used in the physics-informed machine learning framework. Furthermore, various comparisons are made among different fixed and adaptive activation functions using various machine learning libraries such as TensorFlow, Pytorch, and JAX.

Error estimates for physics informed neural networks approximating the Navier-Stokes equations

We prove rigorous bounds on the errors resulting from the approximation of the incompressible Navier-Stokes equations with (extended) physics informed neural networks. We show that the underlying PDE residual can be made arbitrarily small for tanh neural networks with two hidden layers. Moreover, the total error can be estimated in terms of the training error, network size and number of quadrature points. The theory is illustrated with numerical experiments.