Data-Driven Probabilistic Evaluation of Logic Properties with PAC-Confidence on Mealy Machines

Cyber-Physical Systems (CPS) are complex systems that require powerful models for tasks like verification, diagnosis, or debugging. Often, suitable models are not available and manual extraction is difficult. Data-driven approaches then provide a solution to, e.g., diagnosis tasks and verification problems based on data collected from the system. In this paper, we consider CPS with a discrete abstraction in the form of a Mealy machine. We propose a data-driven approach to determine the safety probability of the system on a finite horizon of n time steps. The approach is based on the Probably Approximately Correct (PAC) learning paradigm. Thus, we elaborate a connection between discrete logic and probabilistic reachability analysis of systems, especially providing an additional confidence on the determined probability. The learning process follows an active learning paradigm, where new learning data is sampled in a guided way after an initial learning set is collected. We validate the approach with a case study on an automated lane-keeping system.

Data-Driven Verification under Signal Temporal Logic Constraints

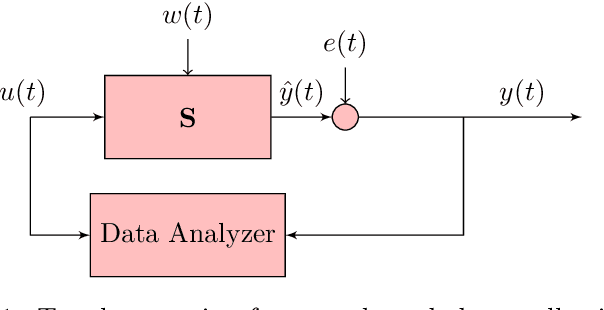
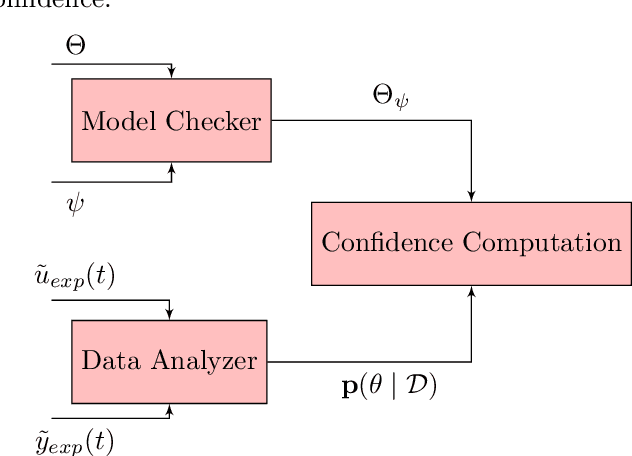
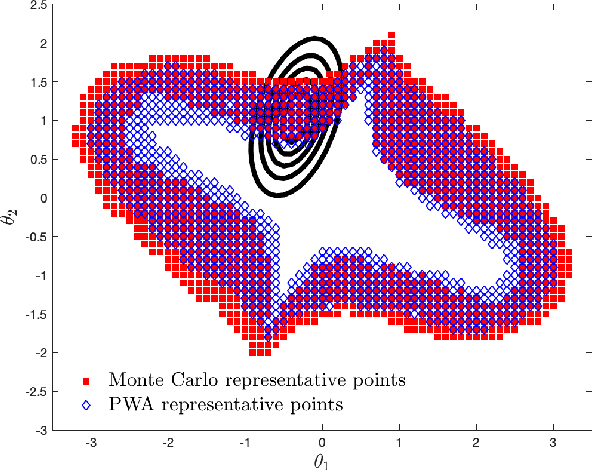
We consider systems under uncertainty whose dynamics are partially unknown. Our aim is to study satisfaction of temporal logic properties by trajectories of such systems. We express these properties as signal temporal logic formulas and check if the probability of satisfying the property is at least a given threshold. Since the dynamics are parameterized and partially unknown, we collect data from the system and employ Bayesian inference techniques to associate a confidence value to the satisfaction of the property. The main novelty of our approach is to combine both data-driven and model-based techniques in order to have a two-layer probabilistic reasoning over the behavior of the system: one layer is related to the stochastic noise inside the system and the next layer is related to the noisy data collected from the system. We provide approximate algorithms for computing the confidence for linear dynamical systems.